八年级下册第十七章 勾股定理17.1 勾股定理教学ppt课件

这是一份八年级下册第十七章 勾股定理17.1 勾股定理教学ppt课件，共19页。PPT课件主要包含了导入新课，勾股定理的概念，探究新知，小于AC即可，知识归纳，4解决实际问题，数学问题，直角三角形，勾股定理，实际问题等内容，欢迎下载使用。

在任何一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。
在△ABC中，∠C=90°，则a²+b²=c²
1. 在Rt△ABC中，∠A，∠B，∠C的对边为a，b，c， ∠C＝90°.
(1)已知a＝3，b＝4，则c＝______；
(2)已知c＝25，b＝15，则a＝_______；
(3)已知c＝19，a＝13，则b＝_______；(结果保留根号)
(4)已知a∶b＝3∶4，c＝15，则b＝______．
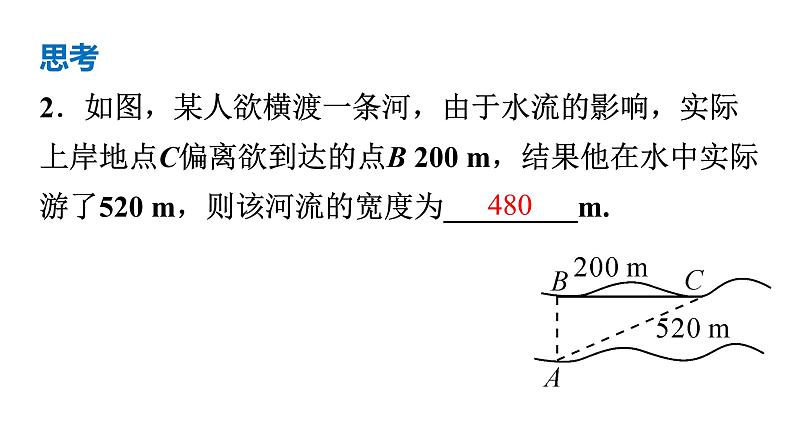
2．如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达的点B 200 m，结果他在水中实际游了520 m，则该河流的宽度为_________m.
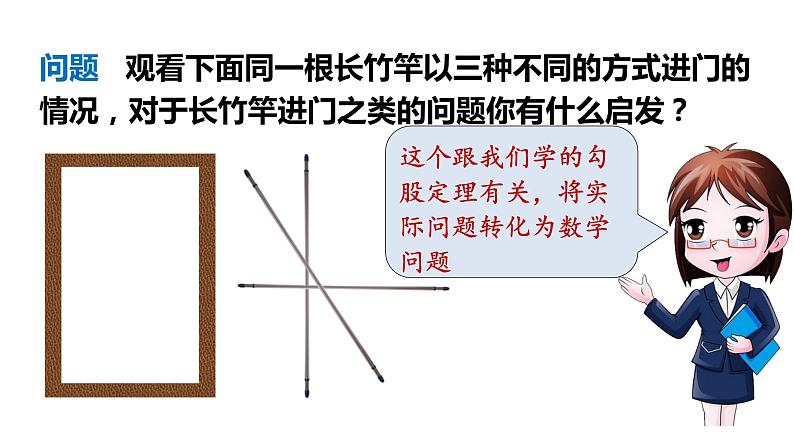
问题 观看下面同一根长竹竿以三种不同的方式进门的情况，对于长竹竿进门之类的问题你有什么启发？
这个跟我们学的勾股定理有关，将实际问题转化为数学问题
一个门框的尺寸如图所示，一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
（1）木板能横着或竖着从门框通过吗？
（2）这个门框能通过的最大长度是多少？
（3）怎样判定这块木板能否通过木框？
求出斜边的长，与木板的宽比较.
解：在Rt△ABC中，根据勾股定理，
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
利用勾股定理解决实际问题的一般步骤：
（1）读懂题意，分析已知、未知间的关系；
（2）构造直角三角形；
（3）利用勾股定理等列方程；
解：在Rt△AOB中，根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1，
在Rt△COD中，根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时，梯子底端并不是也外移0.5m，而是外移约0.77m.
例1 如图，一架2.6m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
例2　如图，在一棵树的10 m高的B处有两只猴子，其中一只猴子爬下树，走到离树20 m处的池塘A处，另一只猴子爬到树顶D后直接跃向池塘A处(假设它经过的路线为直线)，如果两只猴子所经过的路程相等，求这棵树的高．
由题意知，BC＋AC＝BD＋AD，
∴AD＝(30－x)m.
在Rt△ACD中，由勾股定理，得
(10＋x)2＋202＝(30－x)2，解得x＝5，
∴x＋10＝5＋10＝15.
答：这棵树高15 m.
例3　如图，长方体的长BE＝15 cm，宽AB＝10 cm，高AD＝20 cm，点M在CH上，且CM＝5 cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点M，需要爬行的最短距离是多少？
解：分两种情况比较最短距离：
如答图①所示，蚂蚁爬行的最短路线为AM，
答：需要爬行的最短距离是25 cm.
∴第二种路线较短，此时最短距离为25 cm.
立体图形中求两点间的最短距离，一般把立体图形展开成平面图形，连接两点，根据两点之间线段最短确定最短路线.
如答图②所示，蚂蚁爬行的最短路线为AM，
应用勾股定理的前提是在________三角形中．如果三角形不是直角三角形，要先_________________，再利用勾股定理求未知边的长．
①在直角三角形中，已知两边长，利用勾股定理求第三边时，要弄清楚直角边和斜边，没有明确规定时，要__________，以免漏解；
②求几何体表面上两点间的最短距离的方法：把立体图形的表面展开成平面图形，根据“两点之间，______最短”确定路径，然后利用勾股定理进行计算；
③用勾股定理解决折叠问题时，能够重合的线段、角和面积______．
1.如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上一点，测得BC=60 m，AC=20m.求A，B两点间的距离（结果取整数）.
2.如图，在平面直角坐标系中有两点A(5，0)和B(0，4)，求这两点间的距离.
解：在Rt△AOB中，
∴AB2＝OA2+OB2＝52+42＝41,
∵OA=5，OB=4,
4．如图，牧童在A处放牛，牧童家在B处，A，B处距河岸的距离AC，BD分别为500 m和300 m，且C，D两处的距离为600 m，天黑前牧童从A处将牛牵到河边去饮水，再赶回家，那么牧童最少要走多少米？
解：如图，作点B关于CD的对称点B′，连接AB′，交CD于点P，
答：牧童最少要走1 000 m.
过点A作B′B的垂线，垂足为E.
在Rt△AB′E中，AE＝600 m，B′E＝800 m，