初中数学冀教版八年级下册第二十一章 一次函数综合与测试练习

这是一份初中数学冀教版八年级下册第二十一章 一次函数综合与测试练习，共27页。试卷主要包含了已知点等内容，欢迎下载使用。
八年级数学下册第二十一章一次函数专项练习
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、下列函数中，y是x的一次函数的是（　　）
A．y＝ B．y＝﹣3x+1 C．y＝2 D．y＝x2+1
2、如图，在平面直角坐标系中，，，，点D在线段BA上，点E在线段BA的延长线上，并且满足，M为线段AC上一点，当点D、M、E构成以M为直角顶点的等腰直角三角形时，M点坐标为（ ）

A． B． C． D．
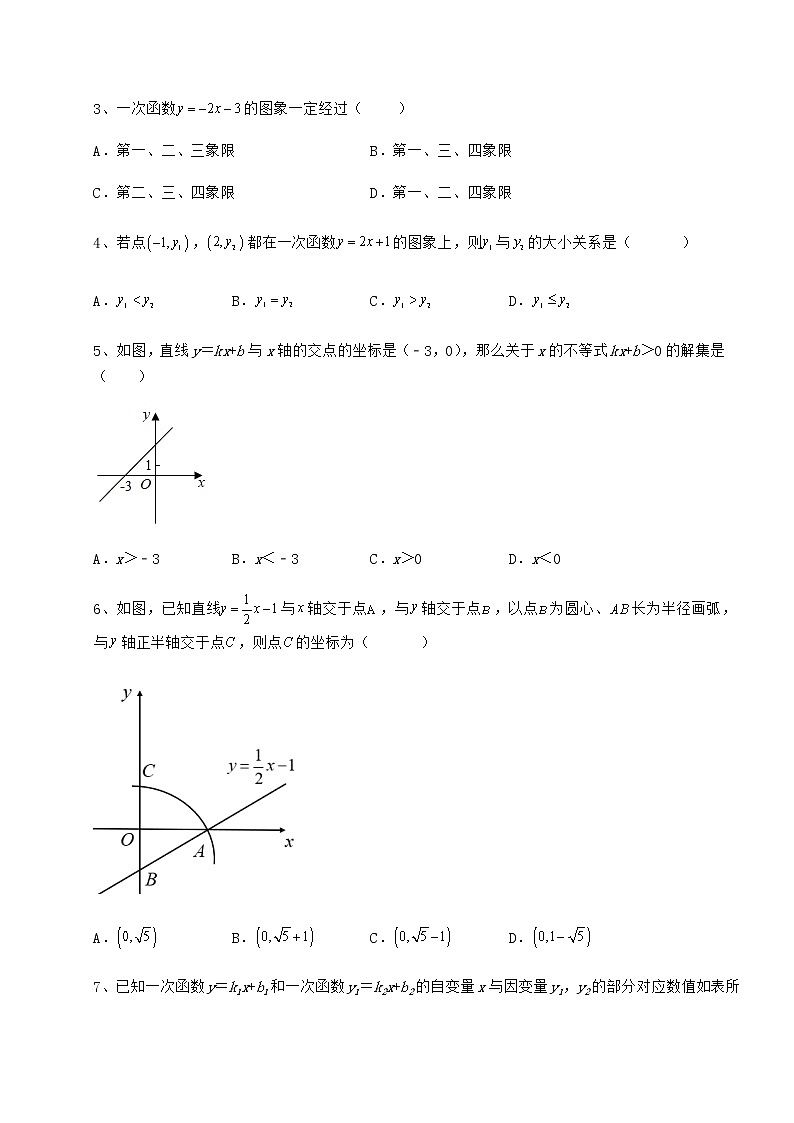
3、一次函数的图象一定经过（ ）
A．第一、二、三象限 B．第一、三、四象限
C．第二、三、四象限 D．第一、二、四象限
4、若点，都在一次函数的图象上，则与的大小关系是（ ）
A． B． C． D．
5、如图，直线y＝kx+b与x轴的交点的坐标是（﹣3，0），那么关于x的不等式kx+b＞0的解集是（　　）

A．x＞﹣3 B．x＜﹣3 C．x＞0 D．x＜0
6、如图，已知直线与轴交于点，与轴交于点，以点为圆心、长为半径画弧，与轴正半轴交于点，则点的坐标为（ ）

A． B． C． D．
7、已知一次函数y＝k1x+b1和一次函数y1＝k2x+b2的自变量x与因变量y1，y2的部分对应数值如表所示，则关于x、y的二元一次方程组的解为（　　）
x
…
﹣2
﹣1
0
1
2
…
y1
…
﹣1
0
1
2
3
…
y2
…
﹣5
﹣3
﹣1
1
3
…
A． B． C． D．
8、一次函数y1＝kx+b与y2＝mx+n的部分自变量和对应函数值如表：
x
…
﹣2
﹣1
0
1
2
…
y1
…
1
2
3
4
5
…

x
…
﹣2
﹣1
0
1
2
…
y2
…
5
2
﹣1
﹣4
﹣7
…
则关于x的不等式kx+b＞mx+n的解集是（　　）
A．x＞0 B．x＜0 C．x＜﹣1 D．x＞﹣1
9、已知点（﹣1，y1），（4，y2）在一次函数y＝3x+a的图象上，则y1，y2的大小关系是（　　）
A．y1＜y2 B．y1＝y2 C．y1＞y2 D．不能确定
10、若直线y＝kx＋b经过一、二、四象限，则直线y＝bx﹣k的图象只能是图中的（ ）
A． B． C． D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、 “”是一款数学应用软件，用“”绘制的函数和的图像如图所示．若，分别为方程和的一个解，则根据图像可知____．（填“”、“”或“”）．

2、一般地，形如y＝kx＋b（k≠0，k、b为常数）的函数，叫做______函数．注意：k是常数，k≠0，k可以是正数、也可以是负数；b可以取______ ．
3、如图，将正方形置于平面直角坐标系中，其中，，边在轴上，直线与正方形的边有两个交点、，当时，的取值范围是__．

4、函数和的图象相交于点，则方程的解为______．

5、在弹性限度内，弹簧的长度 y（厘米）是所挂物体质量 x（千克）的一次函数．一根弹簧不挂物体时长14.5厘米；当所挂物体的质量为3千克时，弹簧长16厘米．请写出 y 与x之间的关系式，并求当所挂物体的质量为4千克时弹簧的长度．
解：设y＝kx＋b（k≠0）
由题意得：14.5＝b，
16＝3k＋b，
解得：b＝___，k＝___．
所以在弹性限度内，___，
当x＝4时，y＝0.5×4＋14.5＝___（厘米）．
即物体的质量为4千克时，弹簧长度为16.5厘米．
三、解答题（5小题，每小题10分，共计50分）
1、某单位要制作一批宣传材料，甲公司提出：每份材料收费25元，另收2000元的设计费；乙公司提出：每份材料收费35元，不收设计费．
(1)请用含x代数式分别表示甲乙两家公司制作宣传材料的费用；
(2)试比较哪家公司更优惠？说明理由．
2、已知一次函数在轴上的截距为2，且随的增大而减小，求一次函数的解析式，并求出它的图像与坐标轴围成的三角形的面积
3、在平面直角坐标系xOy中，对于线段AB和点C，若△ABC是以AB为一条直角边，且满足AC>AB的直角三角形，则称点C为线段AB的“关联点”，已知点A的坐标为（0，1）．

(1)若B（2，1），则点D（3，1），E（2，0），F（0，-3），G（-1，-2）中，是AB关联点的有_______；
(2)若点B（-1，0），点P在直线y=2x-3上，且点P为线段AB的关联点，求点P的坐标；
(3)若点B（b，0）为x轴上一动点，在直线y=2x+2上存在两个AB的关联点，求b的取值范围．
4、一次函数y=kx+b，当-3≤x≤1时，对应的y的取值为1≤y≤9，求该函数的解析式．
5、已知一次函数图象与直线平行且过点．
(1)求一次函数解析式；
(2)若（1）中一次函数图象，分别与、轴交于、两点，求、两点坐标；
(3)若点在轴上，且，求点坐标．

-参考答案-
一、单选题
1、B
【解析】
【分析】
利用一般地，形如y=kx+b（k≠0，k、b是常数）的函数，叫做一次函数，进而判断得出答案．
【详解】
解：∵y＝不符合一次函数的形式，故不是一次函数，
∴选项A不符合题意；
∵形如y＝kx+b（k，b为常数）．
∴y＝﹣3x+1中，y是x的一次函数．
故选项B符合题意；
∵y＝2是常数函数，
∴选项C不符合题意；
∵y＝x2+1不符合一次函数的形式，故不是一次函数，
∴选项D不符合题意；
综上，y是x的一次函数的是选项B．
故选：B．
【点睛】
本题主要考查了一次函数的定义，正确把握一次函数的定义是解题关键．
2、A
【解析】
【分析】
过点M作y轴的平行线，过点E、D分别作这条直线的垂线，垂足分别为F、G，求出直线AB、AC的解析式，设出点D、E、M的坐标，根据△DGM≌△MFE，建立方程求解即可．
【详解】
解：过点M作y轴的平行线，过点E、D分别作这条直线的垂线，垂足分别为F、G，
设直线AB的解析式为，把，代入得，
，解得，，
∴AB的解析式为，
同理可求直线AC的解析式为，
设点D坐标为，点M坐标为，
∵，
∴
∵，，
∴点E是由点D向右平移3个单位，向上平移9个单位得到的，则点E坐标为，
∵∠EFM=∠DGM=∠DME
∴∠FEM+∠FME=∠DMG+∠FME =90°，
∴∠FEM =∠DMG，
∵DM=EM，
∴△DGM≌△MFE，
∴DG=FM，GM=EF，
根据坐标可列方程组，b-a=3a+18+1.5b-9-1.5b+9-3a-9=b-a-3，
解得，，
所以，点M坐标为，
故选：A．

【点睛】
本题考查了求一次函数解析式和全等三角形的判定与性质，解题关键是求出直线解析式，设出点的坐标，利用全等三角形建立方程．
3、C
【解析】
【分析】
k＜0，函数一定经过第二，四象限，b＜0，直线与y轴交于负半轴，所以函数图象过第三象限．
【详解】
解：∵k=-2＜0，b=-3＜0，
∴函数的图象经过第二、三、四象限，
故选：C．
【点睛】
本题考查了一次函数的性质，k＞0，函数一定经过第一，三象限，k＜0，函数一定经过第二，四象限，再根据直线与y轴的交点即可得出函数所过的象限，这是解题的关键．
4、A
【解析】
【分析】
根据k＞0时，y随x的增大而增大，进行判断即可．
【详解】
解：∵点，都在一次函数的图象上，
∴y随x的增大而增大


故选A
【点睛】
本题考查了一次函数的性质以及一次函数图象上点的坐标特征，解题的关键是牢记
“当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小”．
5、A
【解析】
【分析】
根据图象直接解答即可．
【详解】
∵直线y＝kx+b与x轴交点坐标为（﹣3，0），
∴由图象可知，当x＞﹣3时，y＞0，
∴不等式kx+b＞0的解集是x＞﹣3．
故选：A．
【点睛】
此题考查了一次函数图象与不等式的关系，不等式的解集即为一次函数的函数值大于零、等于零或小于零，正确理解二者之间的关系是解题的关键．
6、C
【解析】
【分析】
求出点A、点坐标，求出长即可求出点的坐标．
【详解】
解：当x=0时，，点B的坐标为（0，-1）；当y=0时，，解得，，点A的坐标为（2，0）；
即，，；
以点为圆心、长为半径画弧，与轴正半轴交于点，
故，则，
点C的坐标为；
故选：C
【点睛】
本题考查了一次函数与坐标轴交点坐标和勾股定理，解题关键是求出一次函数与坐标轴交点坐标，利用勾股定理求出线段长．
7、C
【解析】
【分析】
利用方程组的解就是两个相应的一次函数图象的交点坐标解决问题．
【详解】
解：由表格可知，一次函数y1=k1x+b1和一次函数y2=k2x+b2的图象都经过点(2，3)，
∴一次函数y1=k1x与y=k2x+b的图象的交点坐标为(2，3)，
∴关于x，y的二元一次方程组的解为．
故选：C．
【点睛】
本题考查了一次函数图像交点坐标与方程组解的关系：对于函数y1=k1x+b1，y2=k2x+b2，其图象的交点坐标(x，y)中x，y的值是方程组的解．
8、D
【解析】
【分析】
根据统计表确定两个函数的增减性以及函数的交点，然后根据增减性判断．
【详解】
解：根据表可得y1＝kx+b中y随x的增大而增大；
y2＝mx+n中y随x的增大而减小，且两个函数的交点坐标是（﹣1，2）．
则当x＞﹣1时，kx+b＞mx+n．
故选：D．
【点睛】
本题考查了一次函数与一元一次不等式，一次函数的性质，正确确定增减性以及交点坐标是关键．
9、A
【解析】
【分析】
根据一次函数y＝3x+a的一次项系数k＞0时，函数值随自变量的增大而增大的性质来求解即可．
【详解】
解：∵一次函数y＝3x+a的一次项系数为3＞0，
∴y随x的增大而增大，
∵点（﹣1，y1），（4，y2）在一次函数y＝3x+a的图象上，﹣1＜4，
∴y1＜y2，
故选：A．
【点睛】
本题考查了一次函数的性质，掌握，时，随的增大而增大是解题的关键．
10、B
【解析】
【分析】
根据直线y＝kx＋b经过一、二、四象限，可得k＜0，b＞0，从而得到直线y＝bx﹣k过一、二、三象限，即可求解．
【详解】
解：∵直线y＝kx＋b经过一、二、四象限，
∴k＜0，b＞0，
∴﹣k＞0，
∴直线y＝bx﹣k过一、二、三象限，
∴选项B中图象符合题意．
故选：B
【点睛】
本题主要考查了一次函数的图象和性质，熟练掌握一次函数的图象和性质是解题的关键．
二、填空题
1、＜
【解析】
【分析】
根据方程的解是函数图象交点的横坐标，结合图象得出结论．
【详解】
解：∵方程-x2（x-4）=-1的解为函数图象与直线y=-1的交点的横坐标，
-x+4=-1的一个解为一次函数y=-x+4与直线y=-1交点的横坐标，
如图所示：

由图象可知：a＜b．
故答案为：＜．
【点睛】
本题考查了函数图象与方程的解之间的关系，关键是利用数形结合，把方程的解转化为函数图象之间的关系．
2、 一次 任意实数
【解析】
略
3、或且
【解析】
【分析】
设BC与y轴交于点M，根据题意可得E点不在AD边上，即，分两种情况进行讨论：①如果，那么点E在AB边或线段BM上；②如果，那么点E在CD边或线段CM上；对两种情况的临界情况进行分析即可得出结果．
【详解】
解：如图，设BC与y轴交于点M，

，，，
∴E点不在AD边上，
；
①如果，那么点E在AB边或线段BM上，
当点E在AB边且时，
由勾股定理得，，
，
，，
当直线经过点，时，．
，
，
当点E在线段BM上时，，
，符合题意；
②如果，那么点E在CD边或线段CM上，
当点E在CD边且时，E与D重合；
当时，由勾股定理得，，
，
，此时E与C重合，
当直线经过点时，．
当点E在线段CM上时，，
且，符合题意；
综上，当时，的取值范围是或且，
故答案为：或且．
【点睛】
题目主要考查正比例函数的综合问题，包括其性质及分类讨论思想，勾股定理解三角形等，理解题意，熟练掌握运用分类思想是解题关键．
4、
【解析】
【分析】
由题意知，方程的解为其交点的横坐标，进而可得结果．
【详解】
解：由题意知的解为两直线交点的横坐标
故答案为：．
【点睛】
本题考查了一次函数图象的交点与一次方程解的关系．解题的关键在于理解一次函数图象的交点与一次方程解的关系．
5、 14.5 0.5 16.5
【解析】
略
三、解答题
1、 (1)y甲＝25x＋2 000；y乙＝35x
(2)当0＜x＜200时，选择乙公司更优惠；当x＝200时，选择两公司费用一样多；当x＞200时，选择甲公司更优惠．理由见解析
【解析】
【分析】
（1）设甲公司制作宣传材料的费用为y甲(元)，乙公司制作宣传材料的费用为y乙(元)，份数乘以单价加上设计费可得甲公司的费用；份数乘以单价可得乙公司的费用；
（2）分三种情况讨论，当y甲＞y乙时，当y甲＝y乙时，当y甲＜y乙时，分别计算可得
(1)
解：设甲公司制作宣传材料的费用为y甲(元)，乙公司制作宣传材料的费用为y乙(元)，制作宣传材料的份数为x(份)，
依题意得y甲＝25x＋2 000；y乙＝35x；
(2)
解：当y甲＞y乙时，即25x＋2 000＞35x，
解得：x＜200；
当y甲＝y乙时，即25x＋2 000＝35x，
解得：x＝200；
当y甲＜y乙时，即25x＋2 000＜35x，
解得：x＞200.
∴当0＜x＜200时，选择乙公司更优惠；
当x＝200时，选择两公司费用一样多；
当x＞200时，选择甲公司更优惠．
【点睛】
此题考查了一元一次方程的方案选择问题，一元一次不等式类的方案选择问题，列代数式，正确理解题意是解题的关键．
2、y=-2x+2；1
【解析】
【分析】
根据截距为2，且y随x的增大而减小即可确定k值，求出解析式即可求出面积．
【详解】
解：∵一次函数y=kx+k2-2在y轴上的截距为2，
∴|k2-2|=2，
即k=±2或k'=0，
又∵y随x的增大而减小，
∴k＜0，
即k=-2，
∴一次函数解析式为y=-2x+2；
作出函数图象如图，

设坐标轴原点为O，函数图象与x轴交于点B，与y轴交于点A，
由解析式可知A（0，2），B（1，0），
∴OA=2，OB=1，
∴S△AOB=OA•OB=×2×1=1．
【点睛】
本题主要考查一次函数的知识，熟练掌握一次函数基本知识是解题的关键．
3、 (1)点E，点F；
(2)（）或（）；
(3)b的取值范围1＜b＜2或2＜b＜3．
【解析】
【分析】
（1）根据以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，△ABE为直角三角形，且AE大于AB；以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，BF大于AB即可；
（2）根据点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，得出△AOB为等腰直角三角形，可得∠ABO=∠BAO=45°，以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，利用待定系数法求出AS解析式为，联立方程组，以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，∠OBR=90°-∠ABO=45°，可得△OBR为等腰直角三角形，OR=OB=1，点R（0，-1），利用平移的性质可求BR解析式为，联立方程组，解方程组即可；
（3）过点A与AB垂直的直线交直线y=2x+2于U，把△AOB绕点A顺时针旋转90°，得△AO′U，AO′=AO=1，O′U=OB=b，根据点U（-1，b-1）在直线上，得出方程，求出b的值，当过点A的直线与直线平行时没有 “关联点”，OB=OW=b=2，得出在1＜b＜2时，直线上存在两个AB的“关联点”，当b＞2时，根据旋转性质将△AOB绕点A逆时针旋转90°得到△AO′U，得出AO′=AO=1，O′U=OB=b，根据点U（1,1+b）在直线上，列方程，得出即可．
(1)
解：点D与AB纵坐标相同，在直线AB上，不能构成直角三角形，
以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，
∴△ABE为直角三角形，且AE大于AB；

以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，AF=4＞AB=2，

∴点E与点F是AB关联点，
点G不在A、B两点垂直的直线上，故不能构成直角三角形，
故答案为点E，点F；
(2)
解：∵点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，
∴△AOB为等腰直角三角形，AB=
∴∠ABO=∠BAO=45°，
以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，
∴∠OAS=90°-∠BAO=45°，
∴△AOS为等腰直角三角形，
∴OS=OA=1，点S（1,0），
设AS解析式为代入坐标得：
，
解得，
AS解析式为，
∴，
解得，
点P（），
AP=，AP＞AB
以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，
∴∠OBR=90°-∠ABO=45°，
∴△OBR为等腰直角三角形，
∴OR=OB=1，点R（0，-1），
过点R与AS平行的直线为AS直线向下平移2个单位，
则BR解析式为，
∴，
解得，
点P1（），
AP1=＞，
∴点P为线段AB的关联点，点P的坐标为（）或（）；

(3)
解：过点A与AB垂直的直线交直线y=2x+2于U，
把△AOB绕点A顺时针旋转90°，得△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（-1，b-1）在直线上，
∴
∴，
∴当b＞1时存在两个“关联点”，
当b＜1时，UA＜AB，不满足定义，没有两个“关联点”

当过点A的直线与直线平行时没有 “关联点”
与x轴交点X（-1，0），与y轴交点W（0，2）
∵OA=OX=1,∠XOW=∠AOB=90°，AB⊥XW，
∴△OXW顺时针旋转90°，得到△OAB，
∴OB=OW=2，
∴在1＜b＜2时，直线上存在两个AB的“关联点”，

当b＞2时，将△AOB绕点A逆时针旋转90°得到△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（1,1+b）在直线上，
∴
∴解得
∴当2＜b＜3时, 直线上存在两个AB的“关联点”，
当b＞3时，UA＜AB，不满足定义，没有两个“关联点”

综合得，b的取值范围1＜b＜2或2＜b＜3．
【点睛】
本题考查新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，掌握新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，是解题关键．
4、函数的解析式为y=2x+7或y=-2x+3
【解析】
【分析】
分类讨论：由于一次函数是递增或递减函数，所以当一次函数y=kx+b为增函数时，则x=-3，y=1；x=1，y=9，当一次函数y=kx+b为减函数时，则x=-3，y=9；x=1，y=1，然后把它们分别代入y=kx+b中得到方程组，再解两个方程组即可．
【详解】
解：当x=-3，y=1；x=1，y=9，
∴，
解方程组得；
当x=-3，y=9；x=1，y=1，
∴，
解方程组得，
∴函数的解析式为y=2x+7或y=-2x+3．
【点睛】
本题考查了待定系数法求一次函数解析式：先设一次函数的解析式为y=kx+b，然后把一次函数图象上两点的坐标代入得到关于k、b的方程组，解方程组求出k、b的值，从而确定一次函数的解析式．也考查了分类讨论思想的运用．
5、 (1)
(2)，
(3)或
【解析】
【分析】
（1）由一次函数图象平移的性质得到k=2，再将点代入求出解析式；
（2）分别求出y=0及x=0时的对应值，即可得到A、两点坐标；
（3）由结合三角形的面积公式得到AP=2AO，即可得到点P坐标．
(1)
解：设一次函数的解析式为，
一次函数图象与直线平行，
，
过点，
∴，
，
一次函数解析式为；
(2)
解：把代入得，，
，
，
把x=0代入得，，
；
(3)
解：∵，，
AP=2AO=2，
-1-2=-3，-1+2=1，
或．
【点睛】
此题考查了一次函数平移的性质，一次函数图象与坐标轴的交点坐标，一次函数与图形面积问题，正确掌握一次函数的综合知识是解题的关键．