初中数学冀教版八年级下册第二十一章 一次函数综合与测试同步达标检测题

这是一份初中数学冀教版八年级下册第二十一章 一次函数综合与测试同步达标检测题，共29页。试卷主要包含了若一次函数等内容，欢迎下载使用。
八年级数学下册第二十一章一次函数定向训练
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、在平面直角坐标系中，正比例函数y ＝kx（k＜0）的图象的大致位置只可能是（ ）
A． B．
C． D．
2、已知点和点是一次函数图象上的两点，若，则下列关于的值说法正确的是（ ）
A．一定为正数 B．一定为负数 C．一定为0 D．以上都有可能
3、在平面直角坐标系中，已知点，点，在x轴上确定点C，使得的周长最小，则点C的坐标是（ ）
A． B． C． D．
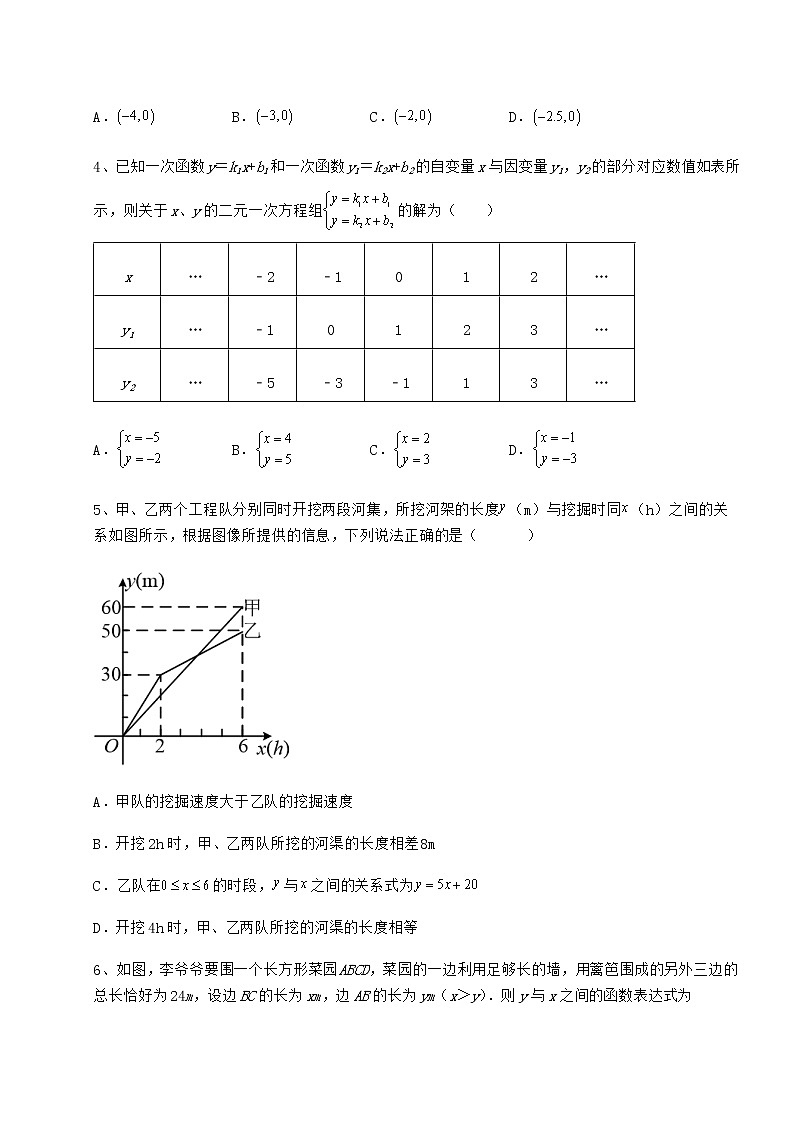
4、已知一次函数y＝k1x+b1和一次函数y1＝k2x+b2的自变量x与因变量y1，y2的部分对应数值如表所示，则关于x、y的二元一次方程组的解为（　　）
x
…
﹣2
﹣1
0
1
2
…
y1
…
﹣1
0
1
2
3
…
y2
…
﹣5
﹣3
﹣1
1
3
…
A． B． C． D．
5、甲、乙两个工程队分别同时开挖两段河集，所挖河架的长度（m）与挖掘时同（h）之间的关系如图所示，根据图像所提供的信息，下列说法正确的是（ ）

A．甲队的挖掘速度大于乙队的挖掘速度
B．开挖2h时，甲、乙两队所挖的河渠的长度相差8m
C．乙队在的时段，与之间的关系式为
D．开挖4h时，甲、乙两队所挖的河渠的长度相等
6、如图，李爷爷要围一个长方形菜园ABCD，菜园的一边利用足够长的墙，用篱笆围成的另外三边的总长恰好为24m，设边BC的长为xm，边AB的长为ym（x＞y）．则y与x之间的函数表达式为（　　）

A．y＝﹣2x+24（0＜x＜12） B．y＝﹣x+12（8＜x＜24）
C．y＝2x﹣24（0＜x＜12） D．y＝x﹣12（8＜x＜24）
7、如图，平面直角坐标系中，直线分别交x轴、y轴于点B、A，以AB为一边向右作等边，以AO为一边向左作等边，连接DC交直线l于点E．则点E的坐标为（ ）

A． B．
C． D．
8、如图，直线与x轴交于点B，与y轴交于点C，点，D为线段的中点，P为y轴上的一个动点，连接、，当的周长最小时，点P的坐标为（ ）

A． B． C． D．
9、若一次函数（，为常数，）的图象不经过第三象限，那么，应满足的条件是（ ）
A．且 B．且
C．且 D．且
10、如图，已知直线与轴交于点，与轴交于点，以点为圆心、长为半径画弧，与轴正半轴交于点，则点的坐标为（ ）

A． B． C． D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、在运用一次函数解决实际问题时，首先判断问题中的两个变量之间是不是____关系，当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果．
2、在平面直角坐标系xOy中，点A点B的坐标分别是（4，8），（12，0），则△AOB的重心G的坐标是 _____．
3、一次函数y＝﹣2x+7的图象不经过第 _____象限．
4、若一次函数y＝2x＋b的图象经过A（－1，1）则b＝____，该函数图象经过点B（1，__）和点C（___，0）．
5、如图，直线y＝kx+b交坐标轴于A，B两点，则关于x的不等式kx+b＜0的解集是_____．

三、解答题（5小题，每小题10分，共计50分）
1、某单位要制作一批宣传材料，甲公司提出：每份材料收费25元，另收2000元的设计费；乙公司提出：每份材料收费35元，不收设计费．
(1)请用含x代数式分别表示甲乙两家公司制作宣传材料的费用；
(2)试比较哪家公司更优惠？说明理由．
2、如图，在平面角坐标系中，点B在y轴的负半轴上（0，﹣2），过原点的直线OC与直线AB交于C，∠COA＝∠OCA＝∠OBA＝30°

(1)点C坐标为 　 　，OC＝　 　，△BOC的面积为 　 　，＝　 　；
(2)点C关于x轴的对称点C′的坐标为 　 　；
(3)过O点作OE⊥OC交AB于E点，则△OAE的形状为 　 　，请说明理由；
(4)在坐标平面内是否存在点F使△AOF和△AOB全等，若存在，请直接写出F坐标，请说明理由．
3、如图，已知直线l1：y=kx+2与x轴相交于点A，与y轴相交于点B，且AB=；直线l2经过点(2，2)且平行于直线y=−2x．直线l2与x轴交于点C，与y轴交于点D，与直线l1交于点N．

(1)求k的值；
(2)求四边形OCNB的面积；
(3)若线段CD上有一动点P（不含端点），过P点作x轴的垂线，垂足为M．设点P的横坐标为m．若PM≤3，求m的取值范围．
4、为巩固拓展脱贫攻坚成果，开启乡村振兴发展之门，某村村民组长组织村民加工板栗并进行销售．根据现有的原材料，预计加工规格相同的普通板栗、精品板栗共4000件．某天上午的销售件数和所卖金额统计如下表：

普通板栗（件）
精品板栗（件）
总金额（元）
甲购买情况
2
3
350
乙购买情况
4
1
300
(1)求普通板栗和精品板栗的单价分别是多少元．
(2)根据（1）中求出的单价，若普通板栗和精品板栗每件的成本分别为40元、60元，且加工普通板栗a件（），则4000件板栗的销售总利润为w元．问普通板栗和精品板栗各加工多少件，所获总利润最多？最多总利润是多少？
5、某厂计划生产A，B两种产品若干件，已知两种产品的成本价和销售价如下表：

A种产品
B种产品
成本价（元/件）
400
300
销售价（元/件）
560
450
(1)第一次工厂用220000元资金生产了A，B两种产品共600件，求两种产品各生产多少件？
(2)第二次工厂生产时，工厂规定A种产品生产数量不得超过B种产品生产数量的一半．工厂计划生产两种产品共3000件，应如何设计生产方案才能获得最大利润，最大利润是多少？

-参考答案-
一、单选题
1、A
【解析】
略
2、A
【解析】
【分析】
由 可得一次函数的性质为随的增大而增大，从而可得答案.
【详解】
解：点和点是一次函数图象上的两点，，
随的增大而增大，
即一定为正数，
故选A
【点睛】
本题考查的是一次函数的增减性的应用，掌握“一次函数，随的增大而增大， 则”是解本题的关键.
3、C
【解析】
【分析】
因为AB的长度是确定的，故△CAB的周长最小就是CA+CB的值最小，作点A关于x轴的对称点A′，连接A′B交x轴于点C，求出C点坐标即可．
【详解】
解：如图，作点A关于x轴的对称点A′，连接A′B交x轴于点C，此时，AC+BC=A′C+BC=AC，长度最小，
∵A（-1，2），
∴A′（-1，﹣2），
设直线A′B的解析式为y＝kx+b（k≠0），把A′（-1，﹣2），代入得，
∴，解得，
∴直线A′B的解析式为y＝-2x﹣4，
当y＝0时，x＝-2，
∴C（-2，0）．
故选：C

【点睛】
本题考查了轴对称-最短路径问题，一次函数与坐标轴交点问题，解题关键是确定点C的位置，利用一次函数解析式求坐标．
4、C
【解析】
【分析】
利用方程组的解就是两个相应的一次函数图象的交点坐标解决问题．
【详解】
解：由表格可知，一次函数y1=k1x+b1和一次函数y2=k2x+b2的图象都经过点(2，3)，
∴一次函数y1=k1x与y=k2x+b的图象的交点坐标为(2，3)，
∴关于x，y的二元一次方程组的解为．
故选：C．
【点睛】
本题考查了一次函数图像交点坐标与方程组解的关系：对于函数y1=k1x+b1，y2=k2x+b2，其图象的交点坐标(x，y)中x，y的值是方程组的解．
5、D
【解析】
【分析】
根据图象依次分析判断．
【详解】
解：甲队的挖掘速度在2小时前小于乙队的挖掘速度，2小时后大于乙队的速度，故选项A不符合题意；
开挖2h时，乙队所挖的河渠的长度为30m，
甲队每小时挖=10m，故2h时，甲队所挖的河渠的长度为20m，
开挖2h时，甲、乙两队所挖的河渠的长度相差30-20=10m，故选项B不符合题意；
由图象可知，乙队2小时前后的挖掘速度发生了改变，故选项C不符合题意；
甲队开挖4h时，所挖河渠的长度为，
乙队开挖2小时后的函数解析式为，当开挖4h时，共挖40m，故选项D符合题意；
故选：D．
【点睛】
此题考查了一次函数的图象，利用图象得到所需信息，能读懂函数图象并结合所得信息进行计算是解题的关键．
6、B
【解析】
【分析】
根据菜园的三边的和为24m，进而得出一个x与y的关系式，然后根据题意可得关于x的不等式，求解即可确定x的取值范围．
【详解】
解：根据题意得，菜园三边长度的和为24m，
即，
所以，
由y＞0得，，
解得，
当时，即，
解得，
∴，
故选：B．
【点睛】
题目主要考查一次函数的运用及根据条件得出不等式求解，理解题意，利用不等式得出自变量的取值范围是解题关键．
7、C
【解析】
【分析】
由题意求出C和D点坐标，求出直线CD的解析式，再与直线AB解析式联立方程组即可求出交点E的坐标．
【详解】
解：令直线中，得到，故，
令直线中，得到，故，
由勾股定理可知：，
∵，且，
∴，，
过C点作CH⊥x轴于H点，过D点作DF⊥x轴于F，如下图所示：

∵为等边三角形，
∴，
∴，
∴，
∴，
∴，
同理，∵为等边三角形，
∴，，
∴，
∴，
∴，
设直线CD的解析式为：y=kx+b，代入和，
得到：，解得，
∴CD的解析式为：，
与直线联立方程组，
解得，故E点坐标为，
故选：C．
【点睛】
本题考查的是一次函数图象上点的坐标特征，本题的关键是求出点C、D的坐标，进而求解．
8、A
【解析】
【分析】
作点关于轴的对称点，连接，交轴于点，则，进而根据对称性求得当点P与重合时，的周长最小，通过求直线的解析式，即可求得点的坐标
【详解】
解：如图，作点关于轴的对称点，连接，交轴于点，则，连接，

的周长，点是定点，则的长不变，
当重合时，的周长最小，
由，令，令，则

是的中点

,点是关于轴对称的点

设直线的解析式为：，将，代入，

解得
直线的解析式为：
令，则
即
故选A
【点睛】
本题考查了轴对称的性质求最值，求一次函数解析式，求直线与坐标轴的交点，求线段中点坐标，掌握根据轴对称的性质求线段和的最值是解题的关键．
9、D
【解析】
【分析】
根据一次函数图象与系数的关系解答即可．
【详解】
解：一次函数、是常数，的图象不经过第三象限，
且，
故选：D．
【点睛】
本题主要考查了一次函数图象与系数的关系，直线y=kx+b所在的位置与k、b的符号有直接的关系为：k＞0时，直线必经过一、三象限．k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交．b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．
10、C
【解析】
【分析】
求出点A、点坐标，求出长即可求出点的坐标．
【详解】
解：当x=0时，，点B的坐标为（0，-1）；当y=0时，，解得，，点A的坐标为（2，0）；
即，，；
以点为圆心、长为半径画弧，与轴正半轴交于点，
故，则，
点C的坐标为；
故选：C
【点睛】
本题考查了一次函数与坐标轴交点坐标和勾股定理，解题关键是求出一次函数与坐标轴交点坐标，利用勾股定理求出线段长．
二、填空题
1、一次函数
【解析】
略
2、##
【解析】
【分析】
分别求得的中点的坐标，进而求得直线的交点坐标即可求得重心G的坐标．三角形的重心为三角形三条中线的交点．
【详解】
解：如图，点A点B的坐标分别是（4，8），（12，0），

,
设直线的解析式为，


解得
直线的解析式为
设直线的解析式为，


解得
直线的解析式为，
则即为的重心
即
解得

故答案为：
【点睛】
本题考查了三角形重心的定义，待定系数法求一次函数解析式，中点坐标公式，求两直线解析式，掌握三角形的重心的定义是解题的关键．
3、三
【解析】
【分析】
先根据一次函数y＝﹣2x+7判断出k、b的符号，再根据一次函数的性质进行解答即可．
【详解】
解：∵一次函数y＝﹣2x+7中，k＝﹣2＜0，b＝7＞0，
∴此函数的图象经过第一、二、四象限，
∴此函数的图象不经过第三象限．
故答案为：三．
【点睛】
本题考查了一次函数图象与系数的关系：对于y=kx+b（k为常数，k≠0），当k＞0，b＞0，y=kx+b的图象在一、二、三象限；当k＞0，b＜0，y=kx+b的图象在一、三、四象限；当k＜0，b＞0，y=kx+b的图象在一、二、四象限；当k＜0，b＜0，y=kx+b的图象在二、三、四象限．
4、 3 5
【解析】
略
5、x＜-2
【解析】
【分析】
根据图象，找出在x轴下方的函数图象所对应的自变量的取值即可得答案．
【详解】
∵点A坐标为（-2，0），
∴关于x的不等式kx+b＜0的解集是x＜-2，
故答案为：x＜-2
【点睛】
本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合；熟练掌握函数图象法是解题关键．
三、解答题
1、 (1)y甲＝25x＋2 000；y乙＝35x
(2)当0＜x＜200时，选择乙公司更优惠；当x＝200时，选择两公司费用一样多；当x＞200时，选择甲公司更优惠．理由见解析
【解析】
【分析】
（1）设甲公司制作宣传材料的费用为y甲(元)，乙公司制作宣传材料的费用为y乙(元)，份数乘以单价加上设计费可得甲公司的费用；份数乘以单价可得乙公司的费用；
（2）分三种情况讨论，当y甲＞y乙时，当y甲＝y乙时，当y甲＜y乙时，分别计算可得
(1)
解：设甲公司制作宣传材料的费用为y甲(元)，乙公司制作宣传材料的费用为y乙(元)，制作宣传材料的份数为x(份)，
依题意得y甲＝25x＋2 000；y乙＝35x；
(2)
解：当y甲＞y乙时，即25x＋2 000＞35x，
解得：x＜200；
当y甲＝y乙时，即25x＋2 000＝35x，
解得：x＝200；
当y甲＜y乙时，即25x＋2 000＜35x，
解得：x＞200.
∴当0＜x＜200时，选择乙公司更优惠；
当x＝200时，选择两公司费用一样多；
当x＞200时，选择甲公司更优惠．
【点睛】
此题考查了一元一次方程的方案选择问题，一元一次不等式类的方案选择问题，列代数式，正确理解题意是解题的关键．
2、 (1)（3，），2，3，
(2)（3，）
(3)等边三角形，见解析
(4)存在，（0，）或（0，﹣）或（2，）或（2，﹣）．
【解析】
【分析】
（1）先根据等角对等边，确定OB=OC=，再通过构造垂线法，分别求出相关线段的长，根据点所在象限，确定点的坐标；根据面积公式，选择适当的底边计算即可；利用同底的两个三角形面积之比等于对应高之比计算即可；
（2）根据点关于x轴对称的特点，直接写出坐标即可；
（3）根据三个角是60°的三角形是等边三角形判定即可；
（4）利用全等三角形的判定定理，综合运用分类思想求解．
(1)
解：（1）∵点B（0，﹣2），
∴OB＝，
∵∠COA＝∠OCA＝∠OBA＝30°，
∴OB＝OC=，
过点C作CD⊥x轴于点D，

∴CD＝=，DO==3，
∵点C在第一象限；
∴C（3，），
∴=；
∴，
故答案为：（3，），2，3，．
(2)
∵C（3，），点C与点C'关于x轴对称，
∴C'（3，﹣）．
故答案为：（3，﹣）．
(3)
∵OE⊥OC，
∴∠COE＝90°，

∵∠COA＝30°，
∴∠AOE＝60°，
∵∠OAE＝60°，
∴∠AOE＝∠OAB＝60°，
∴△OAE是等边三角形，
故答案为：等边三角形．
(4)
解：①如图1，当△AOB≌△AOF时，
∵OB＝，
∴OF＝，
∴（0，），（0，﹣），

②如图2，当△AOB≌OAF时，
设直线AB的解析式为y=kx+b，
∴，
解得，
∴直线AB的解析式为y=x，
令y=0，得x=2，
∴点A的坐标为（2，0），
∵△AOB≌OAF，
∴OB=AF=，
∴F3（2，），F4（2，﹣），

综上所述，存在点F，且点F的坐标是（0，）或（0，﹣）或（2，）或（2，﹣）．
【点睛】
本题考查了等角对等边，坐标与象限，勾股定理，点的对称，函数解析式，等边三角形的判定，三角形全等的判定，分类思想，熟练掌握待定系数法，灵活运用三角形全等的判定是解题的关键．
3、 (1)k=2；
(2)7；
(3)≤m≤3
【解析】
【分析】
（1）利用勾股定理求得B (-1，0)，再利用待定系数法即可求解；
（2）先求得直线l2的解析式，分别求得D、C、N的坐标，再利用四边形OCNB的面积=S△ODC- S△NBD求解即可；
（3）先求得点P的纵坐标，根据题意列不等式组求解即可．
(1)
解：令x=0，则y=2；
∴B (0，2)，
∴OB=2，
∵AB=；
∴OA=1，
∴A (-1，0)，
把B (-1，0)代入y=kx+2得：0=-k+2，
∴k=2；
(2)
解：∵直线l2平行于直线y=−2x．
∴设直线l2的解析式为y=−2x+b．
把(2，2)代入得2=−22+b，
解得：b=6，
∴直线l2的解析式为．
令x=0，则y=6，则D (0，6)；令y=0，则x=3，则C (3，0)，
由（1）得直线l1的解析式为．
解方程组得：，
∴N (1，4)，
四边形OCNB的面积=S△ODC- S△NBD
=
=7；
(3)
解：∵点P的横坐标为m，
∴点P的纵坐标为，
∴PM=，
∵PM≤3，且点P在线段CD上，
∴≤3，且m≤3．
解得：≤m≤3．
【点睛】
本题考查了两条直线相交与平行问题，待定系数法求函数的解析式，三角形的面积，正确的理解题意是解题的关键．
4、 (1)普通板栗的单价为55元，精品板栗的单价为80元；
(2)普通板栗加工1000件，精品板栗加工3000件，所获总利润最多，最多总利润是75000元．
【解析】
【分析】
（1）设普通板栗的单价为x元，精品板栗的单价为y元，根据表格列出二元一次方程组，求解即可得；
（2）加工普通板栗a件，则加工精品板栗(4000-a)件，根据题意可得利润的函数关系式，根据一次函数的性质及自变量的取值范围可得当时，所获总利润w最多，代入求解即可得．
(1)
解：设普通板栗的单价为x元，精品板栗的单价为y元，由题意得：
，
解得x=55y=80，
答：普通板栗的单价为55元，精品板栗的单价为80元；
(2)
解：加工普通板栗a件，则加工精品板栗(4000-a)件，
由题意得：，
∵，1000≤a≤3000，
∴当时，所获总利润w最多，
w=-5×1000+80000=75000，
∴，
答：普通板栗加工1000件，精品板栗加工3000件，所获总利润最多，最多总利润是75000元．
【点睛】
题目主要考查二元一次方程组的应用及一次函数的最大利润问题，理解题意，列出方程及函数解析式是解题关键．
5、 (1)A种产品生产400件，B种产品生产200件
(2)A种产品生产1000件时，利润最大为460000元
【解析】
【分析】
（1）设A种产品生产x件，则B种产品生产（600-x）件，根据600件产品用220000元资金，即可列方程求解；
（2）设A种产品生产x件，总利润为w元，得出利润w与A产品数量x的函数关系式，根据增减性可得，A产品生产越多，获利越大，因而x取最大值时，获利最大，据此即可求解．
(1)
解：设A种产品生产x件，则B种产品生产（600-x）件，
由题意得：，
解得：x＝400，
600-x=200，
答：A种产品生产400件，B种产品生产200件.
(2)
解：设A种产品生产x件，总利润为w元，由题意得：

由，
得：，
因为10>0，w随x的增大而增大 ，所以当x＝1000时，w最大＝460000元．
【点睛】
本题考查一元一次方程、一元一次不等式以及一次函数的实际应用. 解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．