初中数学冀教版八年级下册第二十章 函数综合与测试课后复习题

冀教版八年级数学下册第二十章函数专项测评

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、某天，小南和小开两兄弟一起从家出发到某景区旅游，开始大家一起乘坐时速为50千米的旅游大巴，出发2小时后，小南有急事需回家，于是立即下车换乘出租车，一个小时后返回家中，办事用了30分钟后自己驾车沿同一路线以返回时的速度赶往景区，结果小南比小开早30分钟到达景区（三车的速度近似匀速，上下车的时间忽略不计，两地之间为直线路程），两人离家的距离y（千米）与出发时间x（小时）的关系如图所示，则以下说法错误的是（       ）

A．出租车的速度为100千米/小时 B．小南追上小开时距离家300千米

C．小南到达景区时共用时7.5小时 D．家距离景区共400千米

2、下列各曲线中，不表示y是x的函数的是（　　）

A．  B．

C．  D．

3、在下列图象中，是的函数的是（        ）

A．  B．

C．  D．

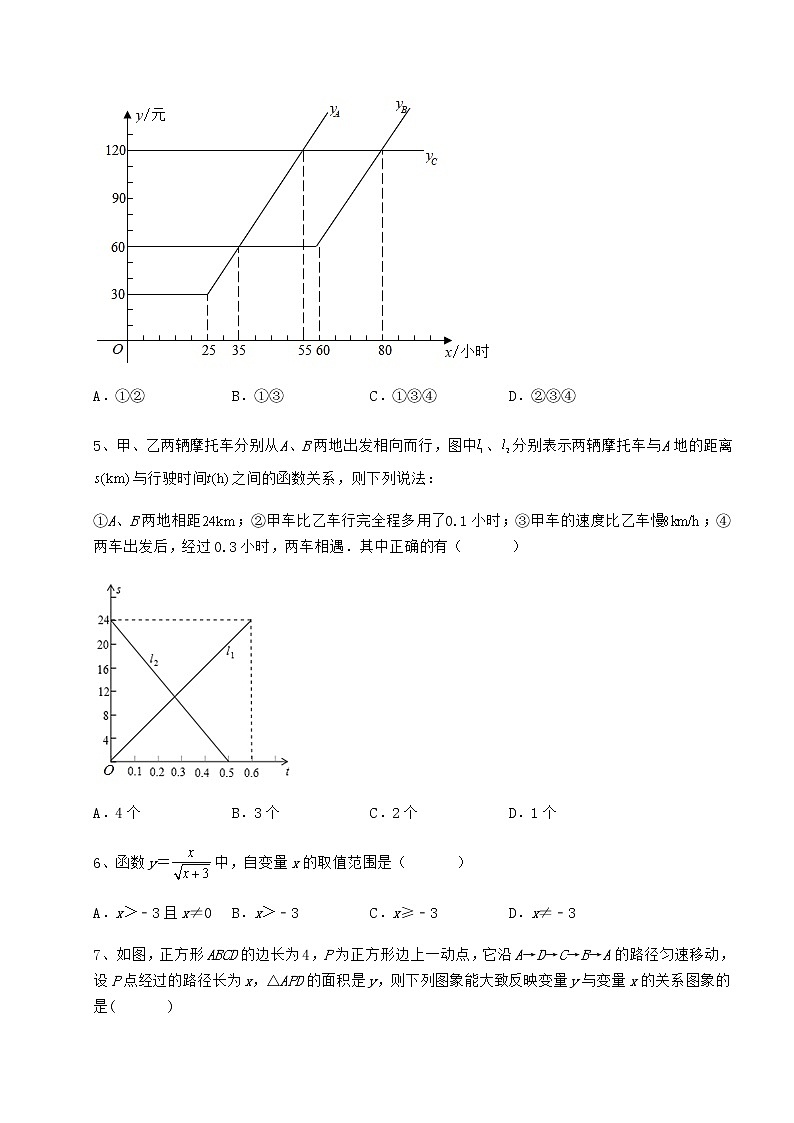
4、A，B，C三种上宽带网方式的月收费金额yA（元），yB（元），yC（元）与月上网时间x（小时）的对应关系如图所示．以下有四个推断：

①月上网时间不足35小时，选择方式A最省钱；

②月上网时间超过55小时且不足80小时，选择方式C最省钱；

③对于上网方式B，若月上网时间在60小时以内，则月收费金额为60元；

④对于上网方式A，若月上网时间超出25小时，则超出的时间每分钟收费0.05元．

所有合理推断的序号是（　　）

A．①② B．①③ C．①③④ D．②③④

5、甲、乙两辆摩托车分别从A、B两地出发相向而行，图中、分别表示两辆摩托车与A地的距离与行驶时间之间的函数关系，则下列说法：

①A、B两地相距；②甲车比乙车行完全程多用了0.1小时；③甲车的速度比乙车慢；④两车出发后，经过0.3小时，两车相遇．其中正确的有（       ）

A．4个 B．3个 C．2个 D．1个

6、函数y＝中，自变量x的取值范围是（       ）

A．x＞﹣3且x≠0 B．x＞﹣3 C．x≥﹣3 D．x≠﹣3

7、如图，正方形ABCD的边长为4，P为正方形边上一动点，它沿A→D→C→B→A的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映变量y与变量x的关系图象的是(       )

A． B．

C． D．

8、如图1所示，直角三角形中，，且．设直线截此三角形所得的阴影部分面积为，与之间的函数关系的图象为图2所示，则的周长为（       ）

A． B． C． D．

9、甲、乙两人骑车分别从A、B两地同时出发，沿同一路线匀速骑行，两人先相向而行，甲到达B地后停留20min 再以原速返回A地，当两人到达A地后停止骑行．设甲出发x min后距离A地的路程为y km．图中的折线表示甲在整个骑行过程中y与x的函数关系．在整个骑行过程中，两人只相遇了1次，乙的骑行速度（单位：km/min）可能是（   ）

A．0.1 B．0.15 C．0.2 D．0.25

10、习近平总书记在全国教育大会上强调，要坚持中国特色社会主义教育发展道路．培养德智体美劳全面发展的社会主义建设者和接班人．枣庄某学校利用周未开展课外劳动实践活动．如图反映的过程是：小强从家去菜地浇水，又去玉米地除草，然后回家．如果菜地和玉米地的距离为a千米，小强在玉米地除草比在菜地浇水多用的时间为b分钟，则a，b的值分别为（       ）

A．1.1，8 B．0.9，3 C．1.1，12 D．0.9，8

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、若球体体积为，半径为，则．其中变量是_______、_______，常量是________．

2、在中，的取值范围为______．

3、已知函数f（x）＝+x，则f（）＝_____．

4、函数y＝中，自变量x的取值范围是 ___．

5、描点法画函数图象的一般步骤：

第一步：______．在自变量取值范围内选定一些值．通过函数关系式求出对应函数值列成表格．

第二步：______．在直角坐标系中，以自变量的值为横坐标，相应函数值为纵坐标，描出表中对应各点．

第三步：______．按照坐标由小到大的顺序把所有点用平滑曲线连结起来．

三、解答题（5小题，每小题10分，共计50分）

1、A，B两地相距60km，甲乙两人沿同一条路从A地前往B地，甲先出发．图中l1，l2表示甲乙两人离A地的距离y（km）与乙所用时间x（h）之间的关系，请结合图象回答下列问题：

（1）图中表示甲离A地的距离y（km）与乙所用时间x（h）之间关系的是 　 　（填l1或l2）；

（2）当其中一人到达B地时，另一人距B地 　 　km；

（3）乙出发多长时间时，甲乙两人刚好相距10km？

2、小华骑电动车从家出发去西安交大，当他骑了一段路时，想起要买一本书，于是原路返回刚经过的新华书店，买到书后继续前往交大，如图是他离家的距离与时间的关系示意图，请根据图中提供的信息回答下列问题：

（1）小华家离西安交大的距离是多少？

（2）买到书后，小华从新华书店到西安交大骑车的平均速度是多少？

（3）本次去西安交大途中，小华一共行驶了多少米？

3、分别对各函教解析式进行讨论：

；        ；       

（1）自变量x在什么范围内取值时函数解析式有意义？

（2）当时对应的函数值是多少？

4、一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），如图中的折线表示）与x之间的函数关系．根据图象进行以下探究：

[信息读取]

（1）甲，乙两地相距______千米，两车出发后______小时相遇；

（2）普通列车到达终点共需______小时，普通列车的速度是______千米/小时：

[解决问题]

（3）求动车的速度：

（4）求点C的坐标．

5、甲、乙两车从城出发沿一条笔直公路匀速行驶至城，在整个行驶过程中，甲、乙两车离开城的距离与甲车行驶的时间之间的函数关系如图所示．

(1)、两城相距_____千米，乙车比甲车早到______小时；

(2)求出点坐标；

(3)两车都在行驶的过程中，当甲、乙两车相距40千米时，_____．

-参考答案-

一、单选题

1、B

【解析】

【分析】

先根据旅游大巴2小时行2×50=100千米，出租车1小时行驶100千米，出租车速度可判断A正确；设小南t小时追上小开，利用两者距离相等列方程 50（2+1+0.5+t）=100t，解得t=3.5，可判断B不正确；利用到旅游区两者距离相等列方程50（2+1+0.5+t+0.5）=100t，解得t=4，可判断C正确；利用自驾车行驶速度×时间=100×4=400千米，可求出家距离景区共400千米，可判断D正确．

【详解】

解：旅游大巴2小时行2×50=100千米，出租车1小时行驶100千米，出租车速度为100÷1=100千米/时，

故选项A正确；

设小南t小时追上小开，

50（2+1+0.5+t）=100t，

解得t=3.5，

∴100×3.5=350千米，

故选项B不正确；

50（2+1+0.5+t+0.5）=100t，

解得t=4，

∴小南到达景区时共用2+1+0.5+4=7.5小时，

故选项C正确；

∵100×4=400千米，

∴家距离景区共400千米，

故选项D正确．

故选B．

【点睛】

本题考查函数图像信息获取与处理，掌握函数图像信息获取与处理方法是解题关键．

2、D

【解析】

【分析】

根据函数的意义进行判断即可．

【详解】

解：A、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；

B、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；

C、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；

D、图中，对于的每一个取值，可能有两个值与之对应，选项符合题意．

故选：D．

【点睛】

本题主要考查了函数的定义，解题的关键是掌握函数的定义，在定义中特别要注意，对于的每一个值，都有唯一的值与其对应．

3、D

【解析】

【分析】

设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量．根据函数的意义即可求出答案．

【详解】

解：A、对于x的每一个确定的值，y可能会有两个值与其对应，不符合函数的定义，故选项A不符合题意；

B、对于x的每一个确定的值，y可能会有多个值与其对应，不符合函数的定义，故选项B不符合题意；

C、对于x的每一个确定的值，y可能会有两个值与其对应，不符合函数的定义，故选项C不符合题意；

D、对于x的每一个确定的值，y有唯一的值与之对应，符合函数的定义，故选项D符合题意．

故选：D．

【点睛】

本题主要考查了函数的定义．解题的关键是掌握函数的定义，在定义中特别要注意，对于x的每一个值，y都有唯一的值与其对应．

4、C

【解析】

【分析】

根据A，B，C三种上宽带网方式的月收费金额yA（元），yB（元），yC（元）与月上网时间x（小时）的图象逐一判断即可．

【详解】

由图象可知：

①月上网时间不足35小时，选择方式A最省钱，说法正确；

②月上网时间超过55小时且不足80小时，选择方式B最省钱，故原说法错误；

③对于上网方式B，若月上网时间在60小时以内，则月收费金额为60元，说法正确；

④对于上网方式A，若月上网时间超出25小时，则超出的时间每分钟收费为：（60﹣30）÷[（35﹣25）×60]＝0.05（元），原说法正确；

所以所有合理推断的序号是①③④．

故选：C．

【点睛】

本题考查了函数的图象，掌握数形结合的方法是解答本题的关键．

5、B

【解析】

【分析】

根据从B到A共行驶的路程可判断①；求出乙车行驶时间，甲车行驶时间，根据减法求出时间差可判断②；根据时间与路程，求出甲乙两车的速度，根据减法求出速度差可判断③；设两相遇时间为th.甲车行驶40tkm,乙车行驶48tkm，根据甲乙共走全程列方程，求出时间t可判断④．

【详解】

解：乙从B地到A共行走24km，故①A、B两地相距正确；

乙摩托车从B到A地用0.5h，甲摩托车从A地到B地用0.6h，

∴0.6-0.5=0.1h，故②甲车比乙车行完全程多用了0.1小时正确；

甲摩托车行驶的速度为24÷0.6=40km/h，乙摩托车行驶的速度为24÷0.4=48km/h，

∴48-40=8km/h，

故③甲车的速度比乙车慢正确；

设两车相遇时间为th.甲车行驶40tkm,乙车行驶48tkm，

∴40t+48t=24，

解得h，

故④两车出发后，经过0.3小时，两车相遇不正确．

故选择B．

【点睛】

本题考查从行程图像获取信息和处理信息，看懂函数图像，列一元一次方程，时间差，速度差，掌握相关知识是解题关键．

6、B

【解析】

【分析】

根据二次根式和分式有意义的条件：被开方数大于等于0，分母不为0列式计算即可．

【详解】

解：∵函数y＝，

∴，解得：x＞﹣3．

故选：B．

【点睛】

本题考查函数基本知识，解题的关键是掌握二次根式和分式有意义的条件．

7、B

【解析】

【分析】

根据动点P的正方形各边上的运动状态分类讨论△APD的面积即可；

【详解】

由点P运动状态可知，当0≤x≤4时，点P在AD上运动，△APD的面积为0；

当4≤x≤8时，点P在DC上运动，△APD的面积y＝×4×（x﹣4）＝2x﹣8；

当8≤x≤12时，点P在CB上运动，△APD的面积y＝8；

当12≤x≤16时，点P在BA上运动，△APD的面积y＝×4×（16﹣x）＝﹣2x+32；

故选B．

【点睛】

本题主要考查了正方形的性质，动点问题与函数图象结合，准确分析计算是解题的关键．

8、D

【解析】

【分析】

由函数图象可得：阴影部分的最大面积为：3， 再利用面积公式求解 再利用勾股定理求解 从而可得答案.

【详解】

解：由函数图象可得：阴影部分的最大面积为：3，

，且，

解得： （负根舍去）

所以的周长为：

故选D

【点睛】

本题考查的是从函数图象中获取信息，等腰直角三角形的性质，勾股定理的应用，二次根式的化简与加减运算，灵活应用以上知识解题是关键.

9、D

【解析】

【分析】

由函数图象可求出甲、乙骑行的时间，根据题意和路程÷时间=速度可求出乙的最小速度即可求解．

【详解】

解：由函数图象知，A、B两地的距离为25km，甲往返的时间为50+50+20=120（min），

∵两人到达A地后停止骑行，且在整个骑行过程中，两人只相遇了1次，

∴乙的骑行的速度至少为25÷120= （km/min），

∵＞0.2，＜0.25，

∴乙的骑行速度可能是0.25km/min，

故选：D．

【点睛】

本题考查一次函数的应用，理解题意，准确从图象中获取有效信息是解答的关键．

10、D

【解析】

【分析】

直接根据函数图像进行解答即可．

【详解】

解：此函数大致可分以下几个阶段：

①0﹣15分种，小强从家走到菜地；

②15﹣25分钟，小强在菜地浇水；

③25﹣37分钟，小强从菜地走到玉米地；

④37﹣55分钟，小强在玉米地除草；

⑤55﹣80分钟，小强从玉米地回到家；

综合上面的分析得：由③的过程知，a＝2﹣1.1＝0.9千米；

由②、④的过程知b＝（55﹣37）﹣（25﹣15）＝8分钟；

故选：D．

【点睛】

本题考查了从函数图像中提取信息，读懂题意，理解函数图像的含义是解本题的关键．

二、填空题

1、              

【解析】

【分析】

根据函数常量与变量的知识点作答．

【详解】

∵函数关系式为，

∴是自变量，是因变量，是常量．

故答案为：，，．

【点睛】

本题考查了常量与变量的知识，解题关键是熟记变量是指在程序的运行过程中随时可以发生变化的量．

2、x>-3

【解析】

【分析】

根据二次根式的被开方数是非负数、分母不为0列出不等式，解不等式得到答案．

【详解】

解：由题意得：2x+6>0，

解得：x>-3，

故答案为：x>-3．

【点睛】

本题考查的是二次根式有意义的条件，掌握二次根式的被开方数是非负数、分母不为0是解题的关键．

3、

【解析】

【分析】

根据题意直接把x＝代入解析式进行计算即可求得答案．

【详解】

解：∵函数f（x）＝+x，

∴f（）＝+＝2，

故答案为：2．

【点睛】

本题考查函数图象上点的坐标特征以及二次根式运算，注意掌握图象上点的坐标适合解析式．

4、x≠1．

【解析】

【分析】

根据分母不能为0，可得x−1≠0，即可解答．

【详解】

解：根据题意得：x−1≠0，

解得：x≠1．

故答案是：x≠1．

【点睛】

本题考查了函数自变量的取值范围，解决本题的关键是明确分母不能为0．

5、     列表     描点     连线

【解析】

略

三、解答题

1、（1）；（2）10；（3）乙出发1小时或3小时时，甲乙两人刚好相距10km

【解析】

【分析】

（1）根据甲比乙先出发，则当乙出发时，甲离A地已经有一段的距离，即在函数图像上表现为当时，，由此求解即可；

（2）先求出甲的速度为10千米/小时，乙的速度为20千米/小时，即可求出乙到达B地需要的时间=60÷20=3小时，则此时甲所走的距离=20+10×3=50千米，由此即可得到答案；

（3）分乙追上甲前和乙追上甲后两种情况讨论求解即可．

【详解】

解：（1）∵甲比乙先出发，

∴当乙出发时，甲离A地已经有一段的距离，即在函数图像上表现为当时，，

∴表示甲离A地的距离y（km）与乙所用时间x（h）之间关系的是，

故答案为：；

（2）由函数图像可知，乙两小时行驶了40千米，甲2小时行驶了20千米，

∴甲的速度为10千米/小时，乙的速度为20千米/小时，

∴乙到底B地需要的时间=60÷20=3小时，

∴此时甲所走的距离=20+10×3=50千米，

∴此时甲距离B地的距离=60-50=10千米，

故答案为：10；

（3）设乙出发t小时时，甲乙两人刚好相距10km，

当乙未追上甲时：，

解得，

当乙追上甲后：，

解得，

∴乙出发1小时或3小时时，甲乙两人刚好相距10km．

【点睛】

本题主要考查了从函数图像获取信息，解题的关键在于能够准确读懂函数图像．

2、（1）4800米；（2）450米/分；（3）6800米

【解析】

【分析】

（1）根据函数图象，直接可得小华家到西安交大的路程；

（2）根据函数图象求得从新华书店到西安交大的路程和时间，根据速度等于路程除以时间即可求得；

（3）根据函数图象可得路程为3段，将其相加即可．

【详解】

解：（1）根据函数图象，可知小华家到西安交大的路程是4800米；

（2）小华从新华书店到西安交大的路程为4800﹣3000＝1800米，所用时间为28﹣24＝4分钟，

小华从新华书店到西安交大骑车的平均速度是1800÷4=450米/分；

（3）根据函数图象，小华一共行驶了4800＋2×（4000﹣3000）＝6800（米）．

【点睛】

本题考查了函数图象，要理解横纵坐标表示的含义以及小华的运动过程，从函数图象中获取信息是解题的关键．

3、（1），x可为任意实数；；．（2）；；．

【解析】

【分析】

（1）根据整式有意义的条件：全体实数，分式有意义的条件：分母不为0，二次根式有意义的条件：被开方数大于等于0即可求解；

（2）将分别代入各式计算即可．

【详解】

解：（1）∵整式有意义的条件是全体实数，

∴有意义时自变量x取值范围是全体实数，

∵分式有意义的条件是分母不为0，

∴有意义时自变量x取值范围，即，

∵二次根式有意义的条件：被开方数大于等于0，

∴有意义时自变量x取值范围，即；

（2）将代入，得：，

将代入，得：，

将代入，得：．

【点睛】

本题考查函数自变量取值范围及函数值的定义，解题的关键是熟练掌握各式有意义的条件．

4、（1）1800；4；（2）12；150；（3）300km/h；（4）

【解析】

【分析】

（1）初始时刻y=1800，即为两地距离，相遇时两车距离为0，由图像得到相遇时刻；

（2）最后到达的为普通列车，根据路程除以时间可得速度；

（3）根据动车4小时到达，利用速度=路程÷时间求解即可；

（4）由函数图像可知m时刻是动车到达乙地的时刻，用路程除以速度即可．

【详解】

（1）由图像可知，甲地与乙地相距1800千米，两车出发后4小时相遇；

故答案为：1800，4；

（2）由函数图像可知，普通列车12小时到达，则速度为1800÷12=150千米/小时

故答案为：12；150；.

（3）由题意得：动车的速度为： （km/h）；

（4），

∴，，

∴点的坐标为．

【点睛】

本题主要考查了从函数图像获取信息，解题的关键在于能够准确读懂函数图像．

5、 (1)300千米，1小时

(2)

(3)或

【解析】

【分析】

（1）根据图象，即可求解；

（2）根据图象，可得乙车在点追上甲车，再求出两车的速度，然后设甲车出发小时后，乙车追上甲车，可得，解出即可求解；

（3）分两种情况讨论，即可求解．

(1)

解：由图象可得，

，两城相距300千米，乙车比甲车早到（小时）；

(2)

解：由图象可得，乙车在点追上甲车，

甲车的速度为（千米/时），乙车的速度为（千米/时），

设甲车出发小时后，乙车追上甲车，

，

解得，

∴（千米），

∴点；

(3)

解：根据题意得：当乙车没有追上甲车前，甲、乙两车相距40千米时，

，

解得： ；

当乙车超过甲车后，甲、乙两车相距40千米时，

，

解得：；

综上所述，当甲、乙两车相距40千米时，或．

【点睛】

本题主要考查了函数图象，从函数图象获取准确信息，并利用数形结合思想解答是解题的关键．