初中数学第九章 三角形综合与测试课堂检测

这是一份初中数学第九章 三角形综合与测试课堂检测，共23页。试卷主要包含了若三角形的两边a，如图，直线l1l2，被直线l3等内容，欢迎下载使用。
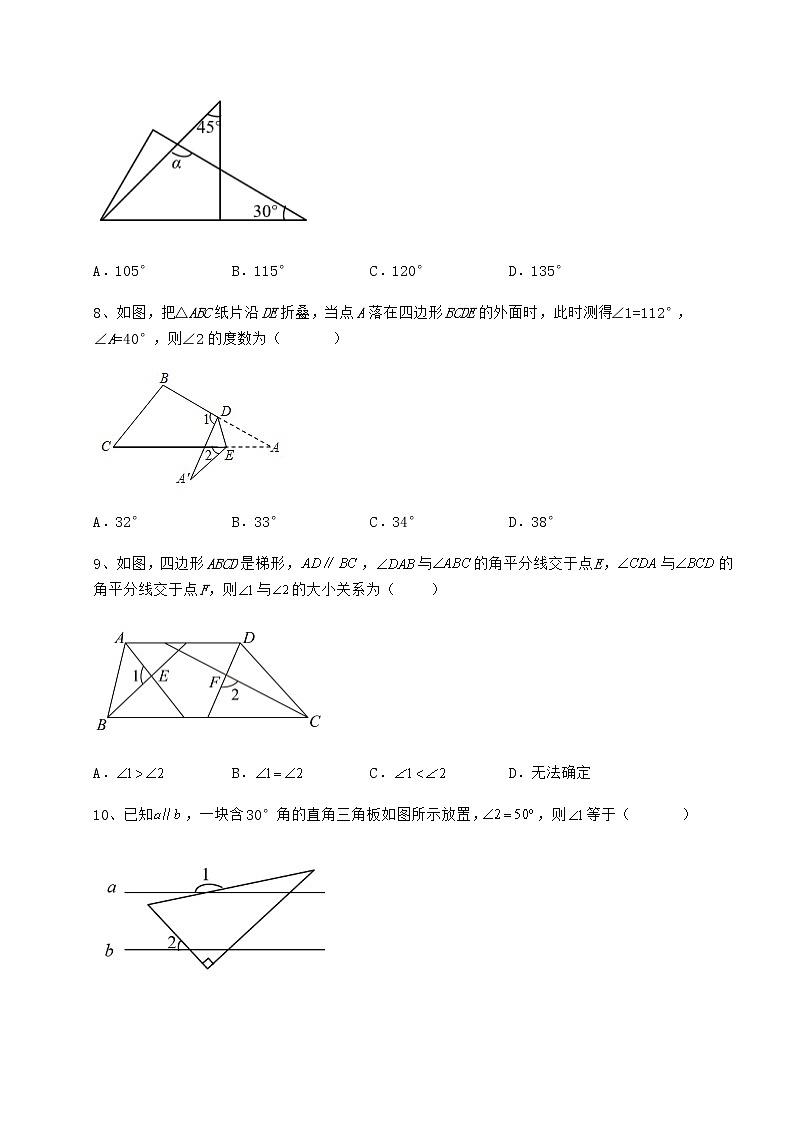
冀教版七年级数学下册第九章 三角形同步测评 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、若一个三角形的两条边的长为5和7，那么第三边的长可能是（       ）A．2 B．10 C．12 D．132、将一副直角三角板按如图所示的位置摆放，若含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则的度数是（       ）A．45° B．60° C．75° D．85°3、如图，在中，若点使得，则是的（       ）A．高 B．中线 C．角平分线 D．中垂线4、若三角形的两边a、b的长分别为3和4，则其第三边c的取值范围是（     ）A．3＜c＜4 B．2≤c≤6 C．1＜c＜7 D．1≤c≤75、如图，在中，D是延长线上一点，，，则的度数为（       ）A． B． C． D．6、如图，直线l1l2，被直线l3、l4所截，并且l3⊥l4，∠1＝46°，则∠2等于（　　）A．56° B．34° C．44° D．46°7、如图所示，一副三角板叠放在一起，则图中等于（       ） A．105° B．115° C．120° D．135°8、如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外面时，此时测得∠1=112°，∠A=40°，则∠2的度数为（       ）A．32° B．33° C．34° D．38°9、如图，四边形ABCD是梯形，，与的角平分线交于点E，与的角平分线交于点F，则与的大小关系为（     ）A． B． C． D．无法确定10、已知，一块含30°角的直角三角板如图所示放置，，则等于（       ）A．140° B．150° C．160° D．170°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在△ABC中，点D在CB的延长线上，∠A＝60°，∠ABD＝110°，则∠C等于___．2、如图，，，BE平分交AD于点E，连接CE，AF交CD的延长线于点F，，若，，则的度数为______．3、如图，一副三角板按如图放置，则∠DOC的度数为______．4、如图，∠ABD＝80°，∠C＝38°，则∠D＝___度．5、如图，将一张三角形纸片ABC的一角折叠，使得点A落在四边形BCDE的外部A'的位置，且A'与点C在直线AB的异侧，折痕为DE，已知∠C＝90°，∠A＝30°．若保持△A′DE的一边与 BC平行，则∠ADE的度数______．三、解答题（5小题，每小题10分，共计50分）1、如图，BD是的角平分线，BE是的AC边上的中线．（1）若的周长为13，，，求AB的长．（2）若，，求的度数．2、在△ABC中，∠A－∠B＝30°，∠C＝4∠B，求∠A、∠B、∠C的度数3、已知：如图，在△ABC中，AB＝3，AC＝5．（1）直接写出BC的取值范围是　   　．（2）若点D是BC边上的一点，∠BAC＝85°，∠ADC＝140°，∠BAD＝∠B，求∠C．4、（1）先化简，再求值：，其中a＝4．（2）若a，b，c分别为三角形的三边，化简：|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|5、如图，在三角形ABC中，∠ABC与∠ACB的角平分线交于点P(1)当∠A=60°时，求∠BPC的的度数；（提示：三角形内角和180°）；(2)当∠A=α°时，直接写出∠A与∠BPC的数量关系． -参考答案-一、单选题1、B【解析】【分析】根据在三角形中三边关系可求第三边长的范围，再选出答案．【详解】解：设第三边长为x，则由三角形三边关系定理得7-5＜x＜7+5，即2＜x＜12．只有选项B符合题意，故选：B．【点睛】本题考查了三角形三边关系，掌握三角形的三边关系是解题的关键．三角形的三边关系：三角形两边之和大于第三边，两边之差小于第三边．2、C【解析】【分析】先根据三角形的内角和得出∠CGF=∠DGB=45°，再利用∠α=∠D+∠DGB可得答案．【详解】解：如图:∵∠ACD=90°、∠F=45°，∴∠CGF=∠DGB=45°，∴∠α=∠D+∠DGB=30°+45°=75°．故选C．【点睛】本题主要考查三角形的外角的性质，掌握三角形的内角和定理和三角形外角的性质是解答本题的关键．3、B【解析】【分析】根据三角形的中线定义即可作答．【详解】解：∵BD=DC，∴AD是△ABC的中线，故选：B．【点睛】本题考查了三角形的中线概念，三角形一边的中点与此边所对顶点的连线叫做三角形的中线．4、C【解析】【分析】根据三角形的两边之和大于第三边，两边之差小于第三边，即可求解．【详解】解：∵三角形的两边a、b的长分别为3和4，∴其第三边c的取值范围是 ，即 ．故选：C【点睛】本题主要考查了三角形的三边关系，熟练掌握三角形的两边之和大于第三边，两边之差小于第三边是解题的关键．5、B【解析】【分析】根据三角形外角的性质可直接进行求解．【详解】解：∵，，∴；故选B．【点睛】本题主要考查三角形外角的性质，熟练掌握三角形外角的性质是解题的关键．6、C【解析】【分析】依据l1∥l2，即可得到∠3＝∠1＝46°，再根据l3⊥l4，可得∠2＝90°﹣46°＝44°．【详解】解：如图：∵l1∥l2，∠1＝46°，∴∠3＝∠1＝46°，又∵l3⊥l4，∴∠2＝90°﹣46°＝44°，故选：C．【点睛】本题考查了平行线性质以及三角形内角和，平行线的性质：两直线平行，同位角相等以及三角形内角和是180°．7、A【解析】【分析】根据直角三角板各角的度数和三角形外角性质求解即可．【详解】解：如图，∠C=90°，∠DAE=45°，∠BAC=60°，∴∠CAO=∠BAC－∠DAE=60°－45°=15°，∴=∠C+∠CAO=90°+15°=105°，故选：A．【点睛】本题考查三角板中的度数计算、三角形的外角性质，熟知三角板各角度数，掌握三角形的外角性质是解答的关键．8、A【解析】【分析】由折叠的性质可知，再由三角形外角的性质即可求出的大小，再次利用三角形外角的性质即可求出的大小．【详解】如图，设线段和线段交于点F．由折叠的性质可知．∵，即，∴．∵，即，∴．故选A．【点睛】本题考查折叠的性质，三角形外角的性质．利用数形结合的思想是解答本题的关键．9、B【解析】【分析】由AD∥BC可得∠BAD+∠ABC=180°，∠ADC+∠BCD=180°，由角平分线的性质可得∠AEB=90°，∠DFC=90°，由三角形内角和定理可得到∠1=∠2=90°．【详解】解：∵AD∥BC，∴∠BAD+∠ABC=180°，∠ADC+∠BCD=180°，∵∠DAB与∠ABC的角平分线交于点E，∠CDA与∠BCD的角平分线交于点F，∴∠BAE=∠BAD，∠ABE=∠ABC，∠CDF=∠ADC，∠DCF=∠BCD，∴∠BAE+∠ABE=(∠BAD+∠ABC)=90°，∠CDF+∠DCF=(∠ADC+∠BCD) =90°，∴∠1=180°-(∠BAE+∠ABE)= 90°，∠2=∠CDF+∠DCF= 90°，∴∠1=∠2=90°，故选：B．【点睛】本题考查了平行线的性质，角平分线的定义，三角形内角和定理，灵活运用这些性质进行推理是本题的关键．10、D【解析】【分析】利用三角形外角与内角的关系，先求出∠3，利用平行线的性质得到∠4的度数，再利用三角形外角与内角的关系求出∠1．【详解】解：∵∠C＝90°，∠2＝∠CDE＝50°，∠3＝∠C+∠CDE＝90°+50°＝140°．∵a∥b，∴∠4＝∠3＝140°．∵∠A＝30°∴∠1＝∠4+∠A＝140°+30°＝170°．故选：D．【点睛】本题考查了平行线的性质，三角形的外角的性质，熟练掌握平行线的性质是解题的关键．二、填空题1、50°【解析】【分析】首先根据平角的概念求出的度数，然后根据三角形内角和定理即可求出的度数．【详解】解：∵∠ABD＝110°，∴，∴故答案为：50°．【点睛】此题考查了平角的概念，三角形三角形内角和定理，解题的关键是熟练掌握平角的概念，三角形三角形内角和定理．2、80°##80度【解析】【分析】先根据，，得出，可证AD∥BC，再证∠BAD=∠BCD，得出∠AEB=∠F，然后证∠ABC=2∠CBE=2∠F，得出∠ADC=2∠F，利用三角形内角和得出∠CED=180°-∠EDC-∠ECD=180°-2∠F-3∠F=180°-5∠F，根据平角得出∠AEB+∠CED=180°-∠BEC=180°-80°=100°，列方程∠F+180°-5∠F=100°求出∠F=20°即可．【详解】解：∵，∴∠ABC+∠BCD=180°，∵∴，∴AD∥BC，∵，∴∠BAD+∠ADC=180°，∠BAF+∠F=180°，∵∠ADC+∠BCD=180°，∴∠BAD=∠BCD，∵，∴，∵∠BAF=∠BAD+∠DAF，∴∠BAF+∠AEB=180°，∴∠AEB=∠F，∵AD∥BC，∴∠CBE=∠AEB，∵BE平分，∴∠ABC=2∠CBE=2∠F，∴∠ADC=2∠F，∵，在△CED中，∠CED=180°-∠EDC-∠ECD=180°-2∠F-3∠F=180°-5∠F，∵，∴∠AEB+∠CED=180°-∠BEC=180°-80°=100°，∴∠F+180°-5∠F=100°，解得∠F=20°，∴，故答案为80°．【点睛】本题考查平行线的判定与性质，三角形内角和，角平分线定义，平角，解一元一次方程，掌握平行线的判定与性质，三角形内角和，角平分线定义，平角，解一元一次方程，关键是证出∠ADC=2∠F．3、【解析】【分析】根据题意得：∠ACB=30°，∠ACD=45°，∠D=90°，从而得到∠OCD=15°，再由再由直角三角形两锐角互余，即可求解．【详解】解：根据题意得：∠ACB=30°，∠ACD=45°，∠D=90°，∴∠OCD=∠ACD-∠ACB=15°，∴∠DOC=90°-∠OCD=75°．故答案为：75°【点睛】本题主要考查了直角三角形的性质，根据题意得到∠ACB=30°，∠ACD=45°，∠D=90°是解题的关键．4、5、45°或30°【解析】【分析】分DA'BC或EA'BC两种情况，分别画出图形，即可解决问题．【详解】解：当DA'BC时，如图，∠A'DA=∠ACB=90°，∵△ADE沿DE折叠到A'DE，∴∠ADE=∠A'DE=∠ADA′＝45°，当EA'BC时，如图，在△ABC中，∠B=180°-∠C-∠A=60°，∴∠2=∠ABC=60°，由折叠可知，∠A′=∠A=30°，在△A′EF中，∠A′+∠2+∠A′FE=180°，∴∠2=180°-∠A′-∠A′FE=150°-∠A′FE，在四边形BCDF中，∠1+∠C+∠B+∠BFD=360°，∴∠1=360°-∠C-∠B-∠BFD=210°-∠BFD，∵∠BFD=∠A′FE，∴∠1-∠2=210°-150°=60°，∴∠1=∠2+60°=120°，∵△ADE沿DE折叠到A'DE，∴∠ADE=∠A'DE=∠ADA′=（180°-∠1）=30°，综上所述，∠ADE的度数为：45°或30°．故答案为：45°或30°．【点睛】本题主要考查了翻折的性质，平行线的性质等知识，能根据题意，运用分类讨论思想分别画出图形是解题的关键．三、解答题1、（1）3；（2）．【解析】【分析】（1）首先根据中线的性质得到，然后根据的周长为13，即可求出AB的长；（2）首先根据BD是的角平分线得到，然后根据三角形内角和定理即可求出的度数．【详解】（1）∵BE是的AC边上的中线，∴，又∵的周长为13，∴；（2）∵BD是的角平分线，∴，又∵，∴．【点睛】此题考查三角形中线和角平分线的概念，三角形内角和定理的运用，解题的关键是熟练掌握三角形中线和角平分线的概念，三角形内角和定理．2、，，【解析】【分析】根据三角形内角和定理，以及已知条件列三元一次方程组解方程求解即可【详解】在△ABC中，,∠A－∠B＝30°，∠C＝4∠B，①-②得④将③代入④解得,，，【点睛】本题考查了三角形内角和定理，解三元一次方程组，正确的计算是解题的关键．3、（1）2＜BC＜8；（2）25°【解析】【分析】（1）根据三角形三边关系解答即可；（2）根据三角形外角性质和三角形内角和解答即可．【详解】解：（1）∵AC-AB＜BC＜AC+AB，AB＝3，AC＝5．∴2＜BC＜8，故答案为：2＜BC＜8（2）∵∠ADC是△ABD的外角∴∠ADC＝∠B+∠BAD＝140∵∠B＝∠BAD∴∠B＝∵∠B+∠BAC+∠C＝180∴∠C＝180﹣∠B﹣∠BAC即∠C＝180﹣70﹣85＝25【点睛】本题考查了三角形第三边的取值范围，三角形内角和定理和三角形外角的性质，能根据三角形的外角的性质求出∠B的度数是解此题的关键．4、（1）a－1；3；（2）－a＋b＋3c．【解析】【分析】（1）先根据单项式乘以多项式法则及平方差公式展开，合并得出最简结果，再代入求值即可得答案；（2）根据三角形的三边关系可得绝对值内的式子的符号，根据绝对值的性质化简即可得答案．【详解】（1）a（1－4a）＋（2a＋1）（2a－1）＝a－4a2＋4a2－1＝a－1，当a＝4时，原式＝4－1＝3．（2）∵a、b、c为三角形三边的长，∴a＋b＞c，a＋c＞b，b＋c＞a，∴|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|＝|a－（b＋c）|＋|b－（c＋a）|＋|（c＋b）－a|＝b＋c－a＋a＋c－b＋c＋b－a＝－a＋b＋3c．【点睛】本题考查单项式乘以多项式法则、平方差公式、三角形三边关系及绝对值的性质，三角形任意两边的和大于第三边；任意两边的差小于第三边；熟练掌握相关运算法则及性质是解题关键．5、 (1)120°(2)∠BPC=【解析】【分析】（1）根据BP是∠ABC的平分线，得出∠PBC=．根据CP是∠ACB的平分线，∠PCB=，根据∠A=60°，得出=120°，求∠PBC+∠PCB==60°即可；（2）根据BP是∠ABC的平分线，得出∠PBC=．根据CP是∠ACB的平分线，得出∠PCB=，根据∠A=α°，得出=180°-α°，可求∠PBC+∠PCB=即可．(1)解：如图，∵BP是∠ABC的平分线，∴∠PBC=．(角平分线定义)∵CP是∠ACB的平分线，∴∠PCB=，∴∠PBC+∠PCB= ，∵∠A=60°，∴=120°，∴∠PBC+∠PCB==60°，∴∠BPC=180°－∠PBC－∠PCB=180°－（∠PBC+∠PCB）=180°-60°=120°．(2)如图，∵BP是∠ABC的平分线，∴∠PBC=．(角平分线定义)∵CP是∠ACB的平分线，∴∠PCB=，∴∠PBC+∠PCB=，∵∠A=α°，∴=180°-α°，∴∠PBC+∠PCB=，∴∠BPC=180°－∠PBC－∠PCB=180°－（∠PBC+∠PCB）=180°-90°=90°．∴∠BPC=．【点睛】本题考查角平分线定义，三角形内角和，掌握角平分线定义，三角形内角和是解题关键．