冀教版七年级下册第八章 整式乘法综合与测试课后练习题

冀教版七年级数学下册第八章整式的乘法必考点解析

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  0分）

一、单选题（10小题，每小题0分，共计0分）

1、已知am=5，an=2，则a2m+n的值等于（       ）

A．50 B．27 C．12 D．25

2、数字2500000用科学记数法为（       ）

A．0.25×107 B．2.5×107 C．2.5×106 D．25×105

3、已知，，则下列关系成立的是（       ）

A．m＋1＝5n B．n＝2m C．m＋1＝n D．2m＝5＋n

4、下列计算正确的是（       ）

A． B． C． D．

5、下列计算正确的是   (    )

A． B．

C． D．

6、若的结果中不含项，则的值为（       ）

A．0 B．2 C． D．-2

7、2021年12月6日，根据国家统计局发布的数据，我国粮食总产量再度实现增长，实现了“十八连丰”，达到13657亿斤．将13657亿用科学记数法表示为（       ）

A． B． C． D．

8、如果多项式 x2  mx  4 恰好是某个整式的平方，那么 m 的值为（       ）

A．2 B．－2 C．±2 D．±4

9、在幼发拉底河岸的古代庙宇图书馆遗址里，曾经发掘出大量的黏土板，美索不达米亚人在这些黏土板上刻出来乘法表、加法表和平方表．用这些简单的平方表，美索不达米亚人这样计算：第一步：（103+95）÷2＝99，第二步（103﹣95）÷2＝4；第三步：查平方表；知99的平方是9801，第四步：查平方表，知4的平方是16，第五步： 设两因数分别为a和b，写出蕴含其中道理的整式运算（　　）

A．

B．

C．

D．

10、已知，，c＝（0.8）﹣1，则a，b，c的大小关系是（       ）

A．c＞b＞a B．a＞c＞b C．a＞b＞c D．c＞a＞b

第Ⅱ卷（非选择题  100分）

二、填空题（5小题，每小题4分，共计20分）

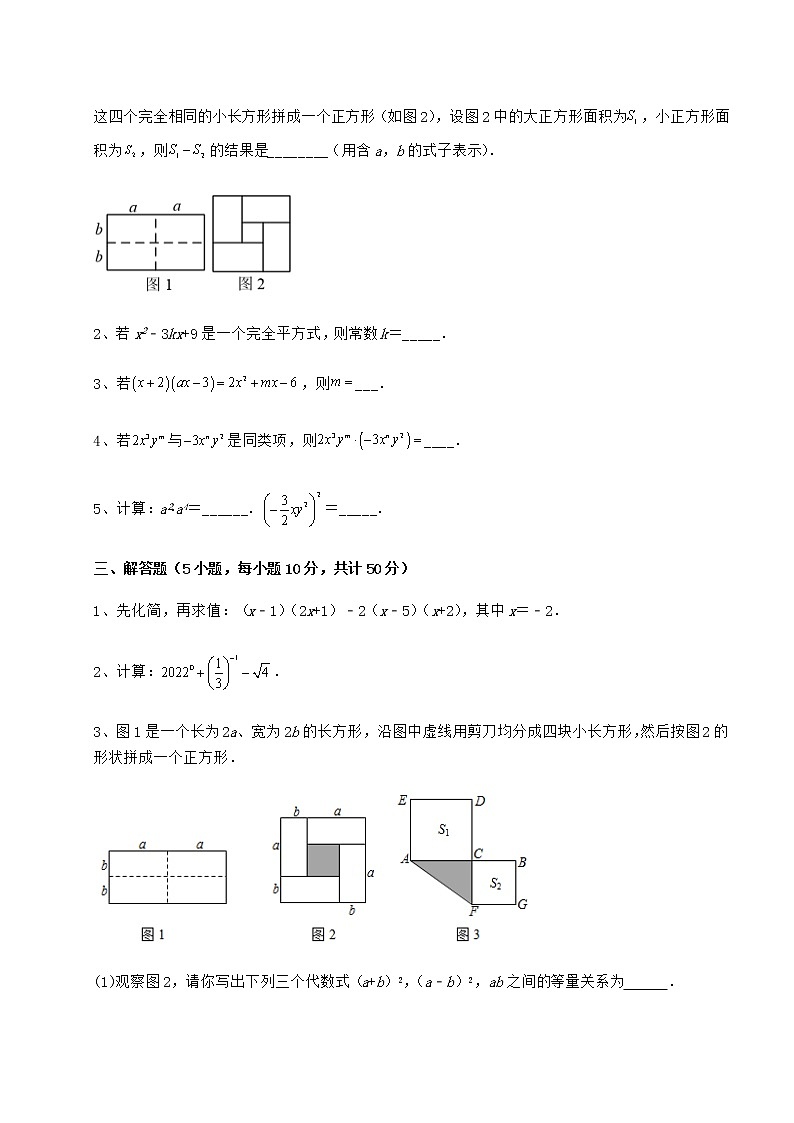
1、如图1，将一个长为2a，宽为2b的长方形沿图中虚线剪开分成四个完全相同的小长方形，然后将这四个完全相同的小长方形拼成一个正方形（如图2），设图2中的大正方形面积为，小正方形面积为，则的结果是________（用含a，b的式子表示）．

2、若x2﹣3kx+9是一个完全平方式，则常数k＝_____．

3、若，则___．

4、若与是同类项，则____．

5、计算：a2⋅a4＝______．＝_____．

三、解答题（5小题，每小题10分，共计50分）

1、先化简，再求值：（x﹣1）（2x+1）﹣2（x﹣5）（x+2），其中x＝﹣2．

2、计算：．

3、图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

(1)观察图2，请你写出下列三个代数式（a+b）2，（a﹣b）2，ab之间的等量关系为　    ．

(2)运用你所得到的公式，计算：若m、n为实数，且mn＝﹣3，m﹣n＝4，试求m+n的值．

(3)如图3，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设AB＝8，两正方形的面积和S1+S2＝26，求图中阴影部分面积．

4、已知2m＝3，2n＝5．

(1)求2m+n的值；

(2)求22m-n的值．

5、请阅读下列材料：

我们可以通过以下方法求代数式的最小值．

∵

∴当x＝－4时，有最小值－3

请根据上述方法，解答下列问题：

(1)，则a＝______，b＝______；

(2)求证：无论x取何值，代数式的值都是正数：

(3)若代数式的最小值为4，求k的值．

-参考答案-

一、单选题

1、A

【解析】

【分析】

直接利用同底数幂的乘法运算法则计算得出答案．

【详解】

解：∵am=5，an=2，

∴a2m+n=×an=52×2=50．

故选：A．

【点睛】

此题主要考查了同底数幂的乘法运算，正确将原式变形是解题关键．

2、C

【解析】

【分析】

用科学记数法表示成的形式，其中，，代入可得结果．

【详解】

解：的绝对值大于表示成的形式

，

表示成

故选C．

【点睛】

本题考查了科学记数法．解题的关键在于确定的值．

3、A

【解析】

【分析】

利用积的乘方、幂的乘方把32n=6化成25n=6，2m=3化成2m+1=6，再比较求解即可．

【详解】

解：∵32n=6，

∴25n=6，

∵2m=3，

∴2m×2=3×2，即2m+1=6，

∴2m+1=25n，

∴m+1=5n，

故选：A．

【点睛】

本题主要考查了积的乘方、幂的乘方，关键是掌握计算法则，并能熟练应用．

4、B

【解析】

【分析】

分别根据同底数幂的乘法法则，幂的乘方运算法则，积的乘方运算法则以及同底数幂的除法法则逐一判断即可．

【详解】

、，故本选项不合题意；

B、，故本选项符合题意；

C、，故本选项不合题意；

D、，故本选项不合题意；

故选：B．

【点睛】

本题主要考查了同底数幂的乘除法以及幂的乘方与积的乘方，熟记幂的运算法则是解答本题的关键．

5、C

【解析】

【分析】

根据幂的乘方、积的乘方、单项式乘单项式、单项式乘多项式等知识，即可完成．

【详解】

A、，故计算错误；

B、，故计算错误；

C、，故计算正确；

D、，故计算错误．

故选：C

【点睛】

本题考查了幂的运算及整式的乘法，熟练掌握它们的运算法则是关键，但在单项式乘多项式中，千万不要漏乘．

6、B

【解析】

【分析】

先根据多项式乘以多项式法则展开，合并同类项，由题可得含x的平方的项的系数为0，求出a即可．

【详解】

解：（x2+ax+2）（2x-4）

=2x3+2ax2+4x-4x2-4ax-8

=2x3+（-4+2a）x2+（-4a+4）x-8，

∵（x2+ax+2）（2x-4）的结果中不含x2项，

∴-4+2a=0，

解得：a=2．

故选：B．

【点睛】

本题考查了多项式乘以多项式，能熟练地运用法则进行化简是解此题的关键．

7、C

【解析】

【分析】

结合题意，根据科学记数法的一般表达形式分析，即可得到答案．

【详解】

13657亿用科学记数法表示为

故选：C．

【点睛】

本题考查了科学记数法的知识，解题的关键是熟练掌握科学记数法的定义：任何绝对值大于1的数都可以用科学记数法表示为的形式，其中n为整数，且a满足1≤|a|<10．

8、D

【解析】

【分析】

根据平方项确定是完全平方公式，把公式展开，利用一次项系数相等确定m的值即可．

【详解】

解：∵x2 &#xF02B; mx &#xF02B; 4=（x±2）2=x2±4x+4，

∴m=±4．

故选D．

【点睛】

本题考查完全平方公式，掌握公式的特征是解题关键．

9、D

【解析】

【分析】

先观察题干实例的运算步骤，发现对应的数即为 从而可得出结论.

【详解】

解：由题意得：

故选D

【点睛】

本题考查的是利用完全平方公式进行运算，掌握“”是解本题的关键.

10、B

【解析】

【分析】

直接利用负整数指数幂的性质以及零指数幂的性质分别化简，进而比较大小得出答案．

【详解】

解：∵a＝（）﹣2，

b＝（）0＝1，

c＝（0.8）﹣1，

∴1，

∴a＞c＞b．

故选：B．

【点睛】

此题主要考查了负整数指数幂的性质以及零指数幂的性质，正确化简各数是解题关键．

二、填空题

1、4ab

【解析】

【分析】

组合后多出来的面积就是中间小正方形的面积，用大正方形减小正方形的得到原来长方形面积．

【详解】

∵为图2大正方形的面积；为小正方形面积，

∴为图1长方形面积

∴=2a×2b=4ab

故答案为：4ab

【点睛】

本题考查列代数式在求正方形面积中的应用，找到两者之差是图1长方形面积是关键．

2、±2

【解析】

【分析】

根据完全平方式的结构特征解决此题．

【详解】

解：x2﹣3kx+9＝x2﹣3kx+32．

∵x2﹣3kx+9是一个完全平方式，

∴﹣3kx＝±6x．

∴﹣3k＝±6．

∴k＝±2．

故答案为：±2．

【点睛】

本题考查完全平方式，熟知完全平方式的结构是解答的关键．

3、1

【解析】

【分析】

先把等号的左边根据多项式与多项式的乘法法则化简，然后与右边比较即可．

【详解】

解：∵，

∴，

∴，

∴a=2，2a-3=m，

∴m=1，

故答案为：1．

【点睛】

本题考查了多项式与多项式的乘法运算，多项式与多项式相乘，先用一个多项式的每一项分别乘另一个多项式的每一项，再把所得的积相加．

4、

【解析】

【分析】

由同类项的定义可得n=3，m=2，由单项式乘法法则计算即可得．

【详解】

∵由与是同类项

∴n=3，m=2

则

故答案为：

【点睛】

本题考查了同类项的定义以及单项式乘单项式的法则，这类题主要是根据同类项的定义：所含字母相同，并且相同字母的指数也分别相等的项叫做同类项.并建立方程（组）来解决问题，注意字母的顺序可能有变化．单项式乘单项式，把它们的系数、同底数幂分别向乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因事.

5、     a6    

【解析】

【分析】

根据同底数幂的乘法法则和积的乘方法则计算．

【详解】

解：a2·a4＝a6．

＝．

故答案为：a6；

【点睛】

本题考查了幂的运算，熟练掌握幂的运算法则是解答本题的关键．同底数的幂相乘，底数不变，指数相加；积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘．

三、解答题

1、5x+19，9

【解析】

【分析】

先计算多形式的乘法，再去括号合并同类项，然后把x＝﹣2代入计算．

【详解】

解：原式=2x2+x-2x-1-2(x2+2x-5x-10)

=2x2+x-2x-1-2x2-4x+10x+20

=5x+19，

当x＝﹣2时，

原式=-10+19=9

【点睛】

本题考查了整式的四则混合运算，熟练掌握运算顺序是解答本题的关键．四则混合运算的顺序是先算乘除，再算加减；同级运算，按从左到右的顺序计算．

2、2．

【解析】

【分析】

先计算零指数幂、负整数指数幂、算术平方根，再计算加减法即可得．

【详解】

解：原式

．

【点睛】

本题考查了零指数幂、负整数指数幂、算术平方根等知识点，熟练掌握各运算法则是解题关键．

3、 (1)（a+b）2=（a-b）2+4ab

(2)m+n=2或-2

(3)图中阴影部分面积为

【解析】

【分析】

（1）利用等面积法，大正方形面积等于阴影小正方形面积加上四个长方形面积，得到关系式；

（2）由（1）得到的关系式求解即可；

（3）设AC=m，BC=n，则m+n=8，m2+n2=26，由（1）得到的关系式求解即可．

(1)

解：由图形面积得（a+b）2=（a-b）2+4ab，

故答案为：（a+b）2=（a-b）2+4ab；

(2)

解：由（1）题所得（a+b）2=（a-b）2+4ab，

∴（m+n）2=（m-n）2+4mn，

∴当mn=-3，m-n=4时，

（m+n）2=42+4×（-3）=4，

∴m+n=2或-2；

(3)

解：设AC=m，BC=n，

则m+n=8，m2+n2=26，

又由（m+n）2=m2+2mn+n2，得

2mn=（m+n）2-（m2+n2）=64-26=38，

∴图中阴影部分的面积为：mn=．

【点睛】

本题考查了完全平方公式的几何意义，关键是能用算式表示图形面积并进行拓展应用．

4、故答案为：

【点睛】

本题考查完全平方公式，多项式乘以多项式，掌握完全平方公式的结构特征是正确解答的关键．

5．(1)15

(2)

【解析】

【分析】

（1）根据同底数幂的乘法的逆用可直接进行求解；

（2）根据题意易得，然后根据同底数幂的除法的逆用可直接进行求解．

(1)

解：∵2m＝3，2n＝5，

∴

(2)

解：∵2m＝3，2n＝5，

∴．

【点睛】

本题主要考查同底数幂的乘除法，熟练掌握同底数幂的乘除法的逆用是解题的关键．

5、 (1)3；1

(2)见解析

(3)

【解析】

【分析】

（1）将配方，然后与比较，即可求出a、b的值；

（2）先利用完全平方公式配方，再根据偶次方的非负性列式求解；

（3）二次项系数为1的二次三项式配方时，常数项为一次项系数一半的平方，故先将代数式提取公因数2，再配方，然后根据的最小值为4，可得关于k的方程，求解即可．

(1)

解：

而

所以a=3，b=1

故答案为：3；1

(2)

解：∵

无论x取何值，，

∴

∴无论x取何值，代数式的值都是正数．

(3)

解：

∵代数式有最小值4

∴

∴

∴

【点睛】

本题考查了配方法在最值问题与证明题中的应用，明确如何配方并读懂材料中的方法是解题的关键，配方法属于重要的运算方法之一，需熟练掌握．