【高频真题解析】2022年贵州省毕节市中考数学三年高频真题汇总 卷（Ⅲ）（含答案详解）

这是一份【高频真题解析】2022年贵州省毕节市中考数学三年高频真题汇总 卷（Ⅲ）（含答案详解），共27页。试卷主要包含了下列二次根式中，不能与合并的是等内容，欢迎下载使用。
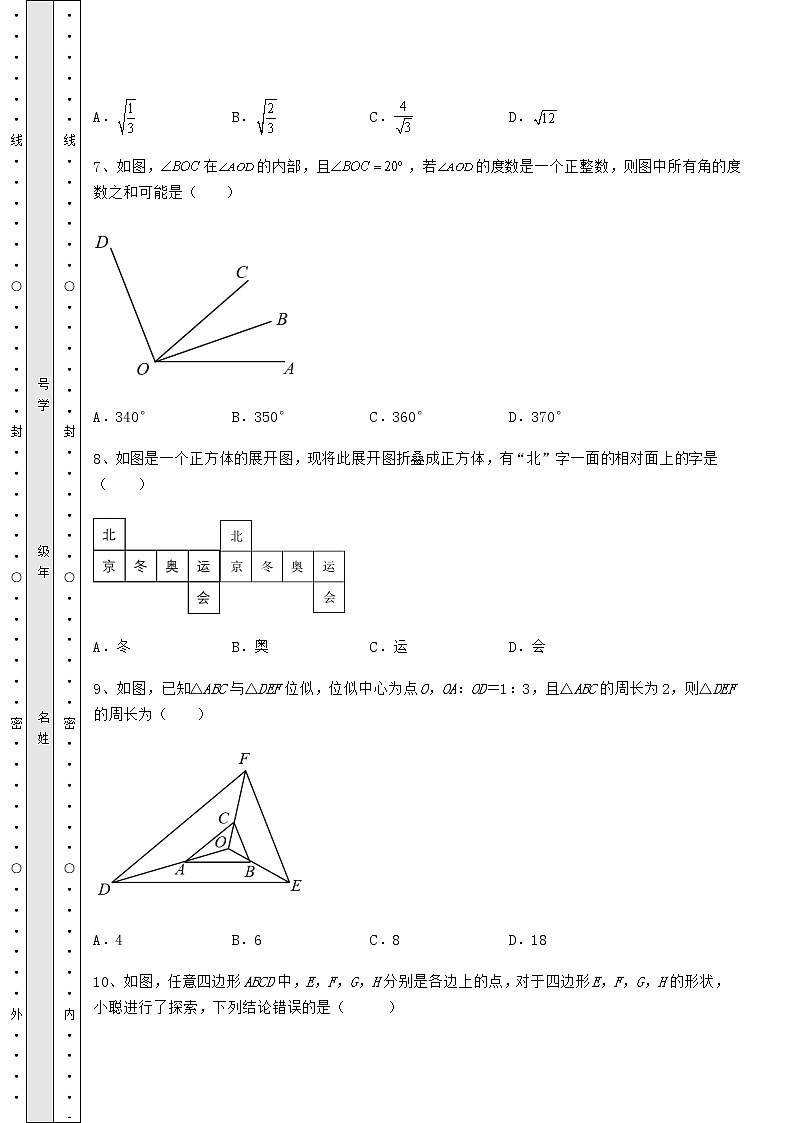
2022年贵州省毕节市中考数学三年高频真题汇总 卷（Ⅲ） 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、已知正五边形的边长为1，则该正五边形的对角线长度为（    ）．A． B． C． D．2、数学活动课上，同学们想测出一个残损轮子的半径，小宇的解决方案如下：如图，在轮子圆弧上任取两点A，B，连接，再作出的垂直平分线，交于点C，交于点D，测出的长度，即可计算得出轮子的半径．现测出，则轮子的半径为（    ）A． B． C． D．3、如图，表中给出的是某月的月历，任意选取“U”型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现这7个数的和不可能的是（    ）A．78 B．70 C．84 D．1054、在一次“寻宝”游戏中，寻宝人已经找到两个标志点和，并且知道藏宝地点的坐标是，则藏宝处应为图中的（    ）A．点 B．点 C．点 D．点5、如图，点 是 的角平分线 的中点， 点 分别在 边上，线段 过点 ， 且 ，下列结论中， 错误的是（    ）A． B． C． D．6、下列二次根式中，不能与合并的是（　　）A． B． C． D．7、如图，在的内部，且，若的度数是一个正整数，则图中所有角的度数之和可能是（    ）A．340° B．350° C．360° D．370°8、如图是一个正方体的展开图，现将此展开图折叠成正方体，有“北”字一面的相对面上的字是（    ）A．冬 B．奥 C．运 D．会9、如图，已知△ABC与△DEF位似，位似中心为点O，OA：OD＝1：3，且△ABC的周长为2，则△DEF的周长为（　　）A．4 B．6 C．8 D．1810、如图，任意四边形ABCD中，E，F，G，H分别是各边上的点，对于四边形E，F，G，H的形状，小聪进行了探索，下列结论错误的是（　　　）A．E，F，G，H是各边中点．且AC=BD时，四边形EFGH是菱形B．E，F，G，H是各边中点．且AC⊥BD时，四边形EFGH是矩形C．E，F，G，H不是各边中点．四边形EFGH可以是平行四边形D．E，F，G，H不是各边中点．四边形EFGH不可能是菱形第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，将一副三角板的直角顶点重合，摆放在桌面上，当∠AOC＝__________时，AB所在直线与CD所在直线互相垂直．2、若A（x，4）关于y轴的对称点是B（﹣3，y），则x=____，y=____．点A关于x轴的对称点的坐标是____．3、如图所示，在平面直角坐标系中，．在y轴找一点P，使得的周长最小，则周长最小值为_______4、如图，是体检时的心电图，其中横坐标表示时间，纵坐标表示心脏部位的生物电流，它们是两个变量．在心电图中， ___（填“是”或“不是” 的函数．5、如图，在边长1正网格中，A、B、C都在格点上，AB与CD相交于点D，则sin ∠ADC=_____．三、解答题（5小题，每小题10分，共计50分）1、如图，数轴上A和B．（1）点A表示         ，点B表示         ．（2）点C表示最小的正整数，点D表示的倒数，点E表示，在数轴上描出点C、D、E．（3）将该数轴上点A、B、C、D、E表示的数用“<”连起来：         ．2、郑州到西安的路程为480千米，由于西安疫情紧张，郑州物资中心对西安进行支援．甲乙两辆物资车分别从郑州和西安出发匀速行驶相向而行．甲车到西安后立即返回，已知乙车的速度为每小时，且到郑州后停止行驶，进行消毒．它们离各自出发地的距离与行驶时间之间的关系如下图所示．（1）______，______．（2）请你求出甲车离出发地郑州的距离与行驶时间之间的函数关系式．（3）求出点的坐标，并说明此点的实际意义．（4）直接写出甲车出发多长时间两车相距40千米．3、如图，有一块直角三角形纸片，两直角边cm，cm，现将直角边AC沿直线AD对折，使它落在斜边AB上，且与AE重合，求CD的长．4、如图，在平面直角坐标系xOy中，抛物线与x轴交于点A（-1，0）和点B（3，0），与y轴交于点C，顶点为点D．（1）求该抛物线的表达式及点C的坐标；（2）联结BC、BD，求∠CBD的正切值；（3）若点P为x轴上一点，当△BDP与△ABC相似时，求点P的坐标．5、如图，AC，BD相交于的点O，且∠ABO＝∠C．求证：△AOB∽△DOC． -参考答案-一、单选题1、C【分析】如图，五边形ABCDE为正五边形， 证明 再证明可得：设AF=x，则AC=1+x，再解方程即可.【详解】解：如图，五边形ABCDE为正五边形， ∴五边形的每个内角均为108°，  ∴∠BAG=∠ABF=∠ACB=∠CBD= 36°， ∴∠BGF=∠BFG=72°，  设AF=x，则AC=1+x， 解得：，经检验：不符合题意，舍去， 故选C【点睛】本题考查的是正多边形的性质，等腰三角形的判定与性质，相似三角形的判定与性质，证明是解本题的关键.2、C【分析】由垂径定理，可得出BC的长；连接OB，在Rt△OBC中，可用半径OB表示出OC的长，进而可根据勾股定理求出得出轮子的半径即可．【详解】解：设圆心为O，连接OB．Rt△OBC中，BC=AB=20cm，根据勾股定理得：OC2+BC2=OB2，即：（OB-10）2+202=OB2，解得：OB=25；故轮子的半径为25cm．故选：C．【点睛】本题考查垂径定理，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．3、A【分析】设“U”型框中的最下排正中间的数为x，则其它6个数分别为x-15，x-8，x-1，x+1，x-6，x-13，表示出这7个数之和，然后分别列出方程解答即可．【详解】解：设“U”型框中的最下排正中间的数为x，则其他6个数分别为x-15，x-8，x-1，x+1，x-6，x-13，这7个数之和为：x-15+x-8+x-1+x+1+x-6+x-13=7x-42．由题意得：A、7x-42=78，解得x=，不能求出这7个数，符合题意；B、7x-42=70，解得x=16，能求出这7个数，不符合题意；C、7x-42=84，解得x=18，能求出这7个数，不符合题意；D、7x-42=105，解得x=21，能求出这7个数，不符合题意．故选：A．【点睛】本题考查一元一次方程的实际运用，掌握“U”型框中的7个数的数字的排列规律是解决问题的关键．4、B【分析】结合题意，根据点的坐标的性质，推导得出原点的位置，再根据坐标的性质分析，即可得到答案．【详解】∵点和，∴坐标原点的位置如下图：∵藏宝地点的坐标是∴藏宝处应为图中的：点故选：B．【点睛】本题考查了坐标与图形，解题的关键是熟练掌握坐标的性质，从而完成求解．5、D【分析】根据AG平分∠BAC，可得∠BAG=∠CAG，再由点 是 的中点，可得 ，然后根据，可得到△DAE∽△CAB，进而得到△EAF∽△BAG，△ADF∽△ACG，即可求解．【详解】解：∵AG平分∠BAC，∴∠BAG=∠CAG，∵点 是 的中点，∴ ，∵，∠DAE=∠BAC，∴△DAE∽△CAB，∴ ，∴∠AED=∠B，∴△EAF∽△BAG，∴ ，故C正确，不符合题意；∵，∠BAG=∠CAG，∴△ADF∽△ACG，∴ ，故A正确，不符合题意；D错误，符合题意；∴，故B正确，不符合题意；故选：D【点睛】本题主要考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质定理是解题的关键．6、B【分析】先把每个选项的二次根式化简，再逐一判断与的被开方数是否相同，被开方数相同则能合并，不相同就不能合并，从而可得答案.【详解】解：能与合并， 故A不符合题意；不能与合并，故B不符合题意；能与合并， 故C不符合题意；能与合并， 故D不符合题意；故选B【点睛】本题考查的是同类二次根式的概念，掌握“同类二次根式的概念进而判断两个二次根式能否合并”是解本题的关键.7、B【分析】根据角的运算和题意可知，所有角的度数之和是∠AOB+∠BOC+∠COD+∠AOC+∠BOD+∠AOD，然后根据，的度数是一个正整数，可以解答本题．【详解】解：由题意可得，图中所有角的度数之和是∠AOB+∠BOC+∠COD+∠AOC+∠BOD+∠AOD=3∠AOD+∠BOC∵，的度数是一个正整数，∴A、当3∠AOD+∠BOC＝340°时，则= ，不符合题意；B、当3∠AOD+∠BOC＝3×110°+20°＝350°时，则=110°，符合题意；C、当3∠AOD+∠BOC＝360°时，则=，不符合题意；D、当3∠AOD+∠BOC＝370°时，则=，不符合题意．故选：B．【点睛】本题考查角度的运算，解题的关键是明确题意，找出所求问题需要的条件．8、D【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“京”与“奥”是相对面，“冬”与“运”是相对面，“北”与“会”是相对面．故选：D．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．9、B【分析】由与是位似图形，且知与的位似比是，从而得出周长：周长，由此即可解答．【详解】解：∵与是位似图形，且，与的位似比是．则周长：周长，∵△ABC的周长为2，∴周长故选：B．【点睛】本题考查了位似变换：位似图形的任意一对对应点与位似中心在同一直线上，它们到位似中心的距离之比等于相似比，位似是相似的特殊形式，位似比等于相似比，其对应的周长比等于相似比．10、D【分析】当为各边中点，，，四边形是平行四边形；A中AC=BD，则，平行四边形为菱形，进而可判断正误；B中AC⊥BD，则，平行四边形为矩形，进而可判断正误；E，F，G，H不是各边中点，C中若四点位置满足，则可知四边形EFGH可以是平行四边形，进而可判断正误；D中若四点位置满足，则可知四边形EFGH可以是菱形，进而可判断正误．【详解】解：如图，连接当为各边中点时，可知分别为的中位线∴∴四边形是平行四边形A中AC=BD，则，平行四边形为菱形；正确，不符合题意；B中AC⊥BD，则，平行四边形为矩形；正确，不符合题意；C中E，F，G，H不是各边中点，若四点位置满足，则可知四边形EFGH可以是平行四边形；正确，不符合题意；D中若四点位置满足，则可知四边形EFGH可以是菱形；错误，符合题意；故选D．【点睛】本题考查了平行四边形、菱形、矩形的判定，中位线等知识．解题的关键在于熟练掌握特殊平行四边形的判定．二、填空题1、105°或75°【分析】分两种情况：①AB⊥CD，交DC延长线于E，OB交DC延长线于F，②AB⊥CD于G，OA交DC于H求出答案．【详解】解：①如图1，AB⊥CD，交DC延长线于E，OB交DC延长线于F，∵∠B=45°，∠BEF=90°，∴∠CFO=∠BFE=45°，∵∠DCO=60°，∴∠COF=15°∴∠AOC=90°+15°=105°；②如图2，AB⊥CD于G，OA交DC于H，∵∠A=45°，∠AGH=90°，∴∠CHO=∠AHG=45°，∵∠DCO=60°，∴∠AOC=180°-60°-45°=75°；故答案为：105°或75°．【点睛】此题考查了三角形的角度计算，正确掌握三角板的度数及各角度的关系是解题的关键．2、3    4    (3，﹣4)    【分析】根据点关于x轴对称则横坐标不变纵坐标互为相反数，关于y轴对称则纵坐标不变横坐标互为相反数即可求解．【详解】解：∵A(x，4)关于y轴的对称点是B(-3，y)，∴x=3，y=4，∴A点坐标为(3，4)，∴点A关于x轴的对称点的坐标是(3，-4)．故答案为：3；4；(3，-4)．【点睛】本题考查了点关于坐标轴对称的特点：点关于x轴对称则横坐标不变纵坐标互为相反数，关于y轴对称则纵坐标不变横坐标互为相反数，由此即可求解．3、【分析】作点B关于y轴的对称点C，连接AC，与y轴的交点即为满足条件的点P，由勾股定理求出AC、AB的长，即可求得周长最小值．【详解】作点B关于y轴的对称点C，则点C的坐标为，连接AC，与y轴的交点即为满足条件的点P，如图所示由对称的性质得：PB=PC∴AB+PA+PB=AB+PA+PC≥AB+AC即当点P在AC上时，周长最小，且最小值为AB+AC由勾股定理得：，∴周长最小值为故答案为：【点睛】本题考查了点与坐标，两点间距离最短，对称的性质，勾股定理等知识，作点关于x轴的对称点是关键．4、是【分析】根据函数的定义判断即可．【详解】解：两个变量和，变量随的变化而变化，且对于每一个，都有唯一值与之对应，是的函数．故答案为：是．【点睛】本题考查了函数的理解即两个变量和，变量随的变化而变化，且对于每一个，都有唯一值与之对应,正确理解定义是解题的关键．5、##【分析】将转化成其他相等的角，在直角三角形中，利用正弦函数值的定义求解即可．【详解】解：延长CD交正方形的另一个顶点为，连接BE，如下图所示：由题意可知：，，根据正方形小格的边长及勾股定理可得：，，在中，，，故答案为：．【点睛】本题主要是考查了勾股定理和求解正弦值，熟练地找到所求角在的直角三角形，利用正弦函数值的定义进行求解，这是解决该题的关键．三、解答题1、（1），（2）见解析（3）1＜＜＜＜【分析】（1）根据数轴直接写出A、B所表示的数即可；（2）根据最小的正整数是1，的倒数是，然后据此在数轴上找到C、D、E即可；（3）将A、B、C、D、E表示的数从小到大排列，再用 “＜”连接即可．（1）解：由数轴可知A、B表示的数分别是：，．故答案为：，．（2）解：∵最小的正整数是1，的倒数是∴C表示的数是1，D表示的数是，∴如图：数轴上的点C、D、E即为所求．（3）解：根据（2）的数轴可知，将点A、B、C、D、E表示的数用“<”连接如下：1＜＜＜＜．【点睛】本题主要考查了在数轴上表示数、倒数、最小的正整数、倒数以及利用数轴比较有理数的大小，在数轴上正确表示有理数成为解答本题的关键．2、（1）8，6.5（2）（3）点P的坐标为（5，360），点P的实际意义是：甲车在行驶5小时后，甲乙两车分别距自己的出发地的距离为360千米（4）当甲车出发2.4小时或2.8小时或小时两车相距40千米【分析】（1）先根据题意判断出直线的函数图像时乙车的，折线的函数图像时甲车的，然后求出甲车的速度即可求出甲返回郑州的时间，即可求出m；然后算出乙车从西安到郑州需要的时间即可求出n；（2）分甲从郑州到西安和从西安到郑州两种情况求解即可；（3）根据函数图像可知P点代表的实际意义是：在P点时，甲乙两车距自己的出发地的距离相同，由此列出方程求解即可；（4）分情况：当甲车在去西安的途中，甲乙两车相遇前，当甲车在去西安的途中，甲乙两车相遇后，当甲车在返回郑州的途中，乙未到郑州时，当甲车在返回郑州的途中，乙已经到郑州时，四种情况讨论求解即可．（1）解：∵甲乙两辆物资车分别从郑州和西安出发匀速行驶相向而行．甲车到西安后立即返回，乙车到底郑州后立即停止，∴直线的函数图像是乙车的，折线的函数图像是甲车的，由函数图像可知，甲车4小时从郑州行驶到西安走了480千米，∴甲车的速度=480÷4=120千米/小时，∴甲车从西安返回郑州需要的时间=480÷120=4小时，∴m=4+4=8；∵乙车的速度为80千米/小时，∴乙车从西安到达郑州需要的时间=480÷80=6小时，∵由函数图像可知乙车是在甲车出发0.5小时后出发，∴n=0.5+6=6.5，故答案为：8，6.5；（2）解：当甲车从郑州去西安时，∵甲车的速度为120千米/小时，∴甲车与郑州的距离，当甲车从西安返回郑州时，∵甲车的速度为120千米/小时，∴甲车与郑州的距离，∴；（3）解：根据函数图像可知P点代表的实际意义是：在P点时，甲乙两车距自己的出发地的距离相同，∵此时甲车处在返程途中，∴，解得，∴，∴点P的坐标为（5，360），∴点P的实际意义是：甲车在行驶5小时后，甲乙两车分别距自己的出发地的距离为360千米；（4）解：当甲车在去西安的途中，甲乙两车相遇前，由题意得：，解得；当甲车在去西安的途中，甲乙两车相遇后，由题意得：，解得；当甲车在返回郑州的途中，乙未到郑州时，由题意得：解得（不符合题意，舍去），当甲车在返回郑州的途中，乙已经到郑州时，由题意得：解得；综上所述，当甲车出发2.4小时或2.8小时或小时两车相距40千米．【点睛】本题主要考查了从函数图像获取信息，一元一次方程的应用，正确理解题意是解题的关键．3、CD长为3cm【分析】在中，由勾股定理得，由折叠对称可知，cm，，，设，则，在中，由勾股定理得，计算求解即可．【详解】解：∵cm，cm∴在中， 由折叠对称可知，cm，∴cm设，则∴在中，由勾股定理得即解得∴CD的长为3cm．【点睛】本题考查了轴对称，勾股定理等知识．解题的关键在于找出线段的数量关系．4、（1），点C的坐标为（0，-3）（2）（3）（-3，0）或（-，0）【分析】（1）把A、B两点坐标代入函数求出b，c的值即可求函数表达式；再令x=0，求出y从而求出C点坐标；（2）先求B、C、D三点坐标，再求证△BCD为直角三角形，再根据正切的定义即可求出；（3）分两种情况分别进行讨论即可．（1）解：（1）将A（-1，0）、B（3，0）代入，得   解得： 所以，． 当x=0时，．∴点C的坐标为（0，-3）．（2）解：连接CD，过点D作DE⊥y轴于点E，∵，∴点D的坐标为（1，-4）． ∵B（3，0）、C（0，-3）、D（1，-4），E（0，-4），∴OB=OC=3，CE=DE=1，∴BC=，DC=，BD=．∴． ∴∠BCD=90°． ∴tan∠CBD=． （3）解：∵tan∠ACO=，∴∠ACO=∠CBD． ∵OC =OB，∴∠OCB=∠OBC=45°．∴∠ACO+∠OCB =∠CBD+∠OBC．即：∠ACB =∠DBO． ∴当△BDP与△ABC相似时，点P在点B左侧．（i）当时，∴．∴BP=6．∴P（-3，0）． （ii）当时，∴．∴BP=．∴P（-，0）． 综上，点P的坐标为（-3，0）或（-，0）．【点睛】本题是二次函数的综合题，掌握相关知识是解题的关键．5、见解析【分析】利用对顶角相等得到∠AOB=∠COD，再结合已知条件及相似三角形的判定定理即可求解．【详解】证明：∵AC，BD相交于的点O，∴∠AOB＝∠DOC，又∵∠ABO＝∠C，∴△AOB∽△DOC．【点睛】本题考查了相似三角形的判定定理：若一对三角形的两组对应角相等，则这两个三角形相似，由此即可求解．