高中人教B版 (2019)7.2.4 诱导公式第1课时学案

7．2.4　诱导公式

第1课时　诱导公式(一)

[课程目标] 1.借助单位圆的直观性探索正弦、余弦和正切的诱导公式．

2．掌握正弦、余弦和正切的诱导公式的应用．

3．通过对公式的运用，提高三角恒等变形的能力和渗透化归数学思想，提高分析问题、解决问题的能力．

[填一填]

1．诱导公式①

终边相同的角的同名三角函数值相等．

即：cos(α＋k· 2π)＝cosα，sin(α＋k·2π)＝sinα，tan(α＋k·2π)＝tanα.

其作用是把绝对值大于2π的任意角的三角函数值化为[0,2π)上的角的同名三角函数值．

2．诱导公式②

角－α的三角函数等于角α的同名三角函数，前边放上把α看作锐角时，－α所在象限的原三角函数值的符号．即

cos(－α)＝cosα，sin(－α)＝－sinα，

tan(－α)＝－tanα.

其作用是把任意负角的三角函数转化为正角的三角函数．

3．诱导公式③

角π－α的三角函数等于角α的同名三角函数，前边放上把角α看作锐角时，π－α所在象限的原三角函数值的符号，即

sin(π－α)＝sinα，cos(π－α)＝－cosα，tan(π－α)＝－tanα.

4．诱导公式④

角π＋α的三角函数等于角α的同名三角函数，前边放上把角α看作锐角时，π－α所在象限的原三角函数值的符号，即

sin(π＋α)＝－sinα，cos(π＋α)＝－cosα，tan(π＋α)＝tanα.

[答一答]

1．对四组诱导公式的理解应注意什么问题？

提示：(1)公式①的作用是：其一，可以将任意角的正弦、余弦、正切函数值，分别化为0°到360°的角的同一三角函数值(方法是先在0°到360°的范围内找出与它终边相同的角，再把它写成公式①的形式，然后得出结果)；其二，便于研究这三种三角函数的周期性．

(2)公式②和③和④的推导，要紧扣点P(x，y)关于坐标轴和关于原点的对称性，而且点P是角α的终边与单位圆的交点．于是P(x，y)可以写为P(cosα，sinα)，P点关于x轴的对称为P′(cosα，－sinα)，P点关于原点的对称点为P″(－cosα，－sinα)，由此推导出诱导公式②.

关于诱导公式③，最主要的是α与π－α的三角函数间的关系，即

sin(π－α)＝sinα，cos(π－α)＝－cosα.

tan(π－α)＝－tanα.

将上面的三个公式与诱导公式①联合起来，就得到诱导公式④.由诱导公式②③又得到关于α与π＋α这两个互补的角的关系式：

sin(α＋π)＝－sinα，cos(α＋π)＝－cosα，

tan(α＋π)＝tanα.

这是将公式③中的－α换成α以后得到的结果．

(3)这一组公式的共同特点：角－α，2kπ＋α(k∈Z)，π＋α，π－α的三角函数等于角α的同名三角函数，前边放上把角α看成锐角时，该角所在象限的原三角函数值的符号，口诀为：“函数名不变，符号看象限”．

(4) 三角函数的诱导公式是圆的对称性的“代数表示”，因此，用数形结合的思想从单位圆关于坐标轴、直线y＝x、原点等的对称性出发研究诱导公式，可以发现终边分别关于原点或坐标轴对称的角的三角函数值之间的关系，使得诱导公式(数)与单位圆(形)得到紧密结合，成为一个整体．

2．运用诱导公式求任意角的三角函数值的步骤是怎样的？

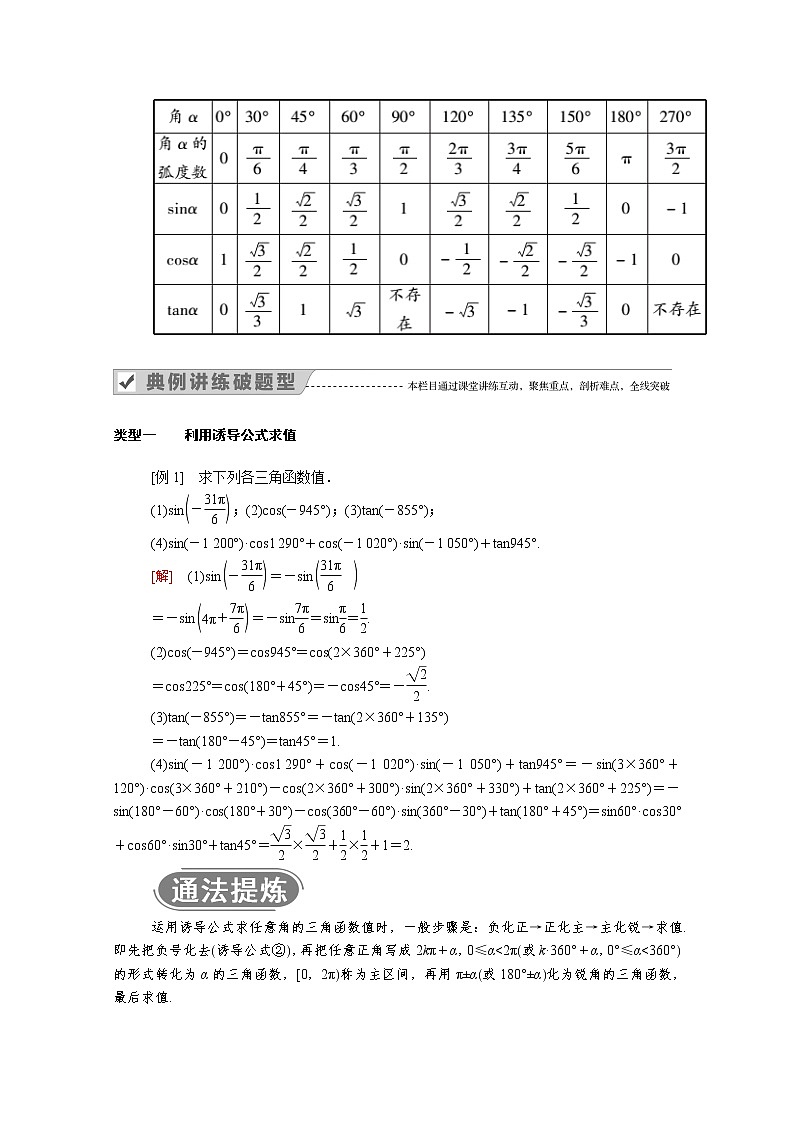
3．常用的特殊角的三角函数值有哪些？

提示：

类型一　　利用诱导公式求值

[例1]　求下列各三角函数值．

(1)sin；(2)cos(－945°)；(3)tan(－855°)；

(4)sin(－1 200°)·cos1 290°＋cos(－1 020°)·sin(－1 050°)＋tan945°.

[解]　(1)sin＝－sin

＝－sin＝－sin＝sin＝.

(2)cos(－945°)＝cos945°＝cos(2×360°＋225°)

＝cos225°＝cos(180°＋45°)＝－cos45°＝－.

(3)tan(－855°)＝－tan855°＝－tan(2×360°＋135°)

＝－tan(180°－45°)＝tan45°＝1.

(4)sin(－1 200°)·cos1 290°＋cos(－1 020°)·sin(－1 050°)＋tan945°＝－sin(3×360°＋120°)·cos(3×360°＋210°)－cos(2×360°＋300°)·sin(2×360°＋330°)＋tan(2×360°＋225°)＝－sin(180°－60°)·cos(180°＋30°)－cos(360°－60°)·sin(360°－30°)＋tan(180°＋45°)＝sin60°·cos30°＋cos60°·sin30°＋tan45°＝×＋×＋1＝2.

运用诱导公式求任意角的三角函数值时，一般步骤是：负化正→正化主→主化锐→求值.即先把负号化去诱导公式②，再把任意正角写成2kπ＋α，0≤α<2π或k·360°＋α，0°≤α<360°的形式转化为α的三角函数，[0，2π称为主区间，再用π±α或180°±α化为锐角的三角函数，最后求值.

[变式训练1]　计算：

(1)sin405°·cos(－765°)；

(2)sin·tanπ－cosπ·tan.

解：(1)原式＝sin(360°＋45°)·cos765°

＝sin45°·cos(2×360°＋45°)

＝sin45°·cos45°＝×＝.

(2)原式＝·tan－cos·tan

＝－sin·tan－cos·tan

＝－××－×(－1)＝0.

类型二　　条件求值

[例2]　已知cos＝，求cos－sin2的值．

[解]　∵cos＝cos

＝－cos＝－，

sin2＝sin2

＝1－cos2＝1－2＝，

∴cos－sin2

＝－－＝－.

1解决条件求值问题，首先要仔细观察条件与所求式之间的角、函数名及有关运算之间的差异及联系.

2可以将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化.

[变式训练2]　已知cos(α－75°)＝－，且α为第四象限角，求sin(105°＋α)的值．

解：∵cos(α－75°)＝－<0，且α为第四象限角，

∴α－75°是第三象限角．

∴sin(α－75°)＝－

＝－＝－.

∴sin(105°＋α)＝sin[180°＋(α－75°)]

＝－sin(α－75°)＝.

类型三　　三角函数式的化简

[例3]　化简.

[分析]　由于本例含有根式且所给角度不一样，化简时应用诱导公式尽可能将角统一，去根号时还应注意三角函数的正负．

[解]　原式＝

＝＝

＝＝－1.

1.三角函数式的化简常用诱导公式将任意角的三角函数转化为锐角的三角函数.

2.化简时要特别注意“1”的变式应用.

[变式训练3]　化简：－(n∈Z)．

解：原式＝＋

＝＋＝－cosα＋

＝－cosα－cos2α.

类型四　　三角函数式的证明

[例4]　求证：＝tanθ.

[分析]　运用诱导公式①②，尝试从等式的左边入手，直至推出右边即可．

[证明]　左边＝

＝＝tanθ＝右边．

∴原等式成立．

1.用从等式的一边开始化为等式的另一边的方法证明恒等式问题，实质上就是三角函数式的化简问题.

2.证明三角恒等式的一般思路是：先分析角的特点及角之间的关系，再将角变形，然后利用诱导公式及同角三角函数的基本关系式来完成证明.

[变式训练4]　设tan＝a.

求证：＝.

证明：

左边＝

＝

＝＝＝右边．

∴等式成立.

1．cos300°＝(　C　)

A．－   B．－

C.   D.

解析：该题考查三角函数的诱导公式和特殊角的三角函数值．cos300°＝cos(360°－60°)＝cos(－60°)＝cos60°＝，故选C.

2．已知sin＝m，则cos的值等于(　C　)

A．m   B．－m

C.   D．－

解析：∵sin＝sin＝sin，

∴sin＝m，且∈，∴cos＝.

3.等于(　A　)

A．sin2－cos2   B．sin2＋cos2

C．±(sin2－cos2)   D．cos2－sin2

解析：∵<2<π，∴sin2>cos2，即sin2－cos2>0，

∴＝

＝＝|sin2－cos2|＝sin2－cos2.

4．已知cos＝，则cos＝.

解析：∵－θ＋＋θ＝2π，

∴－θ＝2π－，

∴cos

＝cos

＝cos＝.