高考数学(理数)一轮复习课时作业20《三角函数的图象与性质》(原卷版)

这是一份高考数学(理数)一轮复习课时作业20《三角函数的图象与性质》(原卷版)，共4页。试卷主要包含了定义运算等内容，欢迎下载使用。
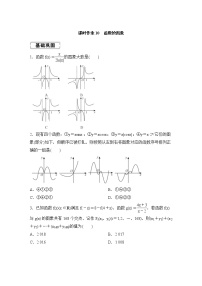
课时作业20　三角函数的图象与性质1．在函数①y＝cos|2x|，②y＝|cosx|，③y＝cos，④y＝tan中，最小正周期为π的所有函数为(　　)A．①②③   B．①③④C．②④   D．①③2．关于函数y＝tan，下列说法正确的是(　　)A．是奇函数 B．在区间上单调递减C．为其图象的一个对称中心D．最小正周期为π3．若是函数f(x)＝sinωx＋cosωx图象的一个对称中心，则ω的一个取值是(　　)A．2   B．4C．6   D．84．已知x0＝是函数f(x)＝sin(2x＋φ)的一个极大值点，则f(x)的一个单调递减区间是(　　)A．   B．C．   D．5．已知函数f(x)＝2sin(2x＋φ)的图象过点(0，)，则f(x)图象的一个对称中心是(　　)A．   B．C．   D．6．定义运算：a*b＝例如1](　　)A．   B．[－1,1]C．   D．7．已知函数f(x)＝2cos(ωx＋φ)＋1，其图象与直线y＝3相邻两个交点的距离为，若f(x)＞1对任意x∈恒成立，则φ的取值范围是(　　)A．   B．C．   D．8．若函数f(x)＝cos(0＜φ＜π)是奇函数，则φ＝        .9．已知关于x的方程2sin＋1－a＝0在区间上存在两个根，则实数a的取值范围是        ．10．设函数f(x)＝3sin，若存在这样的实数x1，x2，对任意的x∈R，都有f(x1)≤f(x)≤f(x2)成立，则|x1－x2|的最小值为        _.11．已知函数f(x)＝sin(ωx＋φ)的图象关于直线x＝对称，且图象上相邻两个最高点的距离为π.(1)求ω和φ的值；(2)若f＝，求cos的值．    12．已知f(x)＝sin.(1)求函数f(x)图象的对称轴方程；(2)求f(x)的单调递增区间；(3)当x∈时，求函数f(x)的最大值和最小值．       13．已知函数f(x)＝sin(2x＋φ)，其中φ为实数，若f(x)≤对任意x∈R恒成立，且f＞0，则f(x)的单调递减区间是(　　)A．(k∈Z)         B．(k∈Z)C．(k∈Z)     D．(k∈Z)14．设ω∈N*且ω≤15，则使函数y＝sinωx在区间上不单调的ω的个数是(　　)A．6   B．7C．8   D．915．若函数f(x)＝Acos2(ωx＋φ)＋1的最大值为3，f(x)的图象与y轴的交点坐标为(0,2)，其相邻两条对称轴间的距离为2，则f(1)＋f(2)＋…＋f(2 018)＝        .   16．已知函数f(x)＝2sin2－cos2x－1，x∈R.(1)求f(x)的最小正周期；(2)若h(x)＝f(x＋t)的图象关于点对称，且t∈(0，π)，求t的值；(3)当x∈时，不等式|f(x)－m|＜3恒成立，求实数m的取值范围．