高考数学(理数)一轮复习课时作业59《算法与程序框图》(原卷版)

这是一份高考数学(理数)一轮复习课时作业59《算法与程序框图》(原卷版)，共8页。试卷主要包含了如图是一个算法等内容，欢迎下载使用。
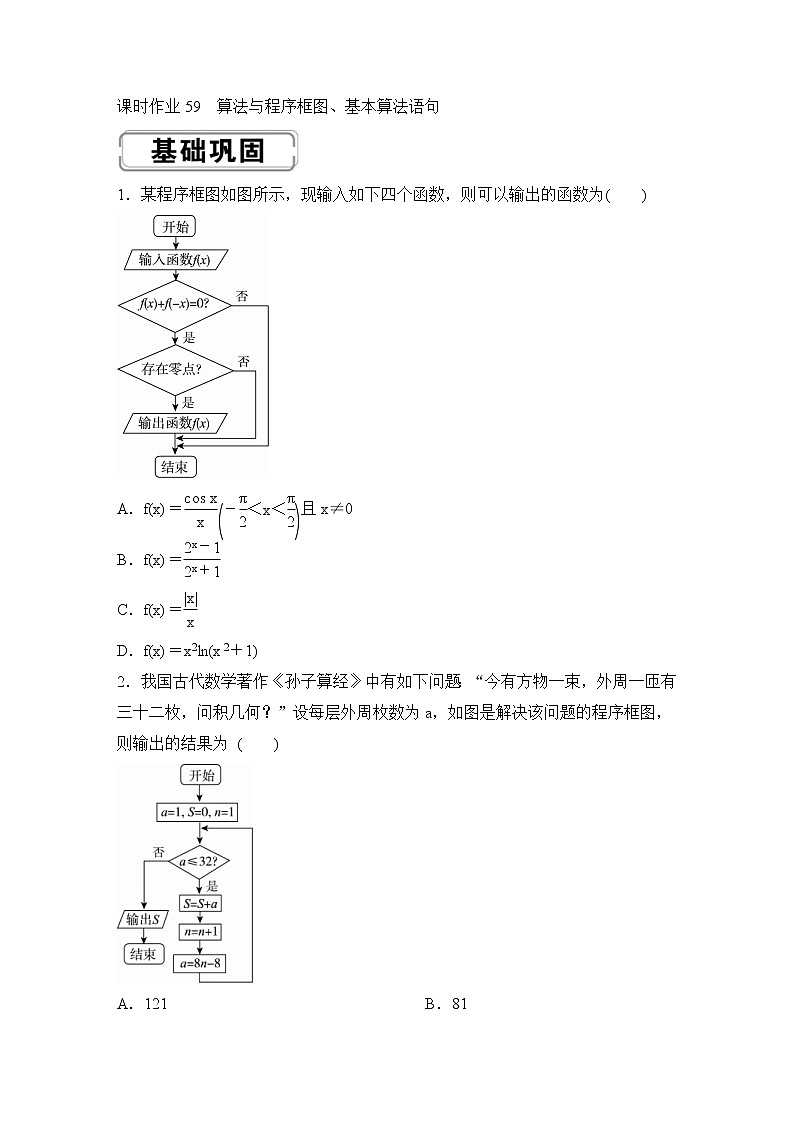
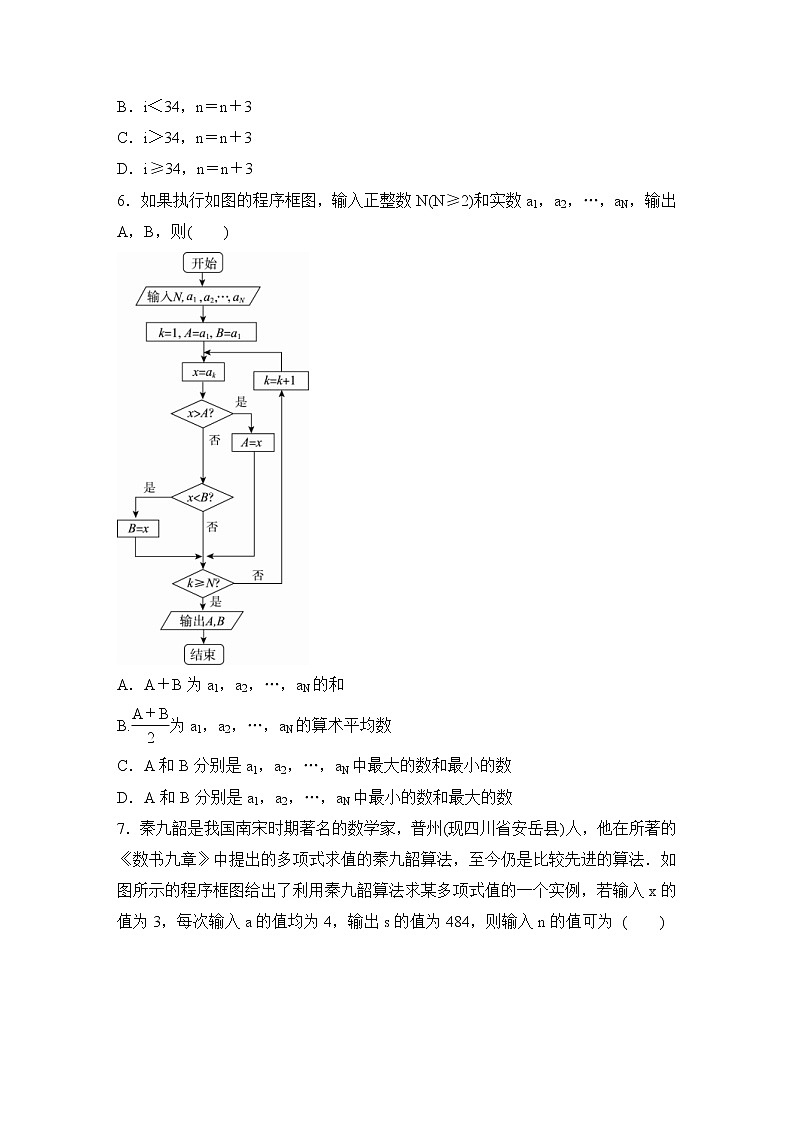
课时作业59　算法与程序框图、基本算法语句1．某程序框图如图所示，现输入如下四个函数，则可以输出的函数为(　　)A．f(x)＝且x≠0B．f(x)＝C．f(x)＝D．f(x)＝x2ln(x2＋1)2．我国古代数学著作《孙子算经》中有如下问题：“今有方物一束，外周一匝有三十二枚，问积几何？”设每层外周枚数为a，如图是解决该问题的程序框图，则输出的结果为 (　　)A．121    B．81C．74    D．493．执行如图所示的程序框图，如果输出的k的值为3，则输入的a的值可以是 (　　)A．20　　　　B．21C．22　　　　D．234．根据如图算法语句，当输入x为60时，输出y的值为(　　)A．25　　　　 B．30  C．31　　　　 D．615．如图，给出的是计算1＋＋＋…＋的值的一个程序框图，则图中判断框内(1)处和执行框中的(2)处应填的语句是(　　)A．i＞100，n＝n＋1B．i＜34，n＝n＋3C．i＞34，n＝n＋3D．i≥34，n＝n＋36．如果执行如图的程序框图，输入正整数N(N≥2)和实数a1，a2，…，aN，输出A，B，则(　　)A．A＋B为a1，a2，…，aN的和B.为a1，a2，…，aN的算术平均数C．A和B分别是a1，a2，…，aN中最大的数和最小的数D．A和B分别是a1，a2，…，aN中最小的数和最大的数7．秦九韶是我国南宋时期著名的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为3，每次输入a的值均为4，输出s的值为484，则输入n的值可为 (　　)A．6    B．5C．4    D．38．执行两次如图所示的程序框图，若第一次输入的x的值为7，第二次输入的x的值为9，则第一次、第二次输出的a的值分别为(　　)A．0,0B．1,1C．0,1D．1,09．如图是一个算法流程图．若输入x的值为，则输出y的值是        .10．执行如图所示的程序框图，若输入的a，b的值分别为0和9，则输出的i的值为        .11．程序框图如图，若输入的S＝1，k＝1，则输出的S为        .12．公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为        .(参考数据：sin 15°≈0.258 8，sin 7.5°≈0.130 5)13．如图(1)是某县参加2017年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1，A2，…，A10(如A2表示身高(单位：cm)在[150,155)内的学生人数)．图(2)是统计图(1)中身高在一定范围内学生人数的一个程序框图．现要统计身高在160～180 cm(含160 cm，不含180 cm)的学生人数，则在流程图中的判断框内应填写(　　)图(1)　图(2)A．i＜6?    B．i＜7?C．i＜8?    D．i＜9?14．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思：一尺的木棍，每天截取一半，永远都截不完．现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位：尺)，则①②③处可分别填入的语句是 (　　)A．i＜7，s＝s－，i＝2i    B．i≤7，s＝s－，i＝2iC．i＜7，s＝，i＝i＋1    D．i≤7，s＝，i＝i＋115．如图是“二分法”求方程近似解的流程图，在①，②处应填写的内容分别是  (　　)A．f(a)·f(m)＜0？；b＝m    B．f(b)·f(m)＜0？；b＝mC．f(a)·f(m)＜0？；m＝b    D．f(b)·f(m)＜0？；m＝b16．执行如图所示的程序框图，则输出的结果为        .