












所属成套资源:2022人教版数学四年级下册同步PPT课件+教案+同步练习
小学数学人教版四年级下册乘法运算定律一等奖课件ppt
展开
这是一份小学数学人教版四年级下册乘法运算定律一等奖课件ppt,文件包含人教版数学四下322乘法分配律课件pptx、人教版数学四下322乘法分配律教案docx、人教版数学四下322乘法分配律-同步练习2附答案docx、人教版数学四下322乘法分配律-同步练习1附答案docx等4份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
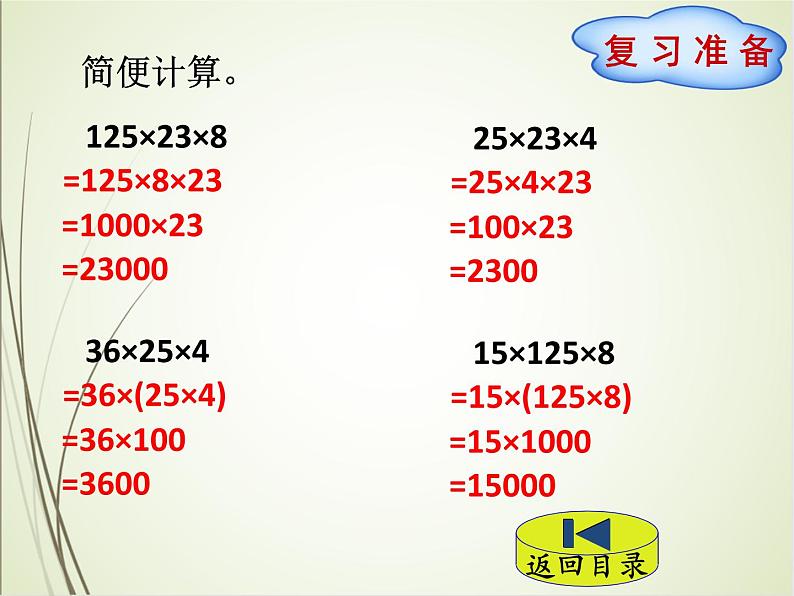
第课时 乘法分配律1.通过观察、分析、比较,引导学生概括出乘法分配律,理解并且掌握乘法分配律。2.能运用乘法分配律进行简便计算。3.培养学生的分析推理能力,培养学生的符号感,抽象概括能力。【重点】 在解决实际问题的过程中发现并理解乘法分配律。【难点】 自主发现规律,抽象归纳,并能用符号语言或其他方式与同伴交流规律。【教师准备】 PPT课件。【学生准备】 学习单。 简便计算。125×23×8 25×23×436×25×4 15×125×8【参考答案】125×23×8
=125×8×23
=1000×23
=2300025×23×4
=25×4×23
=100×23
=2300 36×25×4
=36×(25×4)
=36×100
=360015×125×8
=15×(125×8)
=15×1000
=15000方法一一、创设情境,引入新课。教师出示课件。(乱砍滥伐破坏环境的片段)师:同学们,看到这些你们有什么想说的吗?预设 生1:我想大声地呼吁:请不要再乱砍滥伐树木了,不然动物就无家可归了!生2:请保护我们共同的家园吧!生3:要保护我们的家园,就要大量植树。二、点明课题。师:说得太好了。要保护我们的家园,就要植树造林。还记得上节课我们学习中遇到的植树问题吗?今天这节课看看植树问题中还蕴含着哪些数学知识?(板书课题:乘法分配律)通过课件演示,创设情境,自然引发学生对保护环境的紧迫性,渗透环保教育。同时结合上节课的植树问题,更容易引起学生的注意和兴趣。方法二复习:在○里填上“<”“>”或“=”。①(3+2)×4○3×4+2×4② 2×(11+9)○2×11+2×9③(20+4)×5○20×5+4×5(学生独立完成)师:这三组算式老师不用计算,就可以判定用等号连接,这是为什么呢?难道这里有什么奥秘吗?今天,我们就一同来研究这个问题。(板书课题:乘法分配律)通过复习的形式,让学生先初步感知乘法分配律,然后经过老师的谈话,这三组算式老师不用计算,就可以判定用等号连接,这是为什么呢?给学生提出来一个疑问,激发学生对本节课探究的欲望。教学例7,掌握运用乘法分配律使运算变得简单。1.探究乘法运算定律。(课件出示例7)(1)寻找数学信息。师:仔细观察,你能得到哪些数学信息?预设 生1:一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。生2:每组要种5棵树,每棵树要浇2桶水。(2)提出数学问题。师:根据这些数学信息,你能提出什么问题?预设 生:一共有多少名同学参加了这次植树活动?(教师板书学生提出的数学问题)(3)独立列式计算。师:你用什么方法算出一共有多少名同学参加了这次植树活动?(学生独立计算)(4)交流解决问题的方法。(分小组讨论,用多种方法去解,比一比,谁算得快?每位同学把自己的想法、做法说给你的同桌听,教师巡视,参与小组讨论)(5)学生汇报。预设 生:我先算出每一组植树的人数,再乘25就是一共植树的人数。即: (4+2)×25 =6×25 =150(人)师:你为什么要将(4+2)打上括号呢?预设 生1:只有打括号才能先算。(教师肯定,大家鼓掌鼓励)生2:我分别算出25个小组挖坑、种树的人数和25个小组抬水、浇树的人数,加在一起就是一共植树的人数,即: 4×25+2×25 =100+50 =150(人)师:同学们,你们同意他的做法吗?预设 生:同意。师:将生1、生2的两种做法板书在黑板上。 (4+2)×25 4×25+2×25 =6×25 =100+50 =150(人) =150(人)让学生自己寻找数学信息,提出问题,并且独立解决问题。促成多种解决问题方法的生成,为探究运算定律准备了资源。在交流解决问题的方法时,突出解决问题的步骤,使学生了解每种方法的思路的同时,领悟算式之间的相等关系。2.探究乘法分配律。(1)再次验证。师:真奇怪,两个不同的算式,得数怎么相同啊!大家再检查一下他们做得对吗?预设 生:对。(2)小组讨论,探究规律。师:你们发现什么规律了吗?(分小组讨论)预设 生:我发现(4+2)×25=4×25+2×25。师:为什么?预设 生:因为它们的结果相同,所以算式就相等。师:你们同意他的说法吗?预设 生:同意。师:你们还发现了什么?预设 生:我发现根据左边的算式能推出右边的算式,即:(4+2)×25=4×25+2×25。(教师让学生到黑板前给大家演示)师:你们同意他的说法吗?预设 生:同意。(3)变式训练,验证规律。师:假如是25×(4+2)=,你能推出等号右边的算式吗?(凝视片刻,有同学举手,还有私下说出做法的)预设 生:25×(4+2)=25×4+25×2。师:你们同意他的说法吗?预设 生:同意。师:举例(3+4)×26, 43×(10+5)。你们能推出右边的算式吗?(提问两个同学到黑板前来做,其他同学在练习本上做)师:你能给你的同桌出两道这样的题吗?(学生出题,同桌互算)(4)交流概括,符号表示。师:你能用符号或字母写出这个规律吗?板书:(a+b)×c= × + × a×(b+c)= × + × (提问学生到黑板前做,其他同学在本子上做)师:你能用语言叙述这个规律吗?(分小组或同桌互相叙述)预设 生:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。(教师板书)放手让学生自主探究规律,发现和总结乘法分配律,完全符合学生的认知能力和已有的知识基础,更能帮助学生进一步理解掌握乘法分配律。3.探讨各运算定律之间的区别。师:想一想,我们已经探讨、发现了几条乘法运算定律?预设 生:3条。分别是乘法交换律和乘法结合律,还有今天学习的乘法分配律。师:我们发现了3条乘法运算定律和2条加法运算定律。请同学们比较加法的交换律、结合律,乘法的交换律、结合律和乘法分配律,你发现它们之间有什么区别吗?(小组讨论)师:哪一个小组汇报一下讨论结果?预设 生1:我们认为加法的两条定律是加法运算的规律,乘法交换律和乘法结合律是乘法运算的规律。乘法分配律是乘法和加法总运算之间的规律。生2:我们讨论的和他们组差不多,简单点说就是这五条运算定律,只有乘法分配律是两种运算之间的规律。师:通过讨论,大家都清楚了乘法的交换律、结合律和加法的交换律、结合律是同一种运算的规律。乘法分配律是乘、加两种运算之间的规律。乘法分配律在运算中具有特殊的意义。请学生讨论所学五条运算定律的区别,给学生提供回顾整理所学运算定律的空间。讨论交流活动,使学生加深对乘法分配律的认识,也促使学生形成更好的认知结构。练习11.教材第26页“做一做”第1,2题。2.课本第27页练习七第4题。学生独立完成练习题,完成后组织学生集体讨论订正。【参考答案】 做一做:1.✕ ✕ √ 2.乘法分配律练习七:4.117×3+117×7=117×(3+7)4×a+a×5=(4+5)×a 以上两个算式应用了乘法分配律师:这节课你们学了什么知识?有什么收获?预设 生1:我学会了乘法分配律,两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。生2:我会用字母表示乘法分配律:(a+b)×c=a×c+b×c。生3:我知道乘法的交换律、结合律和加法的交换律、结合律是同一种运算的规律,乘法分配律是乘、加两种运算之间的规律。作业1教材第28页练习七第6,8题。乘法分配律25×(4+2)=25×4+25×2两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。(a+b)×c=a×c+b×ca×(b+c)=a×b+a×c1.从学生已有生活经验出发,通过观察、类比、归纳、验证等方法深化和丰富对乘法分配律的认识。2.渗透“由特殊到一般,再由一般到特殊”的认识事物的方法,培养学生独立自主、主动探索、发现问题、解决问题的能力,提高数学的应用意识。3.注重从实际出发,把数学知识和实际生活紧密联系起来,让学生在体验中学到知识。1.在要求同学们去总结乘法分配律的概念时老师没有很好地引导,导致学生对乘法分配律特点的认识比较模糊。2.在学生总结出乘法分配律的概念时,只是一笔带过地把乘法分配律通过课件展示给学生们看了一遍,没有反复强调乘法分配律的特点,导致个别学生没有较好地掌握乘法分配律,把乘法分配律和乘法结合律弄混。再次教学中,对于概念的教学要引导好,多让学生说一说,表达自己的想法,帮助学生理解好概念,同时强调乘法分配律的特点,让学生能对乘法分配律有选择地使用。 水果店运来梨和苹果各25筐,每筐苹果重40千克,每筐梨重30千克,水果店运来梨和苹果共多少千克?[名师点拨] 此题可以先求出梨和苹果各重多少千克,之后再加在一起,即25×40+25×30;也可以先求出一筐梨和一筐苹果的质量,再求出25筐苹果和25筐梨一共重多少千克,即25×(40+30)。[解答] 方法一: 25×40+25×30 =1000+750 =1750(千克)方法二: 25×(40+30) =25×70 =1750(千克)答:水果店运来梨和苹果共1750千克。【知识拓展】 在运用乘法分配律进行计算时,要熟记字母表达式,乘法分配律不仅可以用在乘、加这两种运算中,也可以用在乘、减中,但要注意运算符号。警察抓小偷传说中有两个狡猾的小偷,暂且称他们为65和35吧,他俩凭借小聪明盗取钱财无数。为此,警局特派警察16专门负责缉捕,聪明机智的警察16很快就顺利抓获他们,将他们“请”进了监狱,为防其逃跑,警察16专门看守他们。(65×16+35×16=(65+35)×16)两个小偷追悔莫及。当他们的家人来探监的时候,他俩痛哭流涕。世上没有后悔药,他们成了犯人,警察当然得一一跟着他们,监视他们探监。((65+35)×16=65×16+35×16)像16这样的好警察屡见不鲜。当然,并不是所有的小偷都能顺利抓获,他们有的很会使用“障眼法”。你看79×21+21,警察21要抓两个小偷,可找来找去只逮到一个小偷79,还有一个在哪里呢?原来,他就躲在警察的眼皮底下呢(即21为21×1),难怪不好找!邪不胜正,智慧英明的警察还是抓住了他,把他们关起来并看守(21×(79+1))。再看102×15,警察15要抓小偷,可根本找不着小偷,你们知道小偷怎么伪装的吗?原来他们经过乔装打扮成了102,其实那是两个小偷100和2,你看2不躲在100的背后嘛!同学们,故事有趣吗?你们掌握乘法分配律了吗?乘法分配律知识拓展乘法分配律特别要注意“两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加”中的“分别”两个字。 类型一:(注意:一定要括号外的数分别乘括号里的两个数,再把积相加) 例: (40+8)×25 =40×25+8×25 =1000+200 =1200类型二:(注意:两个积中相同的因数只能写一次) 例: 75×23+25×23 =23×(75+25) =23×100 =2300类型三:(提示:把102看作100+2;81看作80+1,再用乘法分配律) 例: 78×102 =78×(100+2) =78×100+78×2 =7800+156 =7956例: 125×81 =125×(80+1) =125×80+125×1 =10000+125 =10125类型四:(提示:把99看作100-1;39看作40-1,再用乘法分配律) 例: 31×99 =31×(100-1) =31×100-31×1 =3100-31 =3069例: 25×39 =25×(40-1) =25×40-25×1 =1000-25 =975类型五:(提示:把83看作83×1,再用乘法分配律) 例: 83+83×99 =83×1+83×99 =83×(1+99) =83×100 =8300