高中数学北师大版 (2019)选择性必修 第一册1.1 直线拟合教课ppt课件

这是一份高中数学北师大版 (2019)选择性必修 第一册1.1 直线拟合教课ppt课件
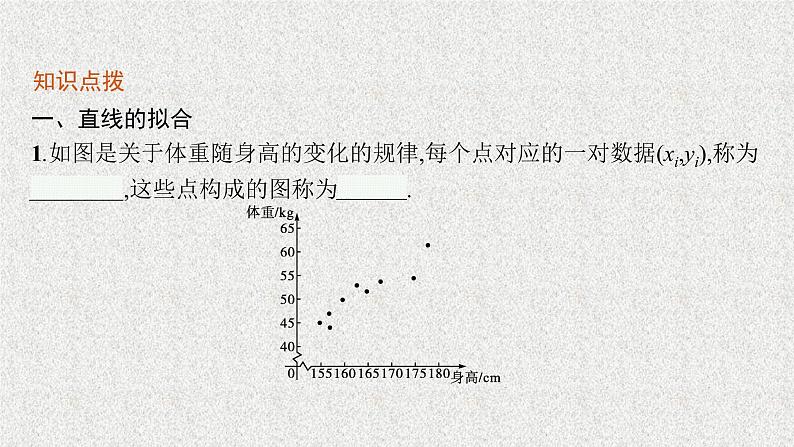
第七章2021内容索引课前篇 自主预习课堂篇 探究学习课前篇 自主预习激趣诱思知识点拨一、直线的拟合1.如图是关于体重随身高的变化的规律,每个点对应的一对数据(xi,yi),称为成对数据,这些点构成的图称为散点图.2.从散点图上可以看出,如果变量之间存在着某种关系,这些点会有一个大致趋势,这种趋势通常可以用一条光滑的曲线来近似地描述.这样近似描述的过程称为曲线拟合.若在两个变量X和Y的散点图中,所有点看上去都在一条直线附近波动,此时就可以用一条直线来近似地描述这两个量之间的关系,称之为直线拟合.名师点析1.相关关系:两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.2.正相关与负相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关;如果当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.微练习下列两个变量具有相关关系的是(　　)A.角度和它的余弦值B.正方形的边长和面积C.直线上的点与该点的坐标D.人的身高和体重答案 D解析 A,B,C具有确定性的函数关系;一般地,身高越高,体重越重,是相关关系.故选D微思考相关关系与函数关系有什么异同点?提示相同点:两者均是指两个变量的关系.不同点:①函数关系是一种确定的关系,如圆的面积S与半径r的关系,它可以用函数关系式S=πr2来表示;相关关系是一种非确定的关系,如人的体重y与身高x有关,一般来说,身高越高,体重越重,但不能用一个函数关系式来严格地表示它们之间的关系.②函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.二、一元线性回归方程1.最小二乘法对于给定的两个变量X和Y(如身高和体重),可以把其成对的观测值(x1,y1),(x2,y2),…,(xn,yn)表示为平面直角坐标系中的n个点.现在希望找到一条直线Y=a+bX,使得对每一个xi(i=1,2,…,n),由这个直线方程计算出来的值a+bxi与实际观测值yi的差异尽可能小.为此,希望[y1-(a+bx1)]2+[y2-(a+bx2)]2+…+[yn-(a+bxn)]2达到最小.换句话说,我们希望a,b的取值能使上式达到最小.这个方法称为最小二乘法.2.线性回归方程的系数的计算公式 名师点析1.线性回归系数的求解公式还可以写成如下形式: 2.在回归分析中,利用线性回归方程求出的值不一定是真实值,很多时候只是预测值.例如,人的体重与身高存在一定的线性相关关系,但体重除了受身高的影响外,还受其他因素的影响,如饮食习惯、是否喜欢运动等.微练习如果记录了X,Y的几组数据分别为(0,1),(1,3),(2,5),(3,7),那么Y关于X的回归直线必过点(　　)A.(2,2)B.(1.5,2)C.(1,2)D.(1.5,4)答案 D 课堂篇 探究学习例1下面4个散点图中,不适合用直线拟合其中两个变量的是(　　) 答案 A解析 根据题意知,适合用直线拟合其中两个变量的散点图,必须是散点分布比较集中,且大体接近于某一条直线,分析选项中的4个散点图可得,A中的散点杂乱无章,最不符合条件.反思感悟 一般地,直观地判断线性相关性就是观察散点图是否近似成一条直线,等学习了后续的相关系数,还可以理论上进行判断.变式训练1如图四个散点图中,适合用直线拟合其中两个变量的是(　　) A.①② B.①③ C.②③ D.③④ 答案 B解析 根据题意,适合用直线拟合其中两个变量的散点图,必须是散点分布比较集中,且大体接近某一条直线的,分析4个散点图可得①③符合条件.例2一车间为规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,测得的数据如下,根据下表可得线性回归方程Y=8X+11,则实数a的值为(　　)A.34 B.35 C.36 D.37 答案 C 延伸探究将例2改为如下:一车间为规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,测得的数据如下,根据下表可得线性回归方答案 8 例3若从某大学中随机选取8名女大学生,其身高和体重数据如表所示:求根据女大学生的身高预测体重的线性回归方程,并预测一名身高为172 cm的女大学生的体重.解 (1)画散点图选取身高为横坐标,体重为纵坐标,画出散点图,展示两个变量之间的关系,并判断二者是否具有线性关系.于是得到线性回归方程为Y=0.848X-85.712.(3)预测和决策当X=172时,Y=0.848×172-85.712=60.144(kg),即一名身高为172 cm的女大学生的体重预测值为60.144 kg.反思感悟 在使用线性回归方程进行预测时要注意:(1)线性回归方程只适用于我们所研究的样本的总体.(2)我们所建立的线性回归方程一般都有时间性.(3)样本取值的范围会影响线性回归方程的适用范围.(4)不能期望线性回归方程得到的预测值就是精确值.变式训练2PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某时间段车流量与PM2.5浓度的数据如下表:(1)根据上表数据,用最小二乘法求出Y关于X的线性回归方程;(2)若周六同一时段车流量是200万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度.故Y关于X的线性回归方程为Y=0.72X+6.24.(2)当X=200时,Y=0.72×200+6.24=150.24(微克/立方米).所以可以预测此时PM2.5的浓度为150.24微克/立方米.方法优化——求线性回归方程的技巧典例某地粮食需求量逐年上升,部分统计数据如下表:(1)利用所给数据求年需求量Y关于年份X的线性回归方程;(2)利用(1)中所求出的线性回归方程预测该地2021年的粮食需求量.解 (1)由所给数据看出,年需求量与年份之间具有线性相关关系.下面来求线性回归方程,先将数据处理如下: 由上述计算结果,可知所求线性回归方程为Y-257=6.5(X-2 015)+3.2,即Y=6.5(X-2 015)+260.2.(2)利用所求得的线性回归方程,可预测2021年的粮食需求量为6.5×(2 021-2 015)+260.2=6.5×6+260.2=299.2(万吨).方法点睛求线性回归方程时,重点考查的是计算能力.若本题用一般方法去解,则计算比较烦琐(如年份、需求量不做如上处理),所以平时训练时遇到数据较大时要考虑有没有更简便的方法解决.变式训练某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,根据试验数据得到如图所示的散点图,其中X表示零件的个数,Y表示加工时间,则Y关于X的线性回归方程是　　　　　. 答案 Y=0.7X+1.05 所以线性回归方程为Y=0.7X+1.05. 1.已知变量X,Y之间具有线性相关关系,其散点图如图所示,则其线性回归方程可能为(　　)A.y=1.5x+2 B.y=-1.5x-2C.y=1.5x-2 D.y=-1.5x+2答案 D解析 由散点图知变量X,Y之间负相关,排除A,C,当X=0时,Y>0,排除B,故有可能是D.A.1.5 B.1.8 C.2 D.1.6 答案 D 3.如图为制作某款木制品的过程中,产量X吨与相应的消耗木材Y吨的统计数据,经计算得到Y关于X的线性回归方程Y=0.7X+0.85,由于某些原因m处的数据看不清楚了,则根据运算可得m=　　　　. 答案 5.5 解得m=5.5. 4.(2021陕西西安模拟)某商店在2020年上半年前5个月的销售额如表所示: (1)若从这5个月中随机选取1个月计算销售纯收入,求选取月份的销售额不低于2万元的概率;(2)求销售额Y(单位:千元)关于月份X的线性回归方程,并预测该商店2020年上半年的销售总额.解 (1)因为这5个月中销售额不低于2万元的只有4月和5月,所以所求概率故销售额Y关于月份X的线性回归方程为Y=4.3X+4.1.当X=6时,Y=4.3×6+4.1=29.9(千元).故该商店2020年上半年的销售总额为8+13+17+22+25+29.9=114.9(千元),即11.49万元.(注:单位写千元或万元都可以)本 课 结 束