高中数学北师大版 (2019)选择性必修 第一册3.2 离散型随机变量的方差多媒体教学ppt课件

这是一份高中数学北师大版 (2019)选择性必修 第一册3.2 离散型随机变量的方差多媒体教学ppt课件
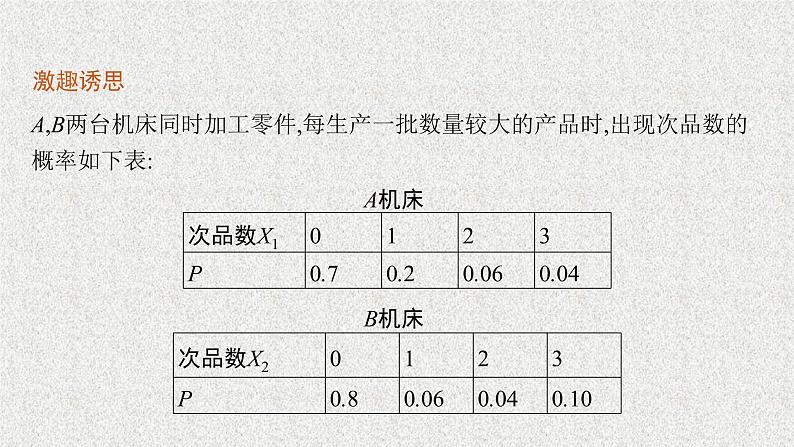
第六章2021内容索引课前篇 自主预习课堂篇 探究学习课前篇 自主预习激趣诱思A,B两台机床同时加工零件,每生产一批数量较大的产品时,出现次品数的概率如下表:A机床 B机床 在上述问题中,由EX1和EX2的值能比较两台机床的产品质量吗?为什么?试想利用什么指标可以比较A,B两台机床的加工质量?知识点拨一、离散型随机变量的方差、标准差若离散型随机变量X的分布列如下表则(xi-EX)2描述了xi(i=1,2,…,n)相对于均值EX的偏离程度,而DX=E(X-EX)2= (xi-EX)2pi为这些偏离程度的加权平均,刻画了随机变量X与其均值EX的平均偏离程度.我们称DX为随机变量X的方差,其算术平方根 为随机变量X的标准差,记作σX.随机变量的方差DX和标准差σX都反映了随机变量的取值偏离于均值的平均程度.方差(标准差)越小,则随机变量偏离于均值的平均程度越小;反之,方差(标准差)越大,则随机变量的取值越分散.微练习1下列说法正确的有　　　　.(填序号) ①离散型随机变量X的期望EX反映了X取值的概率的平均值;②离散型随机变量X的方差DX反映了X取值的平均水平;③离散型随机变量X的期望EX反映了X取值的波动水平;④离散型随机变量X的方差DX反映了X取值的波动水平.答案 ④解析 ①错误,因为离散型随机变量X的期望EX反映了X取值的平均水平.②错误,因为离散型随机变量X的方差DX反映了随机变量偏离于期望的平均程度.③错误,因为离散型随机变量的方差DX反映了X取值的波动水平,而随机变量的期望EX反映了X取值的平均水平.④正确,由方差的意义可知.微练习2已知随机变量X,DX= ,则X的标准差为　　　　. 二、方差的性质若X是随机变量,Y=aX+b也是随机变量,则DY=D(aX+b)=a2DX.名师点析微练习已知随机变量ξ的方差Dξ=4,且随机变量η=2ξ+5,则Dη=　　　　.答案 16 解析 由D(aξ+b)=a2Dξ,得Dη=D(2ξ+5)=22×Dξ=16. 课堂篇 探究学习例1袋中有20个大小相同的球,其中记为0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球,ξ表示所取球的标号,求ξ的分布列、均值和方差.故ξ的分布列为 延伸探究在本例条件下,若η=aξ+b,Eη=1,Dη=11,试求a,b的值. 解 由D(aξ+b)=a2Dξ=11,E(aξ+b)=aEξ+b=1,及Eξ=1.5,Dξ=2.75,得2.75a2=11,1.5a+b=1,解得a=2,b=-2或a=-2,b=4.反思感悟 (1)求离散型随机变量X的方差的步骤①理解X的意义,写出X的所有可能的取值;②求X取每一个值的概率;③写出随机变量X的分布列;④由均值、方差的定义求EX,DX.(2)对于变量间存在关系的方差,在求解过程中应注意方差性质的应用,如D(aξ+b)=a2Dξ,这样处理既避免了求随机变量η=aξ+b的分布列,又避免了繁杂的计算,简化了计算过程.变式训练1甲、乙两人进行定点投篮游戏,投篮者若投中,则继续投篮,否则由对方投篮,第一次由甲投篮;已知每次投篮甲、乙命中的概率分别为 在前3次投篮中,乙投篮的次数为ξ,求ξ的分布列、期望和方差.故ξ的分布列为 例2甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所得次品数分别为ξ,η,ξ和η的分布列如下:试对这两名工人的技术水平进行比较. 由Eξ=Eη知,两人出次品的平均数相同,技术水平相当,但Dξ>Dη,可见乙的技术比较稳定.反思感悟 均值仅体现了随机变量取值的平均大小,而方差则说明了随机变量取值的稳定程度.因此,我们可以利用均值和方差的意义分析、解决实际问题.当我们希望实际的平均水平比较理想时,不但要比较它们的均值,还应看它们相对于均值的偏离程度;如果我们希望比较稳定时,应先考虑方差,再考虑均值是否接近.变式训练2有甲、乙两名学生,经统计,他们在解答同一份数学试卷时,各自的成绩在80分、90分、100分的概率分布大致如下表所示:甲 乙试分析两名学生的成绩水平. 解 甲同学成绩的期望与方差分别为EX=80×0.2+90×0.6+100×0.2=90,DX=(80-90)2×0.2+(90-90)2×0.6+(100-90)2×0.2=40.乙同学成绩的期望与方差分别为EY=80×0.4+90×0.2+100×0.4=90,DY=(80-90)2×0.4+(90-90)2×0.2+(100-90)2×0.4=80,所以甲同学成绩稳定,乙同学成绩波动大.随机变量的方差与高考典例1(2020全国3,理3)在一组样本数据中,1,2,3,4出现的频率分别为 A.p1=p4=0.1,p2=p3=0.4B.p1=p4=0.4,p2=p3=0.1C.p1=p4=0.2,p2=p3=0.3D.p1=p4=0.3,p2=p3=0.2解析 四个选项的数据都具有对称性,平均数均为2.5,其中B选项的数据中,极端值最多,数据波动程度最大,故选B.答案 B典例2(2019浙江,7)设0