初中数学湘教版七年级下册4.6 两条平行线间的距离习题课件ppt

这是一份初中数学湘教版七年级下册4.6 两条平行线间的距离习题课件ppt
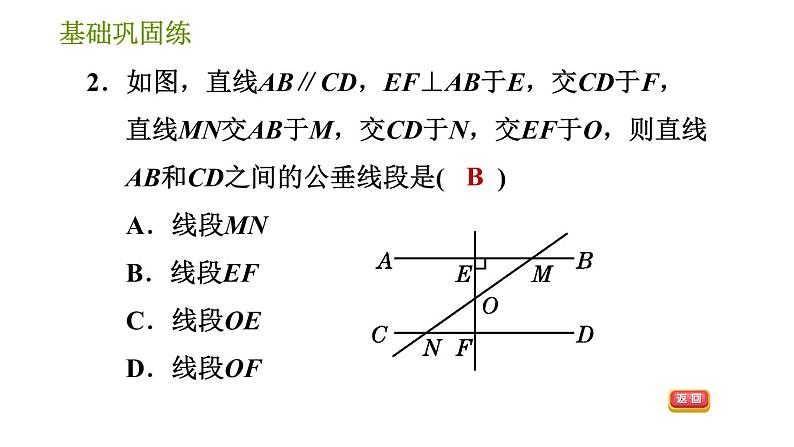
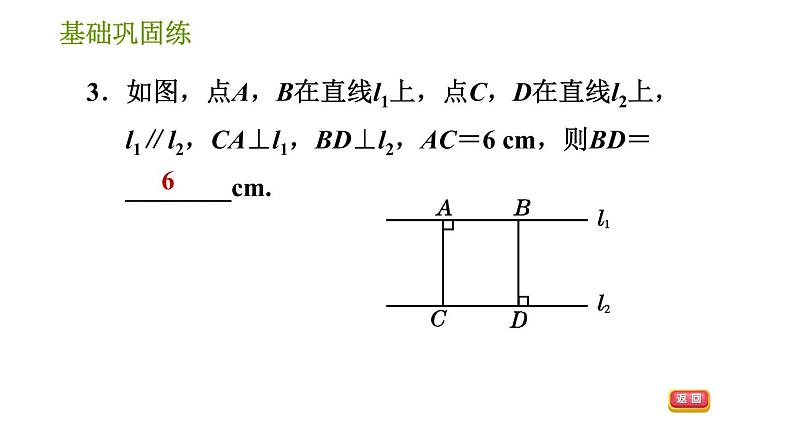
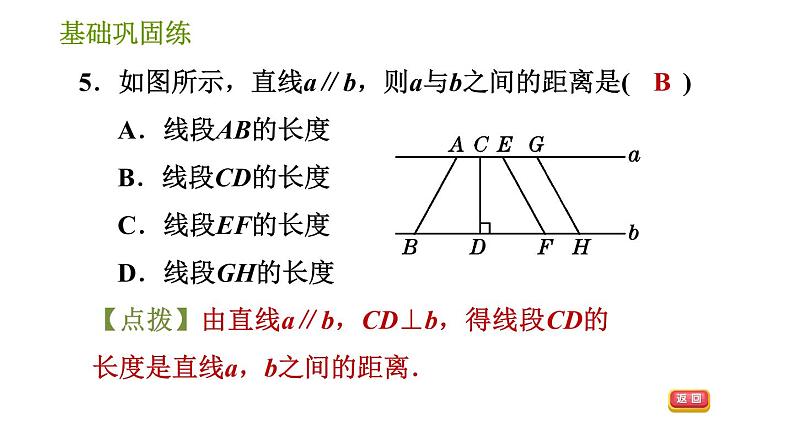
4.6　两条平行线间的距离第4章　相交线与平行线见习题见习题　见习题见习题CBBA7 cm或17 cm两条平行线的所有公垂线段都相等B见习题DB6垂直；垂足相等新知笔记答案显示长度1．与两条平行直线都________的直线，叫做这两条平行直线的公垂线，这时连接两个________的线段叫做这两条平行直线的公垂线段．2．两条平行线的所有公垂线段都________．3．两条平行线的公垂线段的________叫做两条平行线间的距离．垂直垂足相等长度1．两条平行线的公垂线段有(　　)A．1条 B．2条 C．3条 D．无数条D2．如图，直线AB∥CD，EF⊥AB于E，交CD于F，直线MN交AB于M，交CD于N，交EF于O，则直线AB和CD之间的公垂线段是(　　)A．线段MN B．线段EF C．线段OE D．线段OFB3．如图，点A，B在直线l1上，点C，D在直线l2上，l1∥l2，CA⊥l1，BD⊥l2，AC＝6 cm，则BD＝________cm.64. (荣德原创)甲、乙两名同学按照如图方式测量了数学课本不同位置的宽度，发现得到的宽度相等，理由：______________________________________．两条平行线的所有公垂线段都相等5．如图所示，直线a∥b，则a与b之间的距离是(　　)A．线段AB的长度 B．线段CD的长度C．线段EF的长度 D．线段GH的长度【点拨】由直线a∥b，CD⊥b，得线段CD的长度是直线a，b之间的距离．B6．平行线之间的距离是指(　　)A．从一条直线上一点到另一条直线的垂线段B．从一条直线上一点到另一条直线的垂线段的长度C．从一条直线上一点到另一条直线的垂线的长度D．从一条直线上一点到另一条直线上的一点间线段的长度B7．【教材改编题】如图，已知直线a∥b∥c，直线d与它们分别垂直且相交于A，B，C三点，若AB＝3，AC＝8，则平行线b，c之间的距离是(　　)A．3 B．5 C．8 D．11【点拨】因为直线a∥b∥c，直线d与它们分别垂直且相交于A，B，C三点，所以AB长为直线a和b之间的距离，BC长为直线b和c之间的距离，AC长为直线a和c之间的距离，又因为AB＝3，AC＝8，所以BC＝8－3＝5，即直线b与直线c之间的距离为5.【答案】B　8．如图，AD∥BC，AC与BD相交于点O，若S三角形ABD＝10，则S三角形ACD＝(　　)A．10 B．9 C．8 D．7A【点拨】因为AD∥BC，所以三角形ABD和三角形ACD的AD边上的高相等，即三角形ABD和三角形ACD同底等高，所以S三角形ACD＝S三角形ABD＝10.9.【2021·合肥蜀山区期末】如图，直线l1与l2相交于点O，点P是平面内任意一点，若点P到直线l1的距离为2，到直线l2的距离为3，则符合条件的点P有(　　)A．2个 B．3个C．4个 D．无数个【答案】C10．【中考·铜仁】设AB，CD，EF是同一平面内三条互相平行的直线，已知AB与CD的距离是12 cm，EF与CD的距离是5 cm，则AB与EF的距离等于____________．【点拨】分两种情况：①当EF在AB，CD之间时， 因为AB与CD的距离是12 cm，EF与CD的距离是5 cm，所以EF与AB的距离为12－5＝7(cm)．②当EF在AB，CD同侧时，因为AB与CD的距离是12 cm，EF与CD的距离是5 cm，所以EF与AB的距离为12＋5＝17(cm)．综上所述，EF与AB的距离为7 cm或17 cm.【答案】7 cm或17 cm　11．如图，地面上一样高的电线杆AB，CD与地面垂直，小明想知道两根电线杆顶端A，C间的距离，他借来梯子与长绳子，将绳子一端系在电线杆AB的顶端A处，拉直绳子到电线杆CD的顶端C处，然后量出拉直后的绳子的长度．你认为他这样方便吗？怎样测量比较方便？说明理由．解：不方便．直接测量两根电线杆底端B，D间的距离比较方便，理由如下：因为电线杆AB，CD与地面垂直，所以AB∥CD，所以B，D间的距离等于A，C间的距离(两条平行线的所有公垂线段都相等)．12. (易错题)甲、乙两名同学分别在两条自西向东的平行跑道(AB，CD)上练习短跑，如图，两条跑道的间隔为2 m，发令时，乙在甲前方10 m处，若甲的速度为8.5 m/s；乙的速度为7.5 m/s.两人同时起跑，多少秒后，两人间的距离最小？最小距离为多少？【点拨】本题易因对两平行线间的距离不理解，忽略了甲、乙两位同学在不同的两条平行跑道上，误将最小距离当作0 m.解：当甲、乙两人所在位置的连线垂直于跑道时，两人间的距离最小，设t秒后两人间的距离最小，依题意得(8.5－7.5)t＝10.解得t＝10.所以两人同时起跑，10 s后，两人间的距离最小，最小距离为2 m.13．【中考·六盘水】如图，已知l1∥l2，C1在l1上，并且C1A⊥l2，A为垂足，C2，C3是l1上任意两点，点B在l2上．设三角形ABC1的面积为S1，三角形ABC2的面积为S2，三角形ABC3的面积为S3，小颖认为S1＝S2＝S3，请帮小颖说明理由．解：因为直线l1∥l2，所以三角形ABC1，三角形ABC2，三角形ABC3的底边AB上的高相等，所以三角形ABC1，三角形ABC2，三角形ABC3这3个三角形同底等高，所以三角形ABC1，三角形ABC2，三角形ABC3这3个三角形的面积相等，即S1＝S2＝S3.14．如图，四边形ABCD放在了一组距离相等的平行线中，已知BD＝6，四边形ABCD的面积为24，求相邻两条平行线间的距离．15．我们把能平分四边形面积的直线称为“好线”．利用下面的作图方法，可以得到四边形的“好线”：如图①，在四边形ABCD中，取对角线BD的中点O，连接OA，OC.显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，连接AE，则直线AE即为一条“好线”．(1)试说明直线AE是“好线”；解：因为OE∥AC，所以S三角形AOC＝S三角形AEC.又因为折线AOC能平分四边形ABCD的面积，所以直线AE平分四边形ABCD的面积，即AE是“好线”．(2)如图②，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，并对作图进行适当说明(不需要说明理由)；B(3)解决上述问题时，没有用到的几何性质或数学思想是(　　)A．两平行线间的距离处处相等B．从特殊到一般的思想C．等(同)底等(同)高的两个三角形面积相等D．转化思想