

2021-2022学年河南省南阳市第一中学校高一上学期第二次月考数学试题含解析
展开河南省南阳市第一中学校2021-2022学年高一上学期第二次月考
数学试题
| 一、单选题 |
1.设全集,,,则( )
A. B. C. D.
【答案】B
【分析】
利用补集和交集的定义可求得集合.
【详解】
由已知可得,因此,.
故选:B.
2.命题“,”的否定是( )
A., B.,
C., D.,
【答案】C
【分析】
利用全称命题的否定可得出结论.
【详解】
由全称命题的否定可知,命题“,”的否定是“,”.
故选:C.
3.设集合M={x|x>2},P={x|x<6},那么“x∈M或x∈P”是“x∈M∩P”的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
【答案】C
【分析】
“x∈M或x∈P”即x∈M∪P,再利用x∈M∩P与x∈M∪P之间的关系即可判断出结论.
【详解】
“x∈M或x∈P”即x∈M∪P,M∪P={x|x>2}∪{x|x<6}=R,M∩P={x|2<x<6}.
∴x∈M∩P⇒x∈M∪P,反之不成立.
∴“x∈M或x∈P”是“x∈M∩P”的必要不充分条件.
故选:C.
4.设函数,则的表达式为( )
A. B.
C. D.
【答案】B
【分析】
令,则可得,然后可得答案.
【详解】
令,则可得
所以,所以
故选:B
【点睛】
易错点睛:本题主要考查函数解析式的求法,主要涉及了用换元法,要注意换元后的取值范围,考查学生的转化与化归能力,属于基础题.
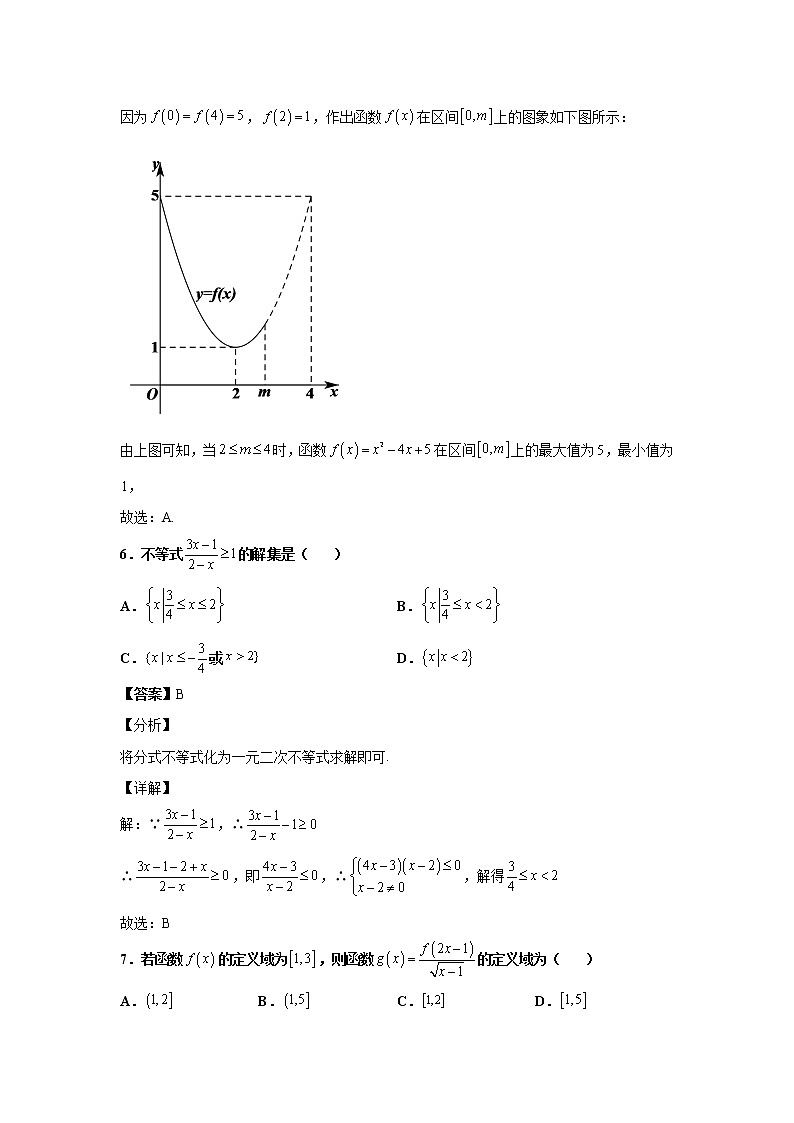
5.函数在区间上的最大值为,最小值为,则实数的取值范围是( )
A. B. C. D.
【答案】A
【分析】
求得,,作出函数在区间上的图象,数形结合可得出实数的取值范围.
【详解】
因为,,作出函数在区间上的图象如下图所示:
由上图可知,当时,函数在区间上的最大值为,最小值为,
故选:A.
6.不等式的解集是( )
A. B.
C.或 D.
【答案】B
【分析】
将分式不等式化为一元二次不等式求解即可.
【详解】
解:∵,∴
∴,即,∴,解得
故选:B
7.若函数的定义域为,则函数的定义域为( )
A. B. C. D.
【答案】A
【分析】
利用复合函数的定义及给定函数式列出不等式组,求出其解集即可作答.
【详解】
因函数的定义域为,则在函数中,
必有,解得,
所以的定义域为.
故选:A
8.函数的图象大致为( )
A. B.
C. D.
【答案】D
【分析】
根据函数的奇偶性可排除选项A,B;根据函数在上的单调性可排除选项C,进而可得正确选项.
【详解】
函数的定义域为且,关于原点对称,
因为,
所以是偶函数,图象关于轴对称,故排除选项A,B,
当时,,
由在上单调递增,在上单调递减,
可得在上单调递增,排除选项C,
故选:D.
9.已知函数在上单调递减,则实数的取值范围是( )
A.,, B.
C.,, D.,,
【答案】C
【分析】
先用分离常数法得到,由单调性列不等式组,求出实数的取值范围.
【详解】
解:根据题意,函数,
若在区间上单调递减,必有,
解可得:或,即的取值范围为,,,
故选:C.
10.已知函数满足对任意,都有成立,则的取值范围是( )
A.(0,3) B.
C.(0,2] D.(0,2)
【答案】C
【分析】
根据对任意,都有成立,得到函数在R上是减函数求解.
【详解】
因为对任意,都有成立,
所以函数在R上是减函数,
所以 ,解得,
所以实数的取值范围是 (0,2].
故选:C
11.若实数,则的最小值为( )
A. B.1 C. D.2
【答案】D
【分析】
由条件变形,再结合基本不等式求最小值.
【详解】
由条件可知,,
所以
,
当,即,结合条件 ,
可知时,等号成立,所以的最小值为.
故选:D
12.设奇函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,则不等式≤0的解集为( )
A.(-∞,-2]∪(0,2] B.[-2,0)∪[2,+∞)
C.(-∞,-2]∪[2,+∞) D.[-2,0)∪(0,2]
【答案】D
【分析】
由给定条件可得函数f(x)在(0,2)上的函数值为正,在(2,+∞)上的函数值为负,利用奇函数的性质化简不等式,解出不等式即得.
【详解】
因函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,即函数f(x)在(0,2)上的函数值为正,在(2,+∞)上的函数值为负,
又f(x)是奇函数,于是得,
因此,当x>0时,,则有0<x≤2,当x<0时,f(x)≤0,由奇函数的性质得-2≤x<0,
综上,不等式≤0的解集为[-2,0)∪(0,2].
故选:D
| 二、填空题 |
13.函数的值域是__________
【答案】
【分析】
由根式内部的代数式大于等于0求出函数的定义域,再由函数的单调性求得答案.
【详解】
由,得,
又在上的增函数,在上也是增函数,
在上是增函数,
则
函数的值域为
故答案为:
14.关于x的不等式的解集中恰有两个整数,则实数a的取值范围是______.
【答案】
【分析】
不等式化为,讨论与1的大小解出不等式即可得出.
【详解】
关于x的不等式可化为,
当时,解得,要使解集中恰有两个整数,则,
当时,不等式化为,此时无解,
当时,解得,要使解集中恰有两个整数,则,
综上,实数a的取值范围是.
故答案为:.
15.已知定义在上的奇函数,当时,,则_____.
【答案】
【分析】
根据奇函数的定义域关于原点对称可得的值,再由奇函数的定义即可求解.
【详解】
因为是定义在上的奇函数,
可得,解得:,
又由当时,,
所以,
故答案为:.
16.函数在上为增函数,则的一个单调递减区间是_________.
【答案】
【分析】
由函数为上的增函数,可知偶函数在单调递减,而是向左平移一个单位后得到的,进而求解.
【详解】
函数为上的增函数,
偶函数在上单调递增,在单调递减,
而是向左平移一个单位后得到的,
单调递减区间是,
故答案为:.
| 三、解答题 |
17.已知集合,,若A是B的充分不必要条件,求的取值范围.
【答案】
【分析】
由题意得到,分和两种情况讨论,结合集合的包含关系,列出不等式组,即可求解.
【详解】
由题意知A是B的充分不必要条件,可得集合,
当时,,解得,此时满足题意;
当时,要使得,则满足,解得,
综上所述,实数的取值范围为.
18.已知函数是定义在上的奇函数,且.
(1)求函数的解析式;
(2)用函数单调性的定义证明:在上为单调递增函数.
【答案】(1);(2)证明见解析.
【分析】
(1)根据,求出的值,求出函数的解析式即可;
(2)根据函数的单调性的定义证明即可.
【详解】
(1)函数是定义在上的奇函数,则,即,解得:,故;
(2)任意,设,则,
∵,,,且,,
∴,即在上递增.
19.函数在闭区间上的最小值记为.
(1)试写出的函数表达式;
(2)求的最小值.
【答案】(1);(2).
【分析】
(1)结合的对称轴,对进行分类讨论,结合二次函数的性质求得的表达式.
(2)结合二次函数的性质求得的最小值.
【详解】
(1)f(x)=x2-4x-4=(x-2)2-8,对称轴为,
当t>2时,f(x)在[t,t+1]上是增函数,
∴g(t)=f(t)=t2-4t-4;
当t≤2≤t+1,即1≤t≤2时,g(t)=f(2)=-8;
当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数,
∴g(t)=f(t+1)=t2-2t-7.
从而.
(2)当时,,对称轴为,所以,
当时,.
当时,,对称轴,所以,
所以的最小值为.
20.已知幂函数(,)在区间上单调递减.
(1)求的解析式;
(2)当时,恒成立,求的取值范围.
【答案】(1);(2).
【分析】
(1)利用幂函数的定义及性质结合已知条件列式计算即得;
(2)构造函数,再求出函数在指定区间上的最小值即可得解.
【详解】
(1)因幂函数在区间上单调递减,所以,解得
又,,则,此时,,即,
所以的解析式是;
(2)由(1)得,于是得不等式在上恒成立,
令,由(当且仅当,即时等号成立),即,
所以实数的取值范围是.
21.近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入a(单位:万元)满足P=3-6,乙城市收益Q与投入a(单位:万元)满足Q=a+2,设甲城市的投入为x(单位:万元),两个城市的总收益为f(x)(单位:万元).
(1)当甲城市投资50万元时,求此时公司的总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
【答案】(1)43.5(万元);(2)甲城市投资72万元,乙城市投资48万元.
【分析】
(1)直接代入收益公式进行计算即可.
(2)由收益公式写出f(x)=-x+3+26,令t=,将函数转为关于t的二次函数求最值即可.
【详解】
(1)当x=50时,此时甲城市投资50万元,乙城市投资70万元,所以公司的总收益为
3-6+×70+2=43.5(万元).
(2)由题知,甲城市投资x万元,乙城市投资(120-x)万元,所以f(x)=3-6+(120-x)+2=-x+3+26,
依题意得解得40≤x≤80.
故f(x)=-x+3+26(40≤x≤80).
令t=,则t∈[2,4],
所以y=-t2+3t+26=-(t-6)2+44.
当t=6,即x=72万元时,y的最大值为44万元,所以当甲城市投资72万元,乙城市投资48万元时,总收益最大,且最大收益为44万元.
【点睛】
本题考查函数模型的应用,考查函数最值的求解,属于基础题.
22.已知函数的定义域为,且对任意 ,都有,且当时,恒成立.
(1)证明:函数是奇函数;
(2)在定义域上单调递减;
(3),求的取值范围.
【答案】(1)见解析;(2)见解析;(3)
【分析】
(1)令,得到,令,,得到即可证明;
(2)设,则,由条件得,再由条件可得,即可得证;
(3)利用函数的奇偶性与单调性化抽象不等式为具体不等式组,即可得到结果.
【详解】
(1)证明: ,
令,
,则.
令,,
,
即,而,
,
即函数是奇函数;
(2)设,则,
当时,恒成立,则,
,
函数是上的减函数;
(3)由,
可得,又函数是奇函数,
∴,
∵在定义域上单调递减
∴ ,解得,
∴,
解得,,
故的取值范围.
河南省南阳市第一中学校2023-2024学年高一上学期第二次月考数学试题: 这是一份河南省南阳市第一中学校2023-2024学年高一上学期第二次月考数学试题,共9页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河南省南阳市第一中学校高一上学期第二次月考数学试题(解析版): 这是一份2022-2023学年河南省南阳市第一中学校高一上学期第二次月考数学试题(解析版),共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年河南省南阳市第一中学校高一上学期第三次月考数学试题 含解析: 这是一份2021-2022学年河南省南阳市第一中学校高一上学期第三次月考数学试题 含解析,共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












