




2021学年第五章 统计与概率5.3 概率5.3.2 事件之间的关系与运算课文课件ppt
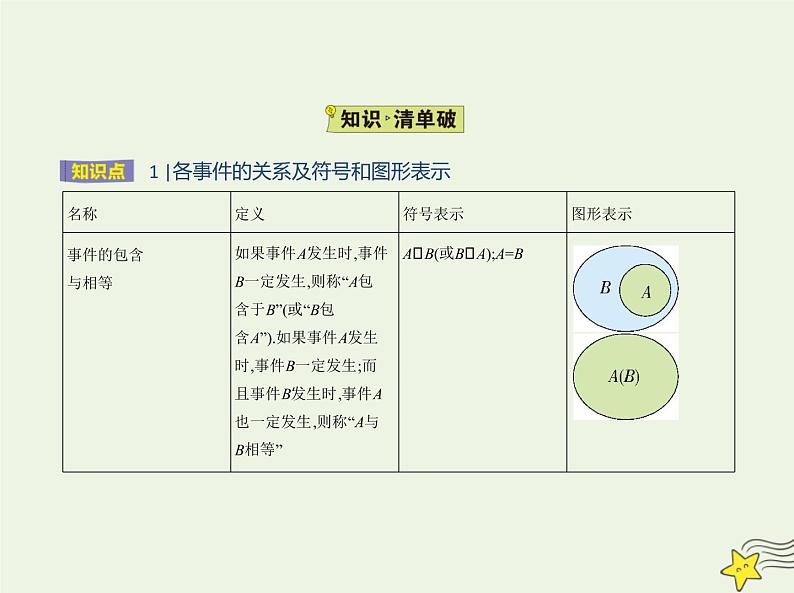
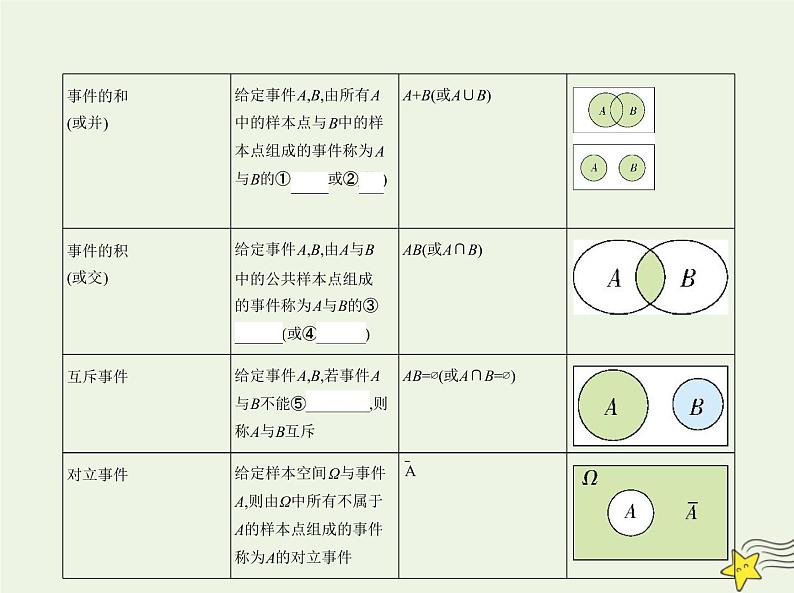
展开1 |各事件的关系及符号和图形表示
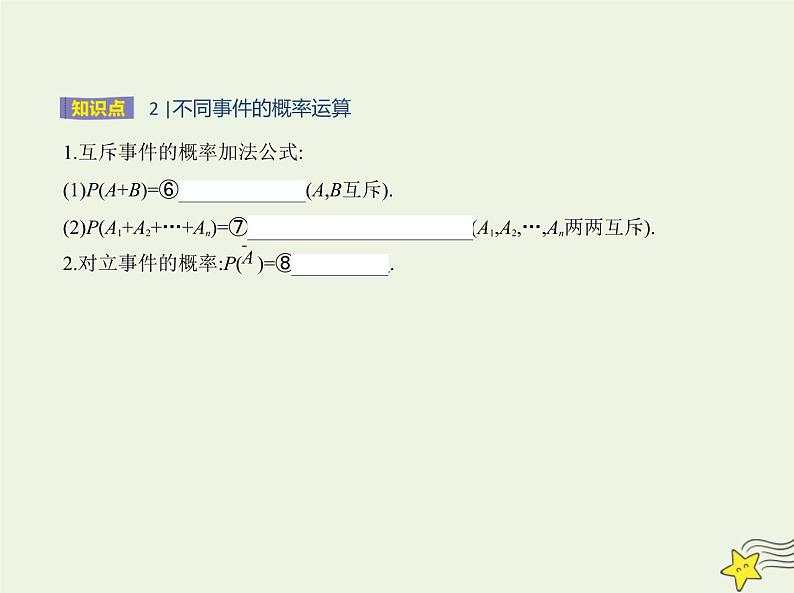
2 |不同事件的概率运算
1.互斥事件的概率加法公式:(1)P(A+B)=⑥ P(A)+P(B) (A,B互斥).(2)P(A1+A2+…+An)=⑦ P(A1)+P(A2)+…+P(An) (A1,A2,…,An两两互斥).
2.对立事件的概率:P( )=⑧ 1-P(A) .
判断正误,正确的画“ √” ,错误的画“ ✕” 。
1.互斥事件一定对立. ( ✕ )
2.对立事件一定互斥. ( √ )
3.事件A与B的和事件的概率一定大于事件A的概率. ( ✕ )
4.在一次随机试验中,彼此互斥的事件A,B,C,D满足A+B+C+D是必然事件,则A+C 与B+D是互斥事件,但不是对立事件. ( ✕ )
1 |互斥事件与对立事件
从2019年开始,山东省高考试点了选科走班,语文,数学,英语是高考必考科目,然后 从余下的物理,化学,生物,政治,地理,历史中选三科.
1.事件A:小白选化学与事件B:小白不选化学能同时发生吗?A与B合在一起是基本 事件吗?提示:不能.不是.
2.事件A:小白选化学与事件C:小白只从物理,生物,政治,地理,历史中选三科能同 时发生吗?它们的结果合在一起是样本空间吗?提示:不能.是.
1.对立事件是针对两个事件来说的.一般地,若两个事件对立,则这两个事件是互 斥事件;若两个事件是互斥事件,则这两个事件未必是对立事件,所以对立事件是 特殊的互斥事件,从充分必要条件的角度来讲,对立事件是互斥事件的充分不必 要条件.
2.若A,B为对立事件,则在一次试验中,事件A与B只能发生其中一个,并且必然发生 其中一个.
3.若事件A的对立事件记作 ,则P( )=1-P(A).这个公式为我们求P(A)提供了一种方法,当我们直接求P(A)的运算较复杂或有困 难时,可以转化为求P( ).
互斥事件和对立事件的判断方法:
1.判断两个事件是不是互斥事件,主要看它们在一次试验中能否同时发生,若不能 同时发生,则这两个事件是互斥事件,若能同时发生,则这两个事件不是互斥事件.
2.判断两个事件是不是对立事件,主要看在一次试验中这两个事件是否同时满足 两个条件:一是不能同时发生;二是必有一个发生.如果这两个条件同时成立,那么 这两个事件是对立事件,只要有一个条件不成立,这两个事件就不是对立事件.事实上,解决此类问题的关键是明晰“恰”“至少”“至多”“都”等关键词.
1.(★★☆)在学校的元旦文艺晚会上,某班的学生为了增加舞台效果,把红、黄、 黑、白4件不同颜色的衣服随机地分给甲、乙、丙、丁4个人,且每个人必须穿其 中的一件衣服,事件“甲穿黄衣”与“乙穿黄衣”是 ( C )A.对立事件B.不可能事件C.互斥但不对立事件D.以上均不对思路点拨:根据互斥事件及对立事件的定义判断.
解析 事件“甲穿黄衣”与“乙穿黄衣”是不能同时发生的两个事件,这两个事 件可能恰有一个发生,一个不发生,也有可能两个都不发生,所以它们为互斥但不 对立事件,应选C.
2.(★★☆)某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,判断下 列每对事件是不是互斥事件,如果是,再判断它们是不是对立事件.(1)恰有1名男生与恰有2名男生;(2)至少有1名男生与全是男生;(3)至少有1名男生与全是女生;(4)至少有1名男生与至少有1名女生.思路点拨:根据对立事件和互斥事件的定义进行判断.
解析 判断两个事件是否互斥,就要考察它们是否能同时发生;判断两个互斥事 件是否对立,就要考察它们是否必有一个发生.(1)因为“恰有1名男生”与“恰有2名男生”不可能同时发生,所以它们是互斥 事件;当恰有2名女生时它们都不发生,所以它们不是对立事件.(2)因为恰有2名男生时“至少有1名男生”与“全是男生”同时发生,所以它们 不是互斥事件.(3)因为“至少有1名男生”与“全是女生”不可能同时发生,所以它们互斥;由于 它们必有一个发生,所以它们是对立事件.(4)由于选出的是1名男生1名女生时“至少有1名男生”与“至少有1名女生”同 时发生,所以它们不是互斥事件.
方法总结 (1)包含关系、相等关系的判定:①事件的包含关系与集合的包含关系相似;②两事件相等的实质为相同事件,即同时发生或同时不发生.(2)判断事件是否互斥的两个步骤:第一步,确定每个事件包含的结果;第二步,确定是否有一个结果发生会意味着两个事件都发生,若是,则两个事件不 互斥,否则就是互斥的. (3)判断事件是否对立的两个步骤:第一步,判断是不是互斥事件;第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立.
2|事件及其表示的意义
1.事件及其表示的意义
2.事件的混合运算同数的加、减、乘、除混合运算一样,事件的混合运算也有优先级,我们规定:求 积运算的优先级高于求和运算,例如(A )+( B)可简写为A + B.
1.(★★☆)先后掷一个骰子两次,观察向上的点数,记事件A:点数之和等于6,事 件B:最大点数为4,事件C:点数都是偶数,说明下列各式的意义:A+B+C;AB .
解析 A+B+C表示A发生或B发生或C发生的和事件.AB 表示A、B同时发生且C不发生的积事件.
2.(★★☆)盒子里有6个红球,4个白球,现从中任取3个球,设事件A={3个球中有1个 红球,2个白球},事件B={3个球中有2个红球,1个白球},事件C={3个球中至少有1个 红球},事件D={3个球中既有红球又有白球}.问:(1)事件D与A,B是什么样的运算关系?(2)事件C与A的交事件是什么事件?(3)设事件E={3个球都是红球},事件F={3个球中至少有1个白球},那么事件C与A, B,E是什么运算关系?C与F的交事件是什么?思路点拨:根据事件及其表示的意义求解.
高中数学人教B版 (2019)必修 第二册5.3.2 事件之间的关系与运算评课课件ppt: 这是一份高中数学人教B版 (2019)必修 第二册5.3.2 事件之间的关系与运算评课课件ppt,共41页。PPT课件主要包含了目录索引等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第二册5.3.2 事件之间的关系与运算作业ppt课件: 这是一份高中数学人教B版 (2019)必修 第二册5.3.2 事件之间的关系与运算作业ppt课件,共19页。PPT课件主要包含了ABC等内容,欢迎下载使用。
2020-2021学年5.3.2 事件之间的关系与运算教课ppt课件: 这是一份2020-2021学年5.3.2 事件之间的关系与运算教课ppt课件,共36页。PPT课件主要包含了学习目标,一定发生,图5-3-2,和或并,图5-3-3,公共样本点,互斥事件,图5-3-4,对立事件,图5-3-5等内容,欢迎下载使用。













