
2019-2020学年广东省汕头市金平区七年级(上)期末数学试卷 解析版
展开2019-2020学年广东省汕头市金平区七年级(上)期末数学试卷
一、选择题(本题共10小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个是正确的,请将答题卡上对应的小题所选的选项涂黑.
1.(3分)3的相反数是( )
A. B. C.3 D.﹣3
2.(3分)过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )
A.3.12×105 B.3.12×106 C.31.2×105 D.0.312×107
3.(3分)把弯曲的河道改直,能够缩短航程,这样做的道理是( )
A.两点之间,射线最短 B.两点确定一条直线
C.两点之间,直线最短 D.两点之间,线段最短
4.(3分)下列各数中,在﹣2和0之间的数是( )
A.﹣1 B.1 C.﹣3 D.3
5.(3分)由五个小立方体搭成如图的几何体,从正面看到的平面图形是( )
A. B.
C. D.
6.(3分)下列方程中,解为x=2的是( )
A.2x=6 B.(x﹣3)(x+2)=0
C.x2=3 D.3x﹣6=0
7.(3分)下列运算中,正确的是( )
A.3a+2b=5ab B.3a2b﹣3ba2=0
C.2a3+3a2=5a5 D.5b2﹣4b2=1
8.(3分)如果a2﹣3b﹣1=0,那么多项式2a2﹣6b+2的值等于( )
A.1 B.4 C.﹣1 D.﹣4
9.(3分)一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.80% (1+50%)x=x﹣28 B.80% (1+50%)x=x+28
C.80% (1+50%x)=x﹣28 D.80% (1+50%x)=x+28
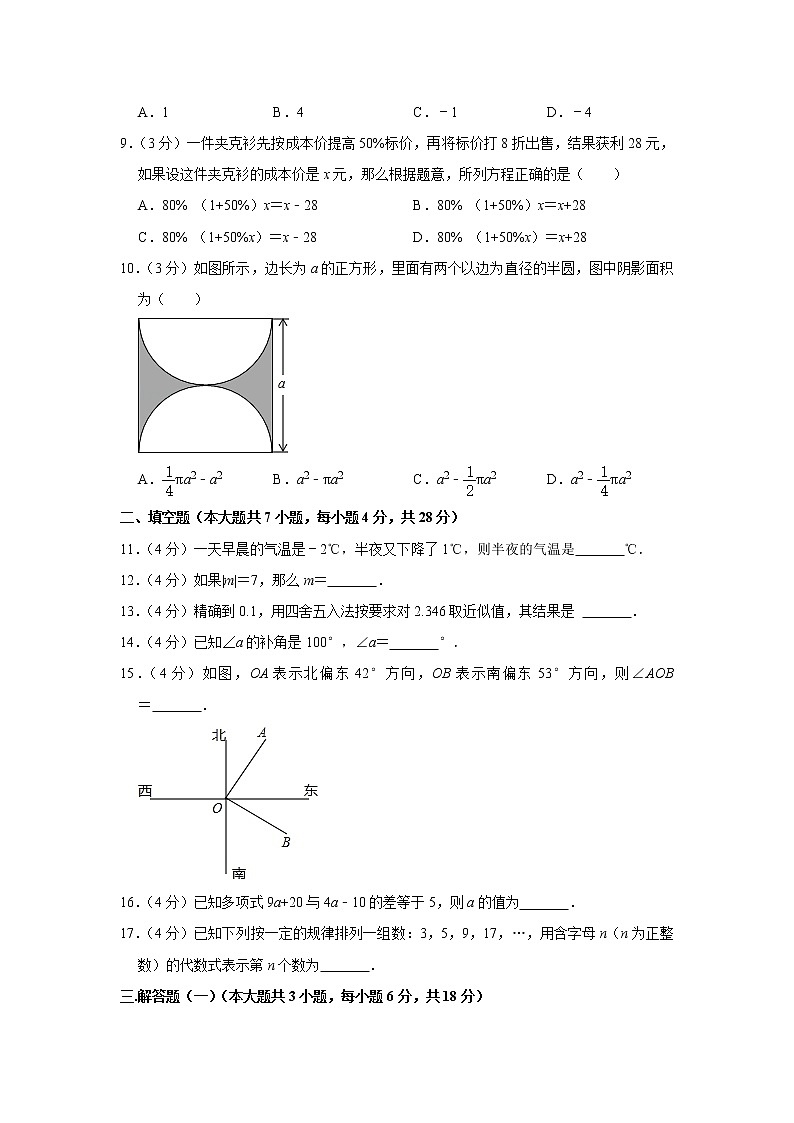
10.(3分)如图所示,边长为a的正方形,里面有两个以边为直径的半圆,图中阴影面积为( )
A.πa2﹣a2 B.a2﹣πa2 C.a2﹣πa2 D.a2﹣πa2
二、填空题(本大题共7小题,每小题4分,共28分)
11.(4分)一天早晨的气温是﹣2℃,半夜又下降了1℃,则半夜的气温是 ℃.
12.(4分)如果|m|=7,那么m= .
13.(4分)精确到0.1,用四舍五入法按要求对2.346取近似值,其结果是 .
14.(4分)已知∠a的补角是100°,∠a= °.
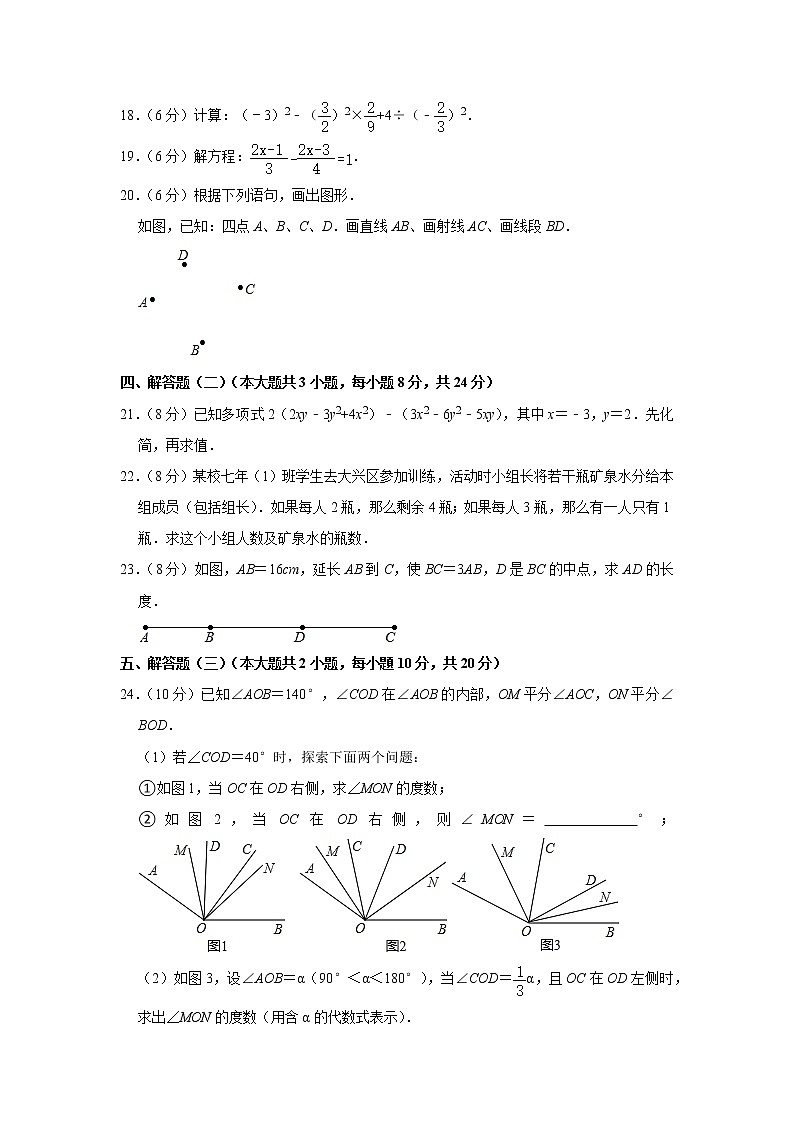
15.(4分)如图,OA表示北偏东42°方向,OB表示南偏东53°方向,则∠AOB= .
16.(4分)已知多项式9a+20与4a﹣10的差等于5,则a的值为 .
17.(4分)已知下列按一定的规律排列一组数:3,5,9,17,…,用含字母n(n为正整数)的代数式表示第n个数为 .
三.解答题(一)(本大题共3小题,每小题6分,共18分)
18.(6分)计算:(﹣3)2﹣()2×+4÷(﹣)2.
19.(6分)解方程:.
20.(6分)根据下列语句,画出图形.
如图,已知:四点A、B、C、D.画直线AB、画射线AC、画线段BD.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.(8分)已知多项式2(2xy﹣3y2+4x2)﹣(3x2﹣6y2﹣5xy),其中x=﹣3,y=2.先化简,再求值.
22.(8分)某校七年(1)班学生去大兴区参加训练,活动时小组长将若干瓶矿泉水分给本组成员(包括组长).如果每人2瓶,那么剩余4瓶;如果每人3瓶,那么有一人只有1瓶.求这个小组人数及矿泉水的瓶数.
23.(8分)如图,AB=16cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度.
五、解答题(三)(本大题共2小题,每小題10分,共20分)
24.(10分)已知∠AOB=140°,∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=40°时,探索下面两个问题:
①如图1,当OC在OD右侧,求∠MON的度数;
②如图2,当OC在OD右侧,则∠MON= °;
(2)如图3,设∠AOB=α(90°<α<180°),当∠COD=α,且OC在OD左侧时,求出∠MON的度数(用含α的代数式表示).
25.(10分)如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒5个单位长度的速度沿着数轴向左匀速运动,动点Q从点B(与点P同时)出发,设运动时间为t秒(t>0).
(1)数轴上点B对应的数为 ,AP的长为 ,点P对应的数是 (可用含t的式子表示);
(2)动点Q以每秒2个单位长度的速度,沿着数轴向左匀速运动.当点P追上点Q时,需多少时间?
(3)动点Q沿着数轴以每秒3个单位长度的速度作匀速运动,当点P与点Q相距5个单位长度时,直接写出运动时间t的值.
2019-2020学年广东省汕头市金平区七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本题共10小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个是正确的,请将答题卡上对应的小题所选的选项涂黑.
1.(3分)3的相反数是( )
A. B. C.3 D.﹣3
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.
【解答】解:3的相反数是﹣3,
故选:D.
2.(3分)过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )
A.3.12×105 B.3.12×106 C.31.2×105 D.0.312×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将3120000用科学记数法表示为:3.12×106.
故选:B.
3.(3分)把弯曲的河道改直,能够缩短航程,这样做的道理是( )
A.两点之间,射线最短 B.两点确定一条直线
C.两点之间,直线最短 D.两点之间,线段最短
【分析】根据两点之间线段最短即可得出答案.
【解答】解:由两点之间线段最短可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,
故选:D.
4.(3分)下列各数中,在﹣2和0之间的数是( )
A.﹣1 B.1 C.﹣3 D.3
【分析】根据有理数的大小比较法则比较即可.
【解答】解:A、﹣2<﹣1<0,故本选项正确;
B、1>0,1不在﹣2和0之间,故本选项错误;
C、﹣3<﹣2,﹣3不在﹣2和0之间,故本选项错误;
D、3>0,3不在﹣2和0之间,故本选项错误;
故选:A.
5.(3分)由五个小立方体搭成如图的几何体,从正面看到的平面图形是( )
A. B.
C. D.
【分析】找到从正面看所得到的图形即可.
【解答】解:从正面可看到三列正方形的个数依次为2,1,1.
故选:C.
6.(3分)下列方程中,解为x=2的是( )
A.2x=6 B.(x﹣3)(x+2)=0
C.x2=3 D.3x﹣6=0
【分析】把x=2代入各个方程,判断方程的左、右两边是否相等即可判断.
【解答】解:A、把x=2代入,左边=4≠右边,则不是方程的解,选项错误;
B、把x=2代入方程,左边=﹣4≠右边,则不是方程的解,选项错误;
C、把x=2代入方程,左边=4≠右边,则不是方程的解,选项错误;
D、把x=2代入方程,左边=0=右边,则是方程的解,选项正确.
故选:D.
7.(3分)下列运算中,正确的是( )
A.3a+2b=5ab B.3a2b﹣3ba2=0
C.2a3+3a2=5a5 D.5b2﹣4b2=1
【分析】直接利用合并同类项法则分别化简得出答案.
【解答】解:A、3a+2b无法计算,故此选项错误;
B、3a2b﹣3ba2=0,正确;
C、2a3+3a2,无法计算,故此选项错;
D、5b2﹣4b2=b2,故此选项错误;
故选:B.
8.(3分)如果a2﹣3b﹣1=0,那么多项式2a2﹣6b+2的值等于( )
A.1 B.4 C.﹣1 D.﹣4
【分析】将a2﹣3b﹣1做为整体代入所求代数式进行计算即可.
【解答】解:设m=a2﹣3b﹣1
∴2a2﹣6b+2=2(a2﹣3b﹣1)+4
=2×0+4=4.
即所求式为:4.
9.(3分)一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.80% (1+50%)x=x﹣28 B.80% (1+50%)x=x+28
C.80% (1+50%x)=x﹣28 D.80% (1+50%x)=x+28
【分析】根据售价的两种表示方法解答,关系式为:标价×80%=进价+28,把相关数值代入即可.
【解答】解:由题意得,标价为:x(1+50%),
八折出售的价格为:(1+50%)x×80%;
∴可列方程为:(1+50%)x×80%=x+28,
故选:B.
10.(3分)如图所示,边长为a的正方形,里面有两个以边为直径的半圆,图中阴影面积为( )
A.πa2﹣a2 B.a2﹣πa2 C.a2﹣πa2 D.a2﹣πa2
【分析】根据图形可知阴影部分的面积等于正方形的面积﹣圆的面积.
【解答】解:阴影部分的面积=a2﹣π()2=a2﹣πa2,
故选:D.
二、填空题(本大题共7小题,每小题4分,共28分)
11.(4分)一天早晨的气温是﹣2℃,半夜又下降了1℃,则半夜的气温是 ﹣3 ℃.
【分析】直接利用有理数的加减运算法则计算得出答案.
【解答】解:由题意可得:
半夜的气温是:﹣2﹣1=﹣3(℃).
故答案为:﹣3.
12.(4分)如果|m|=7,那么m= 7或﹣7 .
【分析】根据数轴上的点到原点的距离相等的点表示的数有两个,可得答案.
【解答】解:|m|=7,
m=±7,
故答案为:7或﹣7.
13.(4分)精确到0.1,用四舍五入法按要求对2.346取近似值,其结果是 2.3 .
【分析】近似数精确到哪一位,应当看末位数字实际在哪一位.
【解答】解:用四舍五入法按要求对2.346取近似值,其结果是2.3.
故答案为:2.3.
14.(4分)已知∠a的补角是100°,∠a= 80 °.
【分析】如果两个角的和等于180°(平角),就说这两个角互为补角.由此定义即可求解.
【解答】解:∵∠a的补角是100°,
∴∠α=180°﹣100°=80°,
故答案为:80°.
15.(4分)如图,OA表示北偏东42°方向,OB表示南偏东53°方向,则∠AOB= 85° .
【分析】利用角度的和差即可直接求解.
【解答】解:∠AOB=180°﹣42°﹣53°=85°.
故答案是:85°.
16.(4分)已知多项式9a+20与4a﹣10的差等于5,则a的值为 ﹣5 .
【分析】先根据差等于5列出方程,解方程即可.
【解答】解:由题意,得9a+20﹣(4a﹣10)=5,
∴9a+20﹣4a+10=5,
整理,得5a=﹣25,
∴a=﹣5.
故答案为:﹣5.
17.(4分)已知下列按一定的规律排列一组数:3,5,9,17,…,用含字母n(n为正整数)的代数式表示第n个数为 2n+1 .
【分析】首先发现3=2+1,5=4+1=22+1,9=8+1=23+1,17=16+1=24+1,…,由此得出规律解决问题.
【解答】解:3=2+1,
5=4+1=22+1,
9=8+1=23+1,
17=16+1=24+1,
…,
所以第n个数为2n+1.
故答案为:2n+1.
三.解答题(一)(本大题共3小题,每小题6分,共18分)
18.(6分)计算:(﹣3)2﹣()2×+4÷(﹣)2.
【分析】先算乘方,再把除法转化为乘法,再算乘法,最后算加减即可.
【解答】解:(﹣3)2﹣()2×+4÷(﹣)2
=9﹣×+4÷
=9﹣×+4×
=9﹣+9
=17.5.
19.(6分)解方程:.
【分析】方程去分母后,去括号,移项合并,将x系数化为1,即可求出解.
【解答】解:去分母得:4(2x﹣1)﹣3(2x﹣3)=12,
去括号得:8x﹣4﹣6x+9=12,
移项得:8x﹣6x=12+4﹣9,
合并得:2x=7,
解得:x=3.5.
20.(6分)根据下列语句,画出图形.
如图,已知:四点A、B、C、D.画直线AB、画射线AC、画线段BD.
【分析】根据直线、射线、线段的定义画图即可.
【解答】解:如图所示:
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.(8分)已知多项式2(2xy﹣3y2+4x2)﹣(3x2﹣6y2﹣5xy),其中x=﹣3,y=2.先化简,再求值.
【分析】原式去括号,合并同类项进行化简,然后代入求值.
【解答】解:原式=4xy﹣6y2+8x2﹣3x2+6y2+5xy
=5x2+9xy,
当x=﹣3,y=2时,
原式=5×(﹣3)2+9×(﹣3)×2
=5×9﹣54
=45﹣54
=﹣9.
22.(8分)某校七年(1)班学生去大兴区参加训练,活动时小组长将若干瓶矿泉水分给本组成员(包括组长).如果每人2瓶,那么剩余4瓶;如果每人3瓶,那么有一人只有1瓶.求这个小组人数及矿泉水的瓶数.
【分析】根据每人2瓶,那么剩余4瓶;如果每人3瓶,那么有一人只有1瓶,可以列出相应的方程,然后即可求得这个小组人数及矿泉水的瓶数.
【解答】解:设这个小组有x人,
2x+4=3(x﹣1)+1,
解得x=6,
∴2x+4=2×6+4=16,
答:这个小组有6人,有16瓶矿泉水.
23.(8分)如图,AB=16cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度.
【分析】由已知条件知BC=3AB=48,BD=BC=24,根据AD=AB+BD可求.
【解答】解:∵AB=16cm,
∴BC=3AB=3×16=48cm.
∵D是BC的中点,
∴BD=BC=×48=24cm.
∴AD=AB+BD=16+24=40cm.
五、解答题(三)(本大题共2小题,每小題10分,共20分)
24.(10分)已知∠AOB=140°,∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=40°时,探索下面两个问题:
①如图1,当OC在OD右侧,求∠MON的度数;
②如图2,当OC在OD右侧,则∠MON= 90 °;
(2)如图3,设∠AOB=α(90°<α<180°),当∠COD=α,且OC在OD左侧时,求出∠MON的度数(用含α的代数式表示).
【分析】(1)①根据角平分线的定义,得出∠AOM=∠AOC,∠BON=∠BOD,再根据∠AOB=140°,∠COD=40°,得出∠AOC+∠BOD=∠AOB+∠COD=180°,进而得出∠AOM+∠BON的度数,最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可;
②根据①中的方法进行计算,即可得出∠MON的度数;
(2)先根据角平分线的定义,得出∠AOM=∠AOC,∠BON=∠BOD,再根据∠AOB=α,∠COD=α,得出∠AOC+∠BOD=∠AOB﹣∠COD=α,进而得到∠AOM+∠BON的度数,最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可.
【解答】解:(1)①如图1,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=∠AOC,∠BON=∠BOD,
∴∠AOM+∠BON=(∠AOC+∠BOD),
∵∠AOB=140°,∠COD=40°,
∴∠AOC+∠BOD=∠AOB+∠COD=180°,
∴∠AOM+∠BON=×180°=90°,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=140°﹣90°=50°;
②当OC在OD右侧,如图2,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=∠AOC,∠BON=∠BOD,
∴∠AOM+∠BON=(∠AOC+∠BOD),
∵∠AOB=140°,∠COD=40°,
∴∠AOC+∠BOD=∠AOB﹣∠COD=100°,
∴∠AOM+∠BON=×100°=50°,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=140°﹣50°=90°,
故答案为:90°;
(2)∠MON的度数为α.
理由:如图3,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=∠AOC,∠BON=∠BOD,
∴∠AOM+∠BON=(∠AOC+∠BOD),
∵∠AOB=α,∠COD=α,
∴∠AOC+∠BOD=∠AOB﹣∠COD=α,
∴∠AOM+∠BON=×α=α,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α.
25.(10分)如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒5个单位长度的速度沿着数轴向左匀速运动,动点Q从点B(与点P同时)出发,设运动时间为t秒(t>0).
(1)数轴上点B对应的数为 ﹣4 ,AP的长为 5t ,点P对应的数是 6﹣5t (可用含t的式子表示);
(2)动点Q以每秒2个单位长度的速度,沿着数轴向左匀速运动.当点P追上点Q时,需多少时间?
(3)动点Q沿着数轴以每秒3个单位长度的速度作匀速运动,当点P与点Q相距5个单位长度时,直接写出运动时间t的值.
【分析】(1)根据点A对应的数为6,B是数轴上的一点,且AB=10,可得B点表示的数为6﹣10=﹣4;点P表示的数为6﹣6t;
(2)由点P追上点Q,列出方程,即可求解;
(3)分点Q沿着数轴向左,向右两种情况讨论,列出方程可求解.
【解答】解:(1)∵AB=10,点A对应的数为6,点B在点A的左侧,
∴点B对应的数为﹣4,
∵动点P从点A出发,以每秒5个单位长度的速度沿着数轴向左匀速运动,
∴AP=5t,
∴点P对应的数为6﹣5t;
故答案为:﹣4;5t;6﹣5t;
(2)由题意可得:5t=2t+10,
解得:t=,
答:经过s,点P追上点Q;
(3)若点Q沿着数轴向左运动时,由题意可得:5t﹣(3t+10)=5或(3t+10)﹣5t=5,
解得:t=或,
若点Q沿着数轴向右运动时,由题意可得:5t+2t=10﹣5或5t+2t=10+5,
解得:t=或,
综上所述:若点Q沿着数轴向左运动时,当t=或时,点P与点Q相距5个单位长度;若点Q沿着数轴向右运动时,当t=或时,点P与点Q相距5个单位长度.
2023-2024学年广东省汕头市金平区七年级(下)期末数学试卷(含详细答案解析): 这是一份2023-2024学年广东省汕头市金平区七年级(下)期末数学试卷(含详细答案解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省汕头市金平区2023-2024学年七年级下学期期末考试数学试卷: 这是一份广东省汕头市金平区2023-2024学年七年级下学期期末考试数学试卷,共4页。
2023-2024学年广东省汕头市金平区七年级(上)学期期末数学试题(含解析): 这是一份2023-2024学年广东省汕头市金平区七年级(上)学期期末数学试题(含解析),共15页。试卷主要包含了考生必须保持答题卡的整洁,已知关于的方程的解是,则的值为,下列去括号正确的是,下列说法正确的有等内容,欢迎下载使用。












