中考数学综合练习题48

这是一份中考数学综合练习题48，共16页。试卷主要包含了选择题，填空题[来，简答题等内容，欢迎下载使用。
中考数学综合练习题48
一、选择题(本题有10个小题，每小题3分，共30分)
1.统计显示，2017年底泰州市各类高中在校学生人数约是11.4万人，将11.4万用科学记数法表示应为( )
A. 11.4×104 B. 1.14×104 C. 1.14×105 D. 0.114×106
2.下列计算正确的是( )
A. 23+24=27 B. 23−24= C. 23×24=27 D. 23÷24=21
3.下列图形是中心对称图形的是( )

A. B. C. D.
4.下列各式的变形中，正确的是( )
A. (−x−y)(−x+y)=x2−y2 B. C. x2−4x+3=(x−2)2+1 D. x÷(x2+x)=+1
5.圆内接四边形ABCD中，已知∠A=70°，则∠C=( )
A. 20° B. 30° C. 70° D. 110°
6.若k＜＜k+1(k是整数)，则k=( )[来源:学科网ZXXK][来源:学.科.网Z.X.X.K]
A. 6 B. 7 C. 8 D. 9
7.某村原有林地108公顷，旱地54公顷，为保护环境，需把一部分旱地改造为林地，使旱地占林地面积的20%，设把x公顷旱地改为林地，则可列方程( )
A. 54−x=20%×108 B. 54−x=20%×(108+x) C. 54+x=20%×162 D. 108−x=20%(54+x)
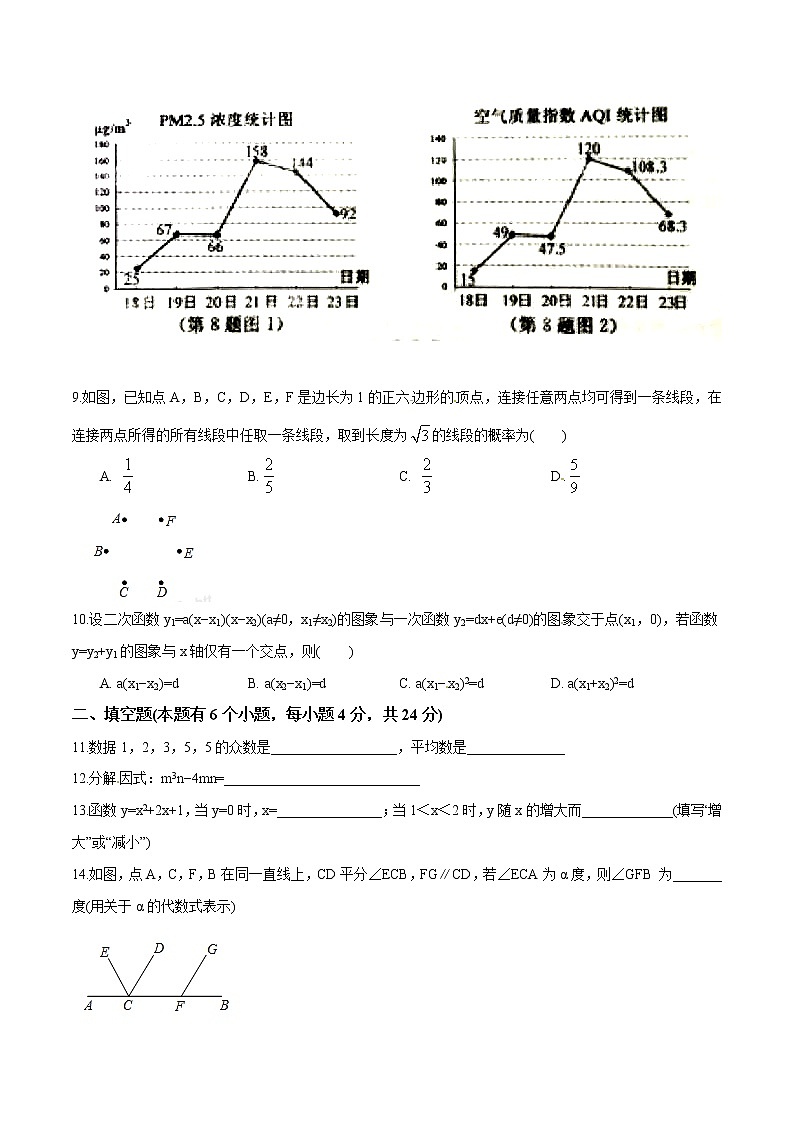
8.如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”)，由图可得下列说法：①18日的PM2.5浓度最低；②这六天中PM2.5浓度的中位数是112µg/cm2；③这六天中有4天空气质量为“优良”；④空气质量指数AQI与PM2.5浓度有关，其中正确的说法是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
[来源:学科网ZXXK]
9.如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段，在连接两点所得的所有线段中任取一条线段，取到长度为的线段的概率为( )
A. B. C. D. [来源:Zxxk.Com]

10.设二次函数y1=a(x−x1)(x−x2)(a≠0，x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1，0)，若函数y=y2+y1的图象与x轴仅有一个交点，则( )
A. a(x1−x2)=d B. a(x2−x1)=d C. a(x1−x2)2=d D. a(x1+x2)2=d
二、填空题(本题有6个小题，每小题4分，共24分)[来
11.数据1，2，3，5，5的众数是__________________，平均数是______________
12.分解因式：m3n−4mn=____________________________
13.函数y=x2+2x+1，当y=0时，x=_______________；当1＜x＜2时，y随x的增大而_____________(填写“增大”或“减小”)
14.如图，点A，C，F，B在同一直线上，CD平分∠ECB，FG∥CD，若∠ECA为α度，则∠GFB 为_______度(用关于α的代数式表示)
[来源:学科网]
15.在平面直角坐标系中，O为坐标原点，设点P(1，t)在反比例函数y=的图象上，过点P作直线l与x轴平行，点Q在直线l上，满足QP=OP，若反比例函数y=的图象经过点Q，则k=_____
16.如图，在四边形纸片ABCD中，AB=BC，AD=CD，∠A=∠C=90°，∠B=150°，将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平，若铺平后的图形中有一个是面积为2的平行四边形，则CD=__________

三、简答题(本题有7个小题，共66分)
17.(6分)杭州市推行垃圾分类已经多年，但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾，如图是杭州市某一天收到的厨余垃圾的统计图
(1)、试求出m的值[来源:Zxxk.Com]
(2)、杭州市那天共收到厨余垃圾约200吨，请计算其中混杂着的玻璃类垃圾的吨数

18.(8分)如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M、N分别在AB、AC边上，AM=2MB，AN=2NC，求证：DM=DN

19.(8分)如图1，☉O的半径为r(r>0)，若点P′在射线OP上，满足OP′•OP=r2，则称点P′是点P关于☉O的“反演点”，如图2，☉O的半径为4，点B在☉O上，∠BOA=60°，OA=8，若点A′、B′分别是点A，B关于☉O的反演点，求A′B′的长

20.(10分)设函数y=(x−1)[(k−1)x+(k−3)](k是常数)
(1)、当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时函数的图象
(2)、根据图象，写出你发现的一条结论
(3)、将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值:

21.(10分)“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度
(1)、用记号(a，b，c)(a≤b≤c)表示一个满足条件的三角形，如(2，3，3)表示边长分别为2，3，3个单位长度的一个三角形，请列举出所有满足条件的三角形
(2)、用直尺和圆规作出三边满足a＜b＜c的三角形(用给定的单位长度，不写作法，保留作图痕迹)

22.(12分)如图，在△ABC中(BC>AC)，∠ACB=90°，点D在AB边上，DE⊥AC于点E
(1)、若，AE=2，求EC的长
(2)、设点F在线段EC上，点G在射线CB上，以F，C，G为顶点的三角形与△EDC有一个锐角相等，FG交CD于点P，问：线段CP可能是△CFG的高线还是中线？或两者都有可能？请说明理由

23.(12分)方成同学看到一则材料，甲开汽车，乙骑自行车从M地出发沿一条公路匀速前往N地，设乙行驶的时间为t(h)，甲乙两人之间的距离为y(km)，y与t的函数关系如图1所示，方成思考后发现了图1的部分正确信息，乙先出发1h，甲出发0.5小时与乙相遇，⋯⋯，请你帮助方成同学解决以下问题：
(1)、分别求出线段BC，CD所在直线的函数表达式
(2)、当20＜y＜30时，求t的取值范围
(3)、分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式，并在图2所给的直角坐标系中分别画出它们的图象
(4)、丙骑摩托车与乙同时出发，从N地沿同一条公路匀速前往M地，若丙经过h与乙相遇，问丙出发后多少时间与甲相遇？














答案解析
一、选择题(本题有10个小题，每小题3分，共30分)
1.统计显示，2017年底泰州市各类高中在校学生人数约是11.4万人，将11.4万用科学记数法表示应为( )
A. 11.4×104 B. 1.14×104 C. 1.14×105 D. 0.114×106
【答案】C
考点：科学计数法
2.下列计算正确的是( )
A. 23+24=27 B. 23−24= C. 23×24=27 D. 23÷24=21
【答案】C
【解析】
试题分析：同底数幂相乘，底数不变，指数相加；同底数幂相除，底数不变，指数相减.根据幂的计算法则可得：+=24；－=－8；×=；÷=.
考点：幂的计算.
3.下列图形是中心对称图形的是( )
【答案】A
【解析】
试题分析：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与另一个图形重合，这样的图形叫做中心对称图形.根据定义可得A为中心对称图形.
考点：中心对称图形
4.下列各式的变形中，正确的是( )
A. (−x−y)(−x+y)=x2−y2 B. C. x2−4x+3=(x−2)2+1 D. x÷(x2+x)=+1
【答案】A
【解析】
试题分析：根据平方差公式可得A正确；根据分式的减法法则可得：B=；根据完全平方公式可得：C=－1；根据单项式除以多项式的法则可得：D=.
考点：多项式的乘法、除法计算，完全平方公式.
5.圆内接四边形ABCD中，已知∠A=70°，则∠C=( )
A. 20° B. 30° C. 70° D. 110°[来源:学+科+网]
【答案】D
考点：圆内接四边形的性质.
6.若k＜＜k+1(k是整数)，则k=( )
A. 6 B. 7 C. 8 D. 9
【答案】D
【解析】
试题分析：∵81＜90＜100，∴＜＜，即9＜＜10，则k=9.
考点：二次根式的估算.
7.某村原有林地108公顷，旱地54公顷，为保护环境，需把一部分旱地改造为林地，使旱地占林地面积的20%，设把x公顷旱地改为林地，则可列方程( )
A. 54−x=20%×108 B. 54−x=20%×(108+x) C. 54+x=20%×162 D. 108−x=20%(54+x)
【答案】B
【解析】
试题分析：根据题意可得改造后旱地的面积为(54－x)公顷；林地的面积为(108+x)公顷，根据题意可得等式为：旱地的面积=林地的面积×20%，即54－x=20%×(108+x).
考点：一元一次方程的应用.
8.如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”)，由图可得下列说法：①18日的PM2.5浓度最低；②这六天中PM2.5浓度的中位数是112µg/cm2；③这六天中有4天空气质量为“优良”；④空气质量指数AQI与PM2.5浓度有关，其中正确的说法是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④

【答案】C
【解析】
试题分析：根据折线统计图可得：18日的PM2.5浓度最低；这六天中PM2.5浓度的中位数是79.5µg/cm2；这六天中有4天空气质量为“优良”；空气质量指数AQI与PM2.5浓度有关.即①③④正确.
考点：折线统计图.
9.如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段，在连接两点所得的所有线段中任取一条线段，取到长度为的线段的概率为( )
A. B. C. D.

【答案】B
【解析】
试题分析：根据题意可得所有的线段有15条，长度为的线段有AE、AC、FD、FB、EC、BD共6条，则P(长度为的线段)=.
考点：概率的计算.
10.设二次函数y1=a(x−x1)(x−x2)(a≠0，x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1，0)，若函数y=y2+y1的图象与x轴仅有一个交点，则( )
A. a(x1−x2)=d B. a(x2−x1)=d C. a(x1−x2)2=d D. a(x1+x2)2=d
【答案】B
考点：二次函数与一元二次方程、因式分解.
二、填空题(本题有6个小题，每小题4分，共24分)[来
11.数据1，2，3，5，5的众数是__________________，平均数是______________
【答案】5；
【解析】
试题分析：众数是指出现次数最多的数字，本题中的众数为5；平均数=(1+2+3+5+5)÷5=
考点：众数和平均数的计算.
12.分解因式：m3n−4mn=____________________________
【答案】mn(m+2)(m－2)
考点：因式分解.
13.函数y=x2+2x+1，当y=0时，x=_______________；当1＜x＜2时，y随x的增大而_____________(填写“增大”或“减小”)
【答案】－1；增大.
【解析】
试题分析：将y=0代入函数，求出一元二次方程的解；对于开口向上的函数，当x＞对称轴时，y随x的增大而增大，当x＜对称轴时，y随x的增大而减小.当y=0时，即+2x+1=0，解得：x=－1；根据函数解析式可得函数的对称轴为直线x=－1，则当1＜x＜2时，y随x的增大而增大.
考点：二次函数的性质.
14.如图，点A，C，F，B在同一直线上，CD平分∠ECB，FG∥CD，若∠ECA为α度，则∠GFB 为_______度(用关于α的代数式表示)

【答案】90°－α
考点：平行线的性质、角平分线的性质.
15.在平面直角坐标系中，O为坐标原点，设点P(1，t)在反比例函数y=的图象上，过点P作直线l与x轴平行，点Q在直线l上，满足QP=OP，若反比例函数y=的图象经过点Q，则k=_____
【答案】2+2；2－2
【解析】
试题分析：将点P代入反比例函数解析式可得点P的坐标为(1,2)、∵PQ∥x轴，则点Q的纵坐标为2，根据点P的坐标可得OP=.当点Q在点P的左边时，点Q的坐标为(1－，2)，则k=2－2；当点Q在点P的右边时，点Q的坐标为(1+，2)，则k=2+2.
考点：反比例函数的性质.
16.如图，在四边形纸片ABCD中，AB=BC，AD=CD，∠A=∠C=90°，∠B=150°，将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平，若铺平后的图形中有一个是面积为2的平行四边形，则CD=__________

【答案】2+4；2+

考点：平行四边形的性质.
三、简答题(本题有7个小题，共66分)
17.(6分)杭州市推行垃圾分类已经多年，但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾，如图是杭州市某一天收到的厨余垃圾的统计图
(1)、试求出m的值[来源:Zxxk.Com]
(2)、杭州市那天共收到厨余垃圾约200吨，请计算其中混杂着的玻璃类垃圾的吨数

【答案】69.02；1.8吨.
【解析】
试题分析：根据扇形统计图求出m的值；根据扇形统计图可得玻璃类垃圾=厨余垃圾×0.9%得到答案.
试题解析：(1)、m=100－(22.39+0.9+7.55+0.15)=69.01
(2) 、200×0.9%=1.8(吨)
答：其中混杂着的玻璃类垃圾的吨数为1.8吨.
考点：扇形统计图.
18.(8分)如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M、N分别在AB、AC边上，AM=2MB，AN=2NC，求证：DM=DN

【答案】略.
考点：三角形全等的性质.
19.(8分)如图1，☉O的半径为r(r>0)，若点P′在射线OP上，满足OP′•OP=r2，则称点P′是点P关于☉O的“反演点”，如图2，☉O的半径为4，点B在☉O上，∠BOA=60°，OA=8，若点A′、B′分别是点A，B关于☉O的反演点，求A′B′的长

【答案】2
【解析】
试题分析：首先根据题意得出OA′的长度，同理得出OB′的长度，即B点的反演点B′与B重合.设OA交圆于点M，连接B′M.根据∠BOA=60°，OM=OB′得出△OB′M为正三角形，又根据A′为OM的中点得出A′B′⊥OM，根据勾股定理求出A′B′的长度.
试题解析：∵OA′·OA=16，OA=8 ∴OA′=2 同理可得OB′=4 即B点的反演点B′与B重合
设OA交圆于点M，连接B′M ∵∠BOA=60°，OM=OB′ ∴△OB′M为正三角形
又∵点A′为OM的中点 ∴A′B′⊥OM
根据勾股定理，得： 即16=4+ 解得：A′B′=2
考点：勾股定理、新定义型题.
20.(10分)设函数y=(x−1)[(k−1)x+(k−3)](k是常数)
(1)、当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时函数的图象
(2)、根据图象，写出你发现的一条结论
(3)、将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值:
[来源:学§科§网Z§X§X§K]
【答案】略；略；－2.
试题解析：(1)、根据题意可得函数图象为：

(2) 、①、图象都经过点(1,0)和点(－1,4)；②、图象总交x轴与点(1,0)；③、k取0和2时的函数图象关于点(0,2)成中心对称；
(3) 、平移后的函数的表达式为： ∴当x=－3时，函数的最小值为－2.
考点：函数图象的性质.
21.(10分)“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度[来源:学科网ZXXK]
(1)、用记号(a，b，c)(a≤b≤c)表示一个满足条件的三角形，如(2，3，3)表示边长分别为2，3，3个单位长度的一个三角形，请列举出所有满足条件的三角形
(2)、用直尺和圆规作出三边满足a＜b＜c的三角形(用给定的单位长度，不写作法，保留作图痕迹)

【答案】略.
、只有a=2，b=3，c=4的一个三角形，如图所示的△ABC就是满足条件的三角形

考点：三角形的三边关系，三角形的作法.[来源:Z,xx,k.Com]
22.(12分)如图，在△ABC中(BC>AC)，∠ACB=90°，点D在AB边上，DE⊥AC于点E
(1)、若，AE=2，求EC的长
(2)、设点F在线段EC上，点G在射线CB上，以F，C，G为顶点的三角形与△EDC有一个锐角相等，FG交CD于点P，问：线段CP可能是△CFG的高线还是中线？或两者都有可能？请说明理由

【答案】6；略.
【解析】
试题分析：根据∠ACB=90°，DE⊥AC得出DE∥BC，从而得到线段之间的比值，然后求出CE的长度；(2)、①若∠CF=∠ECD 此时线段C为Rt△CF的F边上的中线，根据∠CF=∠ECD得出∠CF=∠FC，又根据∠CF+∠CF=90°， ∠FC+∠C=90°得出∠CF=∠C即C=，则可以得出C=F=，从而得出结论；②、若∠CF=∠EDC 此时线段此时线段C为Rt△CF的F边上的高线；③、当CD为∠ACB的平分线时，CP既是△CFG的FG边上的高线又是中线.
试题解析：(1)、∵∠ACB=Rt∠ DE⊥AC ∴DE∥BC ∴
∵，AE=2 ∴ 解得：EC=6.
②、若∠CF=∠EDC 此时线段此时线段C为Rt△CF的F边上的高线
证明：∵∠CF=∠EDC ∵DE⊥AC ∴∠EDC=90° ∴∠EDC+∠ECD=90°
∴∠ECD+∠CF=∠ECD+∠EDC=90° ∴C⊥F
即线段C为Rt△CF的F边上的高线
③、当CD为∠ACB的平分线时，CP既是△CFG的FG边上的高线又是中线.
考点：等腰三角形的性质、角度之间的关系.
23.(12分)方成同学看到一则材料，甲开汽车，乙骑自行车从M地出发沿一条公路匀速前往N地，设乙行驶的时间为t(h)，甲乙两人之间的距离为y(km)，y与t的函数关系如图1所示，方成思考后发现了图1的部分正确信息，乙先出发1h，甲出发0.5小时与乙相遇，⋯⋯，请你帮助方成同学解决以下问题：
(1)、分别求出线段BC，CD所在直线的函数表达式
(2)、当20＜y＜30时，求t的取值范围
(3)、分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式，并在图2所给的直角坐标系中分别画出它们的图象
(4)、丙骑摩托车与乙同时出发，从N地沿同一条公路匀速前往M地，若丙经过h与乙相遇，问丙出发后多少时间与甲相遇？

【答案】(1)、直线BC：y=40t－60；直线CD：y=－20+80；(2)、2＜t＜或＜t＜3；(3)、略；(4)、.
试题解析：(1)、直线BC的函数表达式为：y=40t－60；直线CD的函数表达式为：y=－20t+80
(2) 、OA的函数表达式为：y=20t(0≤t≤1) ∴点A的纵坐标为20
当20＜y＜30时，即20＜40t－60＜30或20＜－20t+80＜30[来源:学科网]
解得：2＜t＜或＜t＜3；
(3) 、=60t－60(1≤t≤) =20t(0≤t≤4) 所画函数图象如图：

(4) 、当t=时，= 丙距M地的路程与时间的函数表达式为：=－40t+80(0≤t≤2)
=－40t+80与=60t－60的图象交点的横坐标为 ∴丙出发小时与甲相遇.
考点：一次函数的实际应用.