八年级数学 培优竞赛 专题20 正方形 讲义学案

这是一份八年级数学 培优竞赛 专题20 正方形 讲义学案，文件包含八年级数学培优竞赛专题20正方形讲义doc、八年级数学培优竞赛专题20正方形_答案doc等2份学案配套教学资源，其中学案共11页， 欢迎下载使用。
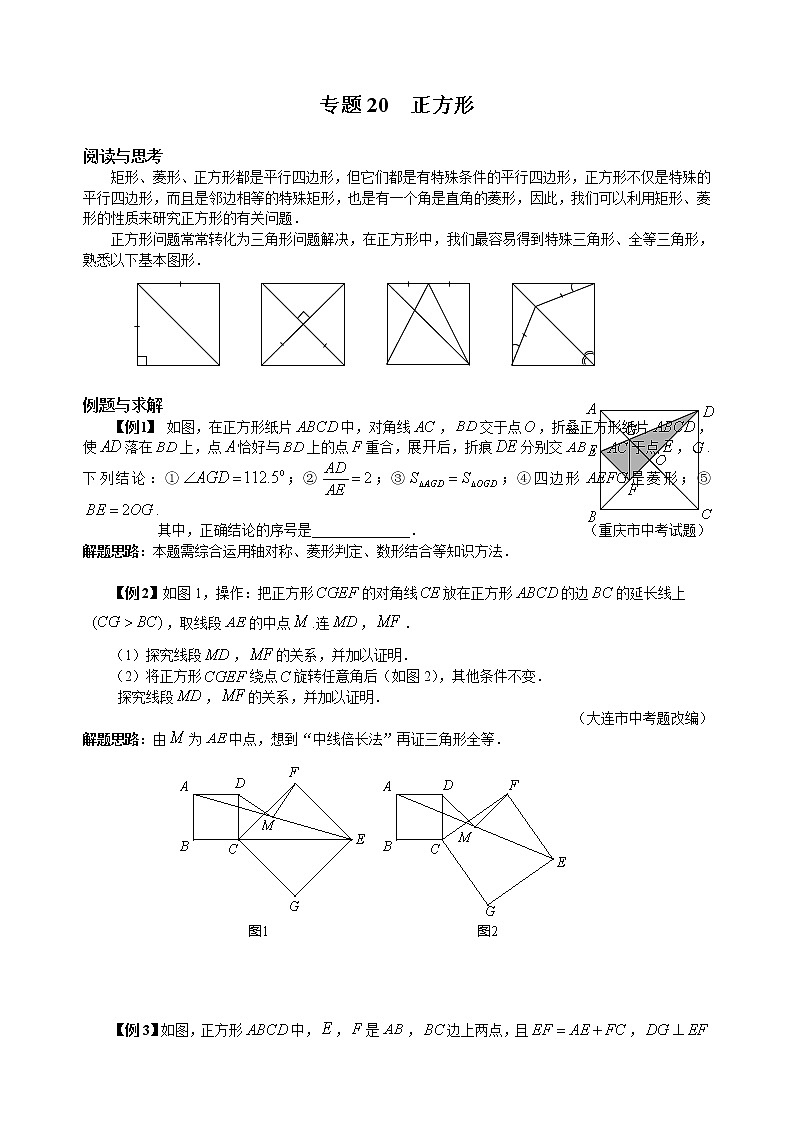
专题20  正方形 阅读与思考    矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的平行四边形，而且是邻边相等的特殊矩形，也是有一个角是直角的菱形，因此，我们可以利用矩形、菱形的性质来研究正方形的有关问题．正方形问题常常转化为三角形问题解决，在正方形中，我们最容易得到特殊三角形、全等三角形，熟悉以下基本图形．      例题与求解【例l】 如图，在正方形纸片中，对角线，交于点，折叠正方形纸片，使落在上，点恰好与上的点重合，展开后，折痕分别交，于点，.下列结论：①；②；③；④四边形是菱形；⑤.其中，正确结论的序号是______________．                       （重庆市中考试题）解题思路：本题需综合运用轴对称、菱形判定、数形结合等知识方法．                                                                                                    【例2】如图1，操作：把正方形的对角线放在正方形的边的延长线上，取线段的中点.连，．   （1）探究线段，的关系，并加以证明．   （2）将正方形绕点旋转任意角后（如图2），其他条件不变．    探究线段，的关系，并加以证明．                                                                      （大连市中考题改编）解题思路：由为中点，想到“中线倍长法”再证三角形全等．                     【例3】如图，正方形中，，是，边上两点，且，于，求证：.                                                               （重庆市竞赛试题）    解题思路：构造的线段是解本例的关键．                                                                                                                                                 【例4】  如图，正方形被两条与边平行的线段、分割成四个小矩形，是与的交点，若矩形的面积恰是矩形面积的2倍，试确定的大小，并证明你的结论．                                                                       （北京市竞赛试题）    解题思路：先猜测的大小，再作出证明，解题的关键是由条件及图形推出隐含的线段间的关系．                                                               【例5】 如图，在正方形中，，分别是边，上的点，满足，分别与对角线交于点．             求证：（1）；     （2）．                         （四川省竞赛试题）     解题思路：对于（1），可作辅助线，创造条件，再通过三角形全等，即可解答；对于（2），很容易联想到直角三角形三边关系．                                                                 【例6】已知 ：正方形中，，绕点顺时针旋转，它的两边分别交，（或它们的延长线）于点． 当绕点旋转到时（如图1），易证．（1）当绕点旋转到时（如图2），线段和之间有怎样的数量关系？写出猜想，并加以证明；（2）当绕点旋转到如图3的位置时，线段和之间又有怎样的数量关系？请直接写出你的猜想．                                                                  （黑龙江省中考试题）      解题思路：对于（2），构造是解题的关键．                           能力训练A级1. 如图，若四边形是正方形，是等边三角形，则的度数为__________.（北京市竞赛试题）2. 四边形的对角线相交于点，给出以下题设条件：①；②；③；④．其中，能判定它是正方形的题设条件是______________.  （把你认为正确的序号都填在横线上）           （浙江省中考试题）                 3．如图，边长为1的两个正方形互相重合，按住一个不动，将另一个绕顶点顺时针旋转，则这两个正方形重叠部分的面积是__________.  （青岛市中考试题）                第1题图                                第3题图                 第4题图 4.如图，是正方形内一点，将绕点顺时针方向旋转至能与重合，若，则=__________.                                             （河南省中考试题）                                                5.将个边长都为的正方形按如图所示摆放，点分别是正方形的中心，则个正方形重叠形成的重叠部分的面积和为(     )A .        B．         C.         D.                                                        （晋江市中考试题）                     第5题图                              第6题图       6. 如图，以的斜边为一边在的同侧作正方形，设正方形的中心为，连接，如果，则的长为(     )A . 12            B．8             C.              D.      （浙江省竞赛试题）                                                 7．如图，正方形中，，那么是(      )A .            B．             C.               D.      8．如图，正方形的面积为256，点在上，点在的延长线上，的面积为200，则的值是(     )A．15             B．12               C．11               D．10                                                        9．如图，在正方形中，是边的中点，与交于点，求证：．                                                                                                                  10. 如图，在正方形中，是边的中点，是上的一点，且 ．求证：平分．                                                        11. 如图，已知是正方形对角线上一点，分别是垂足．求证：．（扬州市中考试题）                                                                   12.（1）如图1，已知正方形和正方形，在同一条直线上，为线段的中点．探究：线段的关系．（2）如图2，若将正方形绕点顺时针旋转，使得正方形的对角线在正方形的边的延长线上，为的中点．试问：（1）中探究的结论是否成立？若成立，请证明；若不成立，请说明理由．（大连市中考试题）                                 图1                                     图2    B级1. 如图，在四边形中，，于，若四边形的面积为8，则的长为__________.2.如图，是边长为1的正方形内一点，若，则__________.                                                                        （北京市竞赛试题）3.如图，在中，，以为一边向三角形外作正方形，正方形的中心为，且，则的长为__________.（“希望杯”邀请赛试题）4.如图：边长一定的正方形，是上一动点，交于，过作交于点，作于点，连接，下列结论：①；②；③；④为定值，其中一定成立的是(      )A . ①②③            B．①②④           C. ②③④             D. ①②③④     5.如图，是正方形，，是菱形，则与度数的比值是(      )A . 3                  B．4                C. 5                  D. 不是整数6.一个周长为20的正方形内接于一个周长为28的正方形，那么从里面正方形的顶点到外面正方形的顶点的最大距离是(      )A .          B．          C. 8           D.          E.（美国高中考试题）7.如图，正方形中，，是的中点，设，在上取一点，使，则的长度等于 (      )A . 1                  B．2                C. 3                  D. （“希望杯”邀请赛试题）8.已知正方形中，是中点，是延长线上一点，且交平分线于（如图1）（1）求证：；（2）若将上述条件中的“是中点”改为“是上任意一点”其余条件不变（如图2），（1）中结论是否成立？如果成立，请证明；如果不成立，请说明理由；（3）如图2，点是的延长线上（除点外）的任意一点，其他条件不变，则（1）中结论是否成立？如果成立，请证明；如果不成立，请说明理由；                                                                   （临汾市中考试题）    `9.已知求证：．     10.如果，点分别在正方形的边上，已知的周长等于正方形周长的一半，求的度数．                                  （“祖冲之杯”邀请赛试题）                                                      11.如图，两张大小适当的正方形纸片，重叠地放在一起，重叠部分是一个凸八边形，对角线分这个八边形为四个小的凸四边形，请你证明：，且．（北京市竞赛试题）                                             12.如图，正方形内有一点，以为边向外作正方形和正方形，连接．求证：．（武汉市竞赛试题）