

八年级数学 培优竞赛 专题28 整体与完形 讲义学案
展开专题28 整体与完形
阅读与思考
许多几何问题,常因图形复杂、不规则而给解题带来困难,这些复杂、不规则的图形,从整体考虑,可看作某种图形的一部分,如果将它们补充完整,就可得到常见的特殊图形,那么就能利用特殊图形的特殊性质转化问题,这就是解几何问题的补形法,常见的补形方法有:
- 将原图形补形为最能体现相关定理、推论、公理的基本图形;
- 将原图形补形为等腰三角形、等边三角形、直角三角形等特殊三角形;
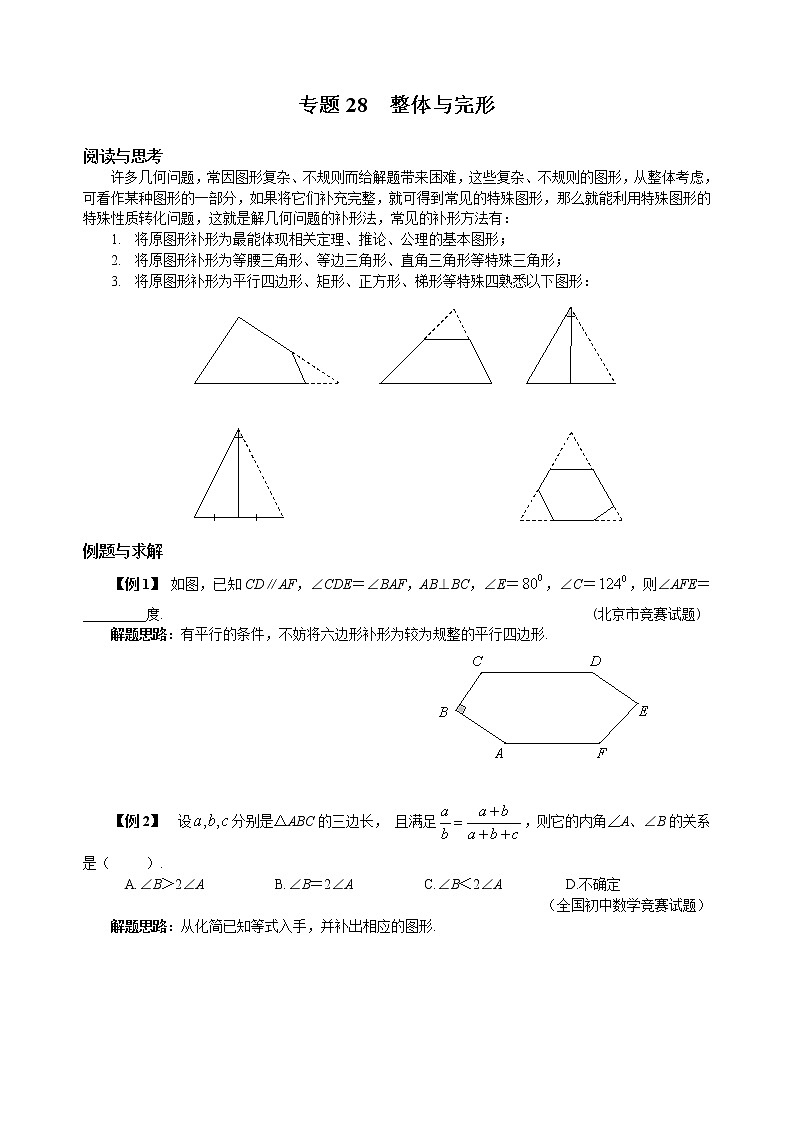
- 将原图形补形为平行四边形、矩形、正方形、梯形等特殊四熟悉以下图形:
例题与求解
【例1】 如图,已知CD∥AF,∠CDE=∠BAF,AB⊥BC,∠E=,∠C=,则∠AFE=_________度. (北京市竞赛试题)
解题思路:有平行的条件,不妨将六边形补形为较为规整的平行四边形.
【例2】 设分别是△ABC的三边长, 且满足,则它的内角∠A、∠B的关系是( ).
A.∠B>2∠A B.∠B=2∠A C.∠B<2∠A D.不确定
(全国初中数学竞赛试题)
解题思路:从化简已知等式入手,并补出相应的图形.
【例3】 如图1,BD,CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F,G,连结FG,延长AF,AG,与直线BC相交,易证.
若(1)BD,CE分别是△ABC的内角平分线(如图2);(2)BD为∠ABC的内角平分线;(3)CE为△ABC的外角平分线(如图3),则在图2、图3两种情况下,线段FG与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明.
(黑龙江省中考试题)
解题思路:既有平分线又有垂线,联想到等腰三角形性质,考虑将图形补成等腰三角形.
【例4】 如图,四边形ABCD中,∠ABC=,∠BCD=,AB=,BC=,
CD=,求AD的长. (全国初中数学竞赛试题)
解题思路:由于四边形ABCD是一般四边形,所以直接求AD比较困难,应设法将AD转化为特殊三角形的边.
例4题图 例5题图
【例5】 如图,凸八边形中,∠=∠,∠=∠,∠=∠,∠=∠,试证明:该凸八边形内任意一点到8条边的距离之和是一个定值.
(山东省竞赛试题)
解题思路:本例是一个几何定值证明问题,关键是将八边形问题转化为三角形或四边形问题来解决,若连结对角线,则会破坏一些已知条件,应当考虑向外补形.
【例6】 如图,在△ABC中,∠ABC=,点D在边BC上,∠ADC=,且.将△ACD以直线AD为轴作轴对称变换,得到△,连结.
(1) 证明:⊥;
(2) 求∠C的大小.
(全国初中数学竞赛天津赛区初赛试题)
解题思路:本题分别考查了等边三角形的性质与判定、全等三角形的性质与判定及轴对称的性质,解题的关键是利用角平分线的性质与判定构造全等三角形,然后利用全等三角形的性质即可解决问题.
能力训练
1.如图,在四边形ABCD中,∠A=∠C=,AB=AD,若这个四边形的面积为12,则BC+CD=_____________. (山东省竞赛试题)
2. 如图,凸五边形ABCDE中,∠A=∠B=,EA=AB=BC=,CD=DE=,则这个五边形的面积为_______________.
(美国AHSME试题)
3. 如图,一个凸六边形六个内角都是,其中连续四条边的长依次为,则该六边形的周长为______________.
4. 如图,ABCDEF是正六边形,M,N分别是边CD,DE的中点,线段AM与BN相交于P,则
=_________. (浙江省竞赛试题)
5. 如图,长为的三条线段交于O点,并且∠=∠=∠=,则三个三角形的面积和__________(填“<”,“=”,或“>”).
(“希望杯”邀请赛试题)
6. 如图,在四边形ABCD中,∠A=,∠B=∠D=,BC=,CD=,则AB= ( ).
A. B. C. D.
(广西壮族自治区中考试题)
- 如图,在△ABC中,M为BC中点,AN平分∠A,AN⊥BN于N,且AB=,AC=,则MN等于( ).
A. B. C. D.
8. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=,BE⊥AD于E,,则BE的长为( )
A. B. C. D.
9. 如图,在四边形ABCD中,AB=,BC=,CD=,∠B=,∠C=,则∠D等于( )
A. B. C. D.条件不够,无法求出
(重庆市竞赛试题)
10. 如图,在△ABC中,E是AC中点,D是BC边上一点,若BC=,∠ABC=,∠BAC=,∠CED=,求的值.
11. 如图,设是的斜边长,是直角边,求证:.
(加拿大中学生竞赛试题)
12. 如图,已知八边形ABCDEFGH所有的内角都相等,而且边长都是整数.求证:这个八边形的对边相等.
13. 如图,设P为△ABC的中位线DE上的一点,BP交AC于N,CP交AB于M,求证:.
(齐齐哈尔市竞赛试题)
14. 一个圆内接八边形相邻的四条边长是,另四条边长是,求八边形的面积.
八年级数学 培优竞赛 专题18 直角三角形 讲义学案: 这是一份八年级数学 培优竞赛 专题18 直角三角形 讲义学案,文件包含八年级数学培优竞赛专题18直角三角形_答案doc、八年级数学培优竞赛专题18直角三角形讲义doc等2份学案配套教学资源,其中学案共31页, 欢迎下载使用。
八年级数学 培优竞赛 专题15 全等三角形 讲义学案: 这是一份八年级数学 培优竞赛 专题15 全等三角形 讲义学案,文件包含八年级数学培优竞赛专题15全等三角形讲义doc、八年级数学培优竞赛专题15全等三角形_答案doc等2份学案配套教学资源,其中学案共12页, 欢迎下载使用。
八年级数学 培优竞赛 专题14 多边形的边与角 讲义学案: 这是一份八年级数学 培优竞赛 专题14 多边形的边与角 讲义学案,文件包含八年级数学培优竞赛专题14多边形的边与角讲义doc、八年级数学培优竞赛专题14多边形的边与角_答案docx等2份学案配套教学资源,其中学案共8页, 欢迎下载使用。












