2017年七年级（下）巴蜀数学期末标准模拟试题

这是一份2017年七年级（下）巴蜀数学期末标准模拟试题，共35页。试卷主要包含了个棋子等内容，欢迎下载使用。
2017年七年级（下）巴蜀数学期末标准模拟试题（学生版）
满分 150分 测试时间 120分钟
一．选择题（共12小题，满分48分，每小题4分）
1．（4分）在以下回收、绿色食品、节能、节水四个标志中，是轴对称图形的是（　　）
A． B． C． D．
2．（4分）下列事件中，必然事件是（　　）
A．任意掷一枚均匀的硬币，正面朝上
B．打开电视正在播放甲型H1N1流感的相关知识
C．某射击运动员射击一次，命中靶心
D．在只装有5个红球的袋中摸出1球，是红球
3．（4分）在下列实数：、、、、﹣1.010010001…中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个

4．（4分）如图，已知∠1=∠2，其中能判定AB∥CD的是（　　）
A． B． C． D．

5．（4分）如图，已知CD⊥AB于D，现有四个条件：①AD=ED；②∠A=∠BED；③∠C=∠B；④AC=EB，那么不能得出△ADC≌△EDB的条件是（　　）

A．①③ B．②④ C．①④ D．②③

6．（4分）的平方根是（　　）
A．2 B．4 C．﹣2或2 D．﹣4或4

7．（4分）已知直角三角形的周长是2+，斜边长为 2，则它的面积是（　　）
A． B．1 C． D．

8．（4分）从分别标有数﹣3，﹣2，﹣1，1，2，3的六张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数均大于﹣2的概率是（　　）
A． B． C． D．

9．（4分）如图，△ABC中∠A=56°，PD垂直平分AB，PE垂直平分BC，则∠BPC的度数为（　　）


A．124° B．112° C．108° D．118°

10．（4分）下列图形是由同样大小的棋子按照一定规律排列而成的，其中，图1中有5个棋子，图2中有10个棋子，图3中有16个棋子，…，则图7中有（　　）个棋子．


A．35 B．40 C．45 D．50

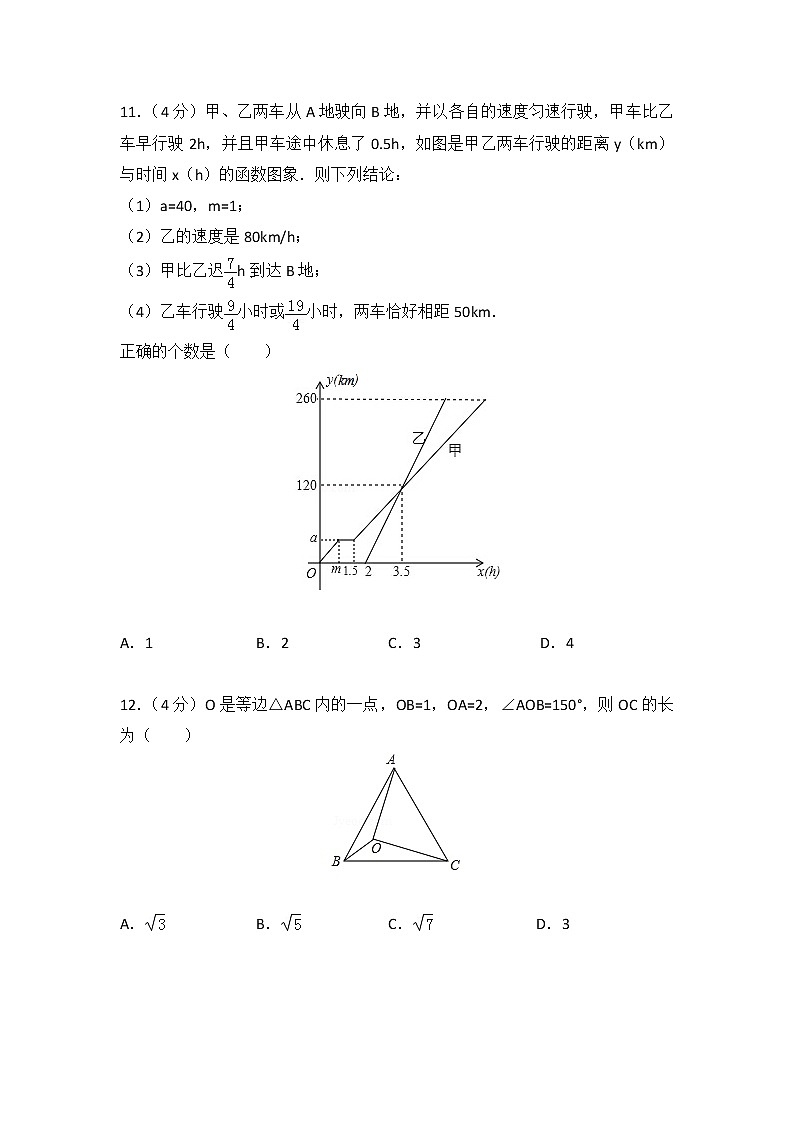
11．（4分）甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：
（1）a=40，m=1；
（2）乙的速度是80km/h；
（3）甲比乙迟h到达B地；
（4）乙车行驶小时或小时，两车恰好相距50km．
正确的个数是（　　）


A．1 B．2 C．3 D．4

12．（4分）O是等边△ABC内的一点，OB=1，OA=2，∠AOB=150°，则OC的长为（　　）


A． B． C． D．3
　

二．填空题（共10小题，满分30分，每小题3分）
13．（3分）若在实数范围内有意义，则x的取值范围是　　．

14．（3分）如图，把一张长方形纸条ABCD沿EF折叠，若∠1=50°，则∠AEG=　　．


15．（3分）如图，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP=　　．


16．（3分）如图，已知△ABC的两条高BD、CE交于点F，∠ABC的平分线与△ABC外角∠ACM的平分线交于点G，若∠BFC=8∠G，则∠A=　　°．

17．（3分）已知△ABC中，AB=AC，AB的垂直平分线交AB于点D，交直线AC于点E，若∠EBC=42°，则∠BAC的度数为　　．

18．（3分）一只小鸟自由自在在空中飞翔，然后随意落在下图（由16个小正方形组成）中，则落在阴影部分的概率是　　．

19．（3分）甲、乙两人在一条直线道路上分别从相距1500米的A，B 两点同时出发，相向而行，当两人相遇后，甲继续向点B前进（甲到达点B时停止运动），乙也立即向B点返回．在整个运动过程中，甲、乙均保持匀速运动．甲、乙两人之间的距离y（米）与乙运动的时间x（秒） 之间的关系如图所示．则甲到B点时，乙距B点的距离是　　米．


20．（3分）如图，长方体的长为15cm，宽为10cm，高为20cm，点B离点C为2cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是　　．


21．（3分）如图，已知△ABC的面积为8cm2，BP为∠ABC的角平分线，AP垂直BP于点P，则△PBC的面积为　　cm2．


22．（3分）如图，∠AOB=30°，点M，N分别在边OA，OB上，OM=，ON=3，点P，Q分别在边OB，OA上运动，连接MP，PQ，QN，则MP+PQ+QN的最小值为　　．

　
三．解答题（共7小题，满分72分）
23．（15分）计算：
（1）（﹣2）3+（7﹣π）0﹣（）﹣1；





（2）（﹣a2）3+（2a）2•a4；





（3）（x+2）2﹣（x+1）（x﹣1）．







24．（8分）化简求值：（m+n）2﹣2（m﹣n）（m+n）+（n﹣m）2，其中m=20，n=﹣2．










25．（7分）已知：如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC．
求证：BC=DE．










26．（10分）甲车从A地出发，途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从C地出发到B地后又按原速返回C地，两车同时出发，并以各自的速度匀速行驶，设A，C，B在同一条直线上，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
（1）直接写出m，n的值；
（2）分别求出甲、乙两车从C地到B地时y（千米）与x（小时）的函数关系式（写出自变量x的取值范围）；
（3）当两车相距60千米时，乙车行驶了多长时间．














27．（10分）如图，等腰直角三角形ABC中，∠BAC=90°，D、E分别为AB、AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．
（1）求证：△EGM为等腰三角形；
（2）判断线段BG、AF与FG的数量关系并证明你的结论．





















28．（10分）若将一个自然数从左到右各数位上的数字排列成一列后，后一个数减去前一个数的差始终是同一个常数，则这个自然数叫做“阶梯数”．如：四位数1357排列后为：1，3，5，7，因为7﹣5=5﹣3=3﹣1=2，且差2是常数，故1357是一个四位阶梯数．又如，9876，55555等数也是阶梯数．
若一个自然数从左到右各数位上的数字和另一个自然数从右到左各数位上的数字完全相同，则称这两个自然数互为逆序数，简称“互逆数”．例如：1357与7531，9876与6789，…，都是互逆数．
（1）写出任意一个三位阶梯数及其互逆数：　　、　　．并证明任意一个三位数与其互逆数的差能被198整除（设百位数为a，后一个数位于前一个数位差的常数为b，1≤a≤9，0≤b≤4，且a、b为整数）．
（2）若一个四位阶梯数能被6整除，求出符合条件的所有四位阶梯数．


















29．（12分）如图1，已知△ABC和△EFC都是等边三角形，点E在线段AB上．
（1）求证：AE=BF，BF∥AC；
（2）若点D在直线AC上，且ED=EC（如图2），求证：AB=AD+BF；
（3）在（2）的条件下，若点E改为在线段AB的延长线上，其它条件不变（如图3），请直接写出AB、AD、BF之间的数量关系．

　

2017年七年级（下）数学期末标准模拟试题（教师版）
一．选择题（共12小题，满分48分，每小题4分）
1．（4分）（2017•北市区一模）在以下回收、绿色食品、节能、节水四个标志中，是轴对称图形的是（　　）
A． B． C． D．
【解答】解：A、不是轴对称图形，故本选项错误；
B、是轴对称图形，故本选项正确；
C、不是轴对称图形，故本选项错误；
D、不是轴对称图形，故本选项错误．
故选；B．
　
2．（4分）（2017•峄城区模拟）下列事件中，必然事件是（　　）
A．任意掷一枚均匀的硬币，正面朝上
B．打开电视正在播放甲型H1N1流感的相关知识
C．某射击运动员射击一次，命中靶心
D．在只装有5个红球的袋中摸出1球，是红球
【解答】解：A、任意掷一枚均匀的硬币，可能正面朝上，也可能反面朝上，是随机事件；
B、打开电视，可能正在播放甲型H1N1流感的相关知识，也可能正在播放其它内容，是随机事件；
C、某射击运动员射击一次，可能命中靶心，也可能脱靶，是随机事件；
D、在只装有5个红球的袋中摸出1球，是红球，是必然事件．
故选D．
　
3．（4分）（2017•沭阳县一模）在下列实数：、、、、﹣1.010010001…中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
【解答】解：、、﹣1.010010001…是无理数，
故选：C．
　
4．（4分）（2017春•路北区期中）如图，已知∠1=∠2，其中能判定AB∥CD的是（　　）
A． B． C． D．
【解答】解：A、∵∠1=∠2，
∴AD∥BC（内错角相等，两直线平行）；
B、∵∠1=∠2，∠1、∠2不是同位角和内错角，
∴不能得出两直线平行；
C、∠1=∠2，∠1、∠2不是同位角和内错角，
∴不能得出两直线平行；
D、∵∠1=∠2，
∴AB∥CD（同位角相等，两直线平行）．
故选D．
　
5．（4分）（2017春•宝丰县校级月考）如图，已知CD⊥AB于D，现有四个条件：①AD=ED；②∠A=∠BED；③∠C=∠B；④AC=EB，那么不能得出△ADC≌△EDB的条件是（　　）

A．①③ B．②④ C．①④ D．②③
【解答】解：A、∵CD⊥AB，
∴∠ADC=∠BDE=90°，
在△ADC和△EDB中，
∵，
∴△ADC≌△EDB（AAS），正确，故本选项错误；
B、∵CD⊥AB，
∴∠ADC=∠BDE=90°，
在△ADC和△EDB中，
∵，
∴△ADC≌△EDB（AAS），正确，故本选项错误；
C、∵CD⊥AB，
∴∠ADC=∠BDE=90°，
在Rt△ADC和Rt△EDB中，
∵，
∴Rt△ADC≌Rt△EDB（HL），正确，故本选项错误；
D、根据三个角对应相等，不能判断两三角形全等，错误，故本选项正确；
故选D．
　
6．（4分）（2017春•防城港期中）的平方根是（　　）
A．2 B．4 C．﹣2或2 D．﹣4或4
【解答】解：∵，
∴的平方根是±2，
故选C．
　
7．（4分）（2017春•襄城区校级月考）已知直角三角形的周长是2+，斜边长为 2，则它的面积是（　　）
A． B．1 C． D．
【解答】解：设直角三角形的两直角边为a、b，
则a+b+2=2+，a2+b2=22=4，
∴a+b=，（a+b）2﹣2ab=4，
解得：ab=1，
∴这个直角三角形的面积为ab=，
故选：A．
　
8．（4分）（2017•徐水县模拟）从分别标有数﹣3，﹣2，﹣1，1，2，3的六张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数均大于﹣2的概率是（　　）
A． B． C． D．
【解答】解：∵﹣3，﹣2，﹣1，1，2，3的六张卡片中，大于﹣2的有﹣1，1，2，3这4张，
∴所抽卡片上的数大于﹣2的概率是=，
故选：D．
　
9．（4分）如图，△ABC中∠A=56°，PD垂直平分AB，PE垂直平分BC，则∠BPC的度数为（　　）

A．124° B．112° C．108° D．118°
【解答】解：如图，连接PA，∵PD垂直平分AB，PE垂直平分BC，
∴PA=PB，PB=PC，
∴PA=PB=PC，
∴∠PBA=∠PAB，∠PCA=∠PAC，
∵∠A=56°，
∴∠PBA+∠PCA=∠PAB+∠PAC=∠A=56°，
在△ABC中，∠PBC+∠PCB=180°﹣∠A﹣（∠PBA+∠PCA）=180°﹣56°﹣56°=68°，
在△PBC中，∠BPC=180°﹣（∠PBC+∠PCB）=180°﹣68°=112°．
故选B．

　
10．（4分）（2017•江北区一模）下列图形是由同样大小的棋子按照一定规律排列而成的，其中，图1中有5个棋子，图2中有10个棋子，图3中有16个棋子，…，则图7中有（　　）个棋子．

A．35 B．40 C．45 D．50
【解答】解：∵图1中棋子有5=1+2+1×2个，
图2中棋子有10=1+2+3+2×2个，
图3中棋子有16=1+2+3+4+3×2个，
…
∴图7中棋子有1+2+3+4+5+6+7+8+7×2=50个，
故选：D．
　
11．（4分）（2016•黄冈模拟）甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：
（1）a=40，m=1；
（2）乙的速度是80km/h；
（3）甲比乙迟h到达B地；
（4）乙车行驶小时或小时，两车恰好相距50km．
正确的个数是（　　）

A．1 B．2 C．3 D．4
【解答】解：（1）由题意，得m=1.5﹣0.5=1．
120÷（3.5﹣0.5）=40（km/h），则a=40，故（1）正确；
（2）120÷（3.5﹣2）=80km/h（千米/小时），故（2）正确；
（3）设甲车休息之后行驶路程y（km）与时间x（h）的函数关系式为y=kx+b，由题意，得

解得：
∴y=40x﹣20，
根据图形得知：甲、乙两车中先到达B地的是乙车，
把y=260代入y=40x﹣20得，x=7，
∵乙车的行驶速度：80km/h，
∴乙车的行驶260km需要260÷80=3.25h，
∴7﹣（2+3.25）=h，
∴甲比乙迟h到达B地，故（3）正确；
（4）当1.5＜x≤7时，y=40x﹣20．
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b'，由题意得

解得：
∴y=80x﹣160．
当40x﹣20﹣50=80x﹣160时，
解得：x=．
当40x﹣20+50=80x﹣160时，
解得：x=．
∴﹣2=，﹣2=．
所以乙车行驶小时或小时，两车恰好相距50km，故（4）错误．
故选（C）
　
12．（4分）（2016秋•江夏区期中）O是等边△ABC内的一点，OB=1，OA=2，∠AOB=150°，则OC的长为（　　）

A． B． C． D．3
【解答】解：如图，将△AOB绕B点顺时针旋转60°到△BO′C的位置，由旋转的性质，得BO=BO′，
∴△BO′O为等边三角形，
由旋转的性质可知∠BO′C=∠AOB=150°，
∴∠CO′O=150°﹣60°=90°，
又∵OO′=OB=1，CO′=AO=2，
∴在Rt△COO′中，由勾股定理，得OC===．
故选B．

　
二．填空题（共10小题，满分30分，每小题3分）
13．（3分）（2017•新区一模）若在实数范围内有意义，则x的取值范围是　x≥2　．
【解答】解：∵在实数范围内有意义，
∴3x﹣6≥0，解得x≥2，
∴x的取值范围为x≥2．
故答案为：x≥2．
　
14．（3分）（2017•武汉模拟）如图，把一张长方形纸条ABCD沿EF折叠，若∠1=50°，则∠AEG=　80°　．

【解答】解：∵四边形ABCD是长方形，
∴AD∥BC，
∴∠DEF=∠1=50°，
∵沿EF折叠D到D′，
∴∠FEG=∠DEF=50°，
∴∠AEG=180°﹣50°﹣50°=80°，
故答案为：80°．
　
15．（3分）（2011•随州）如图，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP=　50°　．

【解答】解：延长BA，作PN⊥BD，PF⊥BA，PM⊥AC，
设∠PCD=x°，
∵CP平分∠ACD，
∴∠ACP=∠PCD=x°，PM=PN，
∵BP平分∠ABC，
∴∠ABP=∠PBC，PF=PN，
∴PF=PM，
∵∠BPC=40°，
∴∠ABP=∠PBC=∠PCD﹣∠BPC=（x﹣40）°，
∴∠BAC=∠ACD﹣∠ABC=2x°﹣（x°﹣40°）﹣（x°﹣40°）=80°，
∴∠CAF=100°，
在Rt△PFA和Rt△PMA中，
∵，
∴Rt△PFA≌Rt△PMA（HL），
∴∠FAP=∠PAC=50°．
故答案为：50°．

　
16．（3分）（2016春•常州期末）如图，已知△ABC的两条高BD、CE交于点F，∠ABC的平分线与△ABC外角∠ACM的平分线交于点G，若∠BFC=8∠G，则∠A=　36　°．

【解答】解：由三角形的外角性质得，∠ACM=∠A+∠ABC，∠GCM=∠G+∠GBC，
∵∠ABC的平分线与∠ACM的平分线交于点G，
∴∠GBC=∠ABC，∠GCM=∠ACD，
∴∠G+∠GBC=（∠A+∠ABC）=∠A+∠GBC，
∴∠G=∠A，
∵∠BFC=8∠G，且BD⊥AC，CE⊥AB，
∴∠BFC+∠A=180°，
∴8∠G+∠A=180°，
∴5∠A=180°，
∴∠A=36°，
故答案为36．
　
17．（3分）（2017•萧山区模拟）已知△ABC中，AB=AC，AB的垂直平分线交AB于点D，交直线AC于点E，若∠EBC=42°，则∠BAC的度数为　32°或152°或88°　．
【解答】解：如图1，∵△ABC是等腰三角形，
∴∠ABC=∠ACB，∠ABC+∠ACB+∠A=180°，
∵DE垂直且平分AB，
∴EA=EB，
∴∠ABE=∠A，
∴∠EBC+∠ACB=∠AEB，
42°+（180°﹣∠A）=180°﹣2∠A，
解得∠BAC=32°．
如图2，同理可得∠BAC=152°，
如图3，同理可得∠BAC=88°，
综上所述∠BAC=32°或152°或88°，
故答案为：32°或152°或88°．



　
18．（3分）（2015春•宣汉县期末）一只小鸟自由自在在空中飞翔，然后随意落在下图（由16个小正方形组成）中，则落在阴影部分的概率是　　．

【解答】解：设每个小正方形的边长为1，
由图可知：阴影部分面积为：×1×3﹣×1×2+（×3×4﹣×3×3）+（×3×4﹣×3×2）==5
所以图中阴影部分占5个小正方形，其面积占总面积的，
所以其概率为．
故答案为：．
　
19．（3分）（2017•南岸区一模）甲、乙两人在一条直线道路上分别从相距1500米的A，B 两点同时出发，相向而行，当两人相遇后，甲继续向点B前进（甲到达点B时停止运动），乙也立即向B点返回．在整个运动过程中，甲、乙均保持匀速运动．甲、乙两人之间的距离y（米）与乙运动的时间x（秒） 之间的关系如图所示．则甲到B点时，乙距B点的距离是　87.5　米．

【解答】解：由题可得，甲从A到达B运动的时间为375秒，
∴甲的速度为：1500÷375=4m/s，
又∵甲乙两人从出发到相遇的时间为200秒，
∴乙的速度为：1500÷200﹣4=3.5m/s，
又∵甲从相遇的地点到达B的路程为：175×4=700米，
乙在两人相遇后运动175秒的路程为：175×3.5=612.5米，
∴甲到B点时，乙距B点的距离为：700﹣612.5=87.5米，
故答案为：87.5
　
20．（3分）（2016春•鄂城区月考）如图，长方体的长为15cm，宽为10cm，高为20cm，点B离点C为2cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是　4cm　．

【解答】解：把右侧面展开到水平面上，连结AB，如图1，AB===2（cm）；
把右侧面展开到正面上，连结AB，如图2，AB===4（cm）；
把向上的面展开到正面上，连结AB，如图3，AB===2（cm）．
所以一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离为4cm．
故答案为4cm．

　
21．（3分）（2015春•深圳校级期中）如图，已知△ABC的面积为8cm2，BP为∠ABC的角平分线，AP垂直BP于点P，则△PBC的面积为　4　cm2．

【解答】解：延长AP交BC于E，
∵AP垂直∠B的平分线BP于P，
∠ABP=∠EBP，
又知BP=BP，∠APB=∠BPE=90°，
在△ABP与△BEP中，

∴△ABP≌△BEP（ASA），
∴S△ABP=S△BEP，AP=PE，
∴△APC和△CPE等底同高，
∴S△APC=S△PCE，
设△ACE的面积为m，
∴S△ABE=S△ABC+S△ACE=10+m
∴S△PBC=S△ABE﹣S△ACE=﹣=4cm2．
故答案为：4．

　
22．（3分）（2017•江西模拟）如图，∠AOB=30°，点M，N分别在边OA，OB上，OM=，ON=3，点P，Q分别在边OB，OA上运动，连接MP，PQ，QN，则MP+PQ+QN的最小值为　5　．

【解答】解：作M关于OB的对称点M′，作N关于OA的对称点N′，
连接M′N′，即为MP+PQ+QN的最小值．
根据轴对称的定义可知：∠N′OQ=∠M′OB=30°，∠ONN′=60°，
∴△ONN′为等边三角形，△OMM′为等边三角形，
∴∠N′OM′=90°，
∴在Rt△M′ON′中，
M′N′==5．
故答案为5．

　
三．解答题（共7小题，满分72分）
23．（15分）（2017春•泰兴市期中）计算：
（1）（﹣2）3+（7﹣π）0﹣（）﹣1；
（2）（﹣a2）3+（2a）2•a4；
（3）（x+2）2﹣（x+1）（x﹣1）．
【解答】解：（1）原式=﹣8+1﹣3=﹣10；
（2）原式=﹣a6+4a6=3a6；
（3）原式=x2+4x+4﹣x2+1=4x+5．
　
24．（8分）（2015春•东台市校级月考）化简求值：（m+n）2﹣2（m﹣n）（m+n）+（n﹣m）2，其中m=20，n=﹣2．
【解答】解：（m+n）2﹣2（m﹣n）（m+n）+（n﹣m）2
=m2+2mn+n2﹣2m2+2n2+n2﹣2mn+m2
=4n2，
当n=﹣2时，原式=4×（﹣2）2=16．
　
25．（7分）（2016•句容市一模）已知：如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC．
求证：BC=DE．

【解答】证明：∵AB∥EC，
∴∠A=∠DCE，
在△ABC和△CDE中，，
∴△ABC≌△CDE，
∴BC=DE．
　
26．（10分）甲车从A地出发，途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从C地出发到B地后又按原速返回C地，两车同时出发，并以各自的速度匀速行驶，设A，C，B在同一条直线上，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
（1）直接写出m，n的值；
（2）分别求出甲、乙两车从C地到B地时y（千米）与x（小时）的函数关系式（写出自变量x的取值范围）；
（3）当两车相距60千米时，乙车行驶了多长时间．

【解答】解：（1）∵甲车途经C地时休息一小时，
∴2.5﹣m=1，
∴m=1.5，
甲车的速度==120，
n=2.5+=2.5+1=3.5
所以m=1.5，n=3.5；

（2）设甲车从C地到B地时的y与x的函数关系式为y=kx+b（k≠0），
因为函数图象经过（2.5，120）和（3.5，0），
所以，，
解得 ，
所以，y=﹣120x+420（2.5≤x≤3.5）．
设乙车从C地到B地时的y与x的函数关系式为y=k′x+b′（k′≠0），
因为函数图象经过（0，120）和（2，0），
所以，，
解得 ，
所以，y=﹣60x+120（0≤x≤2）．

（3）设两车相距60千米时，乙车行驶了x小时，
乙车的速度为：120÷2=60千米/时，
①若相遇前，则120（x﹣2.5）+60（x﹣2）=120﹣60，
解得x=，
②若相遇后，则120（x﹣2.5）+60（x﹣2）=120+60，
解得x=．
所以，两车相距60千米时，乙车行驶了小时或小时．
　
27．（10分）（2009秋•西城区期末）如图，等腰直角三角形ABC中，∠BAC=90°，D、E分别为AB、AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．
（1）求证：△EGM为等腰三角形；
（2）判断线段BG、AF与FG的数量关系并证明你的结论．

【解答】（1）证明：∵等腰直角三角形ABC中，∠BAC=90°，
∴AC=AB，∠ACB=∠ABC=45°，
又∵AD=AE，∠CAD=∠BAE，
∴△ACD≌△ABE（SAS），
∴∠1=∠3，
∵∠BAC=90°，
∴∠3+∠2=90°，∠1+∠4=90°，
∴∠4+∠3=90°
∵FG⊥CD，
∴∠CMF+∠4=90°，
∴∠3=∠CMF，
∴∠GEM=∠GME，
∴EG=MG，△EGM为等腰三角形．

（2）答：线段BG、AF与FG的数量关系为BG=AF+FG．
证明：过点B作AB的垂线，交GF的延长线于点N．（见右图）
∵BN⊥AB，∠ABC=45°，
∴∠FBN=45°=∠FBA．
∵FG⊥CD，
∴∠BFN=∠CFM=90°﹣∠DCB，
∵AF⊥BE，
∴∠BFA=90°﹣∠EBC，∠5+∠2=90°，
由（1）可得∠DCB=∠EBC，
∴∠BFN=∠BFA，
又∵BF=BF，
∴△BFN≌△BFA（ASA），
∴NF=AF，∠N=∠5，
又∵∠GBN+∠2=90°，
∴∠GBN=∠5=∠N，
∴BG=NG，
又∵NG=NF+FG，
∴BG=AF+FG．

　
28．（10分）若将一个自然数从左到右各数位上的数字排列成一列后，后一个数减去前一个数的差始终是同一个常数，则这个自然数叫做“阶梯数”．如：四位数1357排列后为：1，3，5，7，因为7﹣5=5﹣3=3﹣1=2，且差2是常数，故1357是一个四位阶梯数．又如，9876，55555等数也是阶梯数．
若一个自然数从左到右各数位上的数字和另一个自然数从右到左各数位上的数字完全相同，则称这两个自然数互为逆序数，简称“互逆数”．例如：1357与7531，9876与6789，…，都是互逆数．
（1）写出任意一个三位阶梯数及其互逆数：　123　、　123和321　．并证明任意一个三位数与其互逆数的差能被198整除（设百位数为a，后一个数位于前一个数位差的常数为b，1≤a≤9，0≤b≤4，且a、b为整数）．
（2）若一个四位阶梯数能被6整除，求出符合条件的所有四位阶梯数．
【解答】解：（1）三位阶梯数为：123，互逆数为：123和321，
根据题意得：百位数为a，则十位数字为：a+b，个位数字为：a+2b，
其互逆数的百位数为a+2b，则十位数字为：a+b，个位数字为：a，
则100a+10（a+b）+（a+2b）﹣[100（a+2b）+10（a+b）+a]，
=100a+10a+10b+a+2b﹣100a﹣200b﹣10a﹣10b﹣a，
=﹣198b，
∴任意一个三位数与其互逆数的差能被198整除；
故答案为：123，123或321；
（2）设这个四位阶梯数的首位数字为a，差是b（1≤a≤9，|b|≤3，且a、b为整数），
①当b=0时，这四位数字都是a，则1000a+100a+10a+a=1111a，
当a=6时，这个四位阶梯数为6666，能被6整除；
②当b=1时，这四位数字分别是a、a+1、a+2、a+3，则1000a+100（a+1）+10（a+2）+a+3=1111a+123，
当a=3时，这个四位阶梯数为3456，能被6整除；
③当b=2时，这四位数字分别是a、a+2、a+4、a+6，则1000a+100（a+2）+10（a+4）+a+6=1111a+246，
此时没有能被6整除的四位阶梯数；
④当b=3时，这四位数字分别是a、a+3、a+6、a+9，则1000a+100（a+3）+10（a+6）+a+9=1111a+369，
此时没有能被6整除的四位阶梯数；
⑤当b=﹣1时，这四位数字分别是a、a﹣1、a﹣2、a﹣3，则1000a+100（a﹣1）+10（a﹣2）+a﹣3=1111a﹣123，
当a=3时，这个四位阶梯数为3210，能被6整除；
当a=9时，这个四位阶梯数为9876，能被6整除；
⑥当b=﹣2时，这四位数字分别是a、a﹣2、a﹣4、a﹣6，则1000a+100（a﹣2）+10（a﹣4）+a﹣6=1111a﹣246，
当a=6时，这个四位阶梯数为6420，能被6整除；
⑦当b=﹣3时，这四位数字分别是a、a﹣3、a﹣6、a﹣9，则1000a+100（a﹣3）+10（a﹣6）+a﹣9=1111a﹣369，
当a=9时，这个四位阶梯数为9630，能被6整除；
综上所述，符合条件的所有四位阶梯数分别是：6666、3456、3210、9876、6420、9630．
　
29．（12分）（2016秋•孝南区期末）如图1，已知△ABC和△EFC都是等边三角形，点E在线段AB上．
（1）求证：AE=BF，BF∥AC；
（2）若点D在直线AC上，且ED=EC（如图2），求证：AB=AD+BF；
（3）在（2）的条件下，若点E改为在线段AB的延长线上，其它条件不变（如图3），请直接写出AB、AD、BF之间的数量关系．

【解答】解：（1）如图1，∵△ABC和△EFC都是等边三角形，
∴∠ACB=∠ECF=60°，AC=BC，CE=FC，
∴∠1=∠2，
在△ACE和△BCF中，
，
∴△ACE≌△BCF（SAS），
∴AE=BF，且∠BAC=∠FBC=60°，
又∠ABC=60°，
∴∠A+∠ABC+∠FBC=180°，即∠A+∠ABF=180°，
∴AC∥BF；

（2）证明：如图2，过E作EM∥BC交AC于M，
∵∠ABC=∠ACB=60°，
∴∠AEM=∠AME=60°，
∴△AEM是等边三角形，
∴AE=EM=AM，
∴∠DAE=∠EMC=120°，
∵DE=CE，
∴∠D=∠1，
在△ADE和△MCE中，
，
∴△ADE≌△MCE（AAS），
∴AD=CM，
由（1）得△ACE≌△FCB，
∴BF=AE=AM，
∵AC=AM+CM，
∴AC=BF+AD，
即AB=BF+AD；

（3）AB、AD、BF之间的数量关系为：AB=BF﹣AD，
理由：如图3，过E作EM∥BC交AC的延长线于M，
∵∠ABC=∠ACB=60°，
∴∠AEM=∠AME=60°，
∴△AEM是等边三角形，
∴AE=EM=AM，
∴∠DAE=∠EMC=60°，
∵DE=CE，
∴∠ADE=∠DCE，
∴∠ADE=∠ECM，
在△ADE与△MCE中，
，
∴△ADE≌△MCE（AAS），
∴AD=CM，
由（1）得△ACE≌△FCB，
∴BF=AE=AM，
∵AM=AC+CM，
∴AC=AM﹣CM，
∴AC=BF﹣AD，
即AB=BF﹣AD．