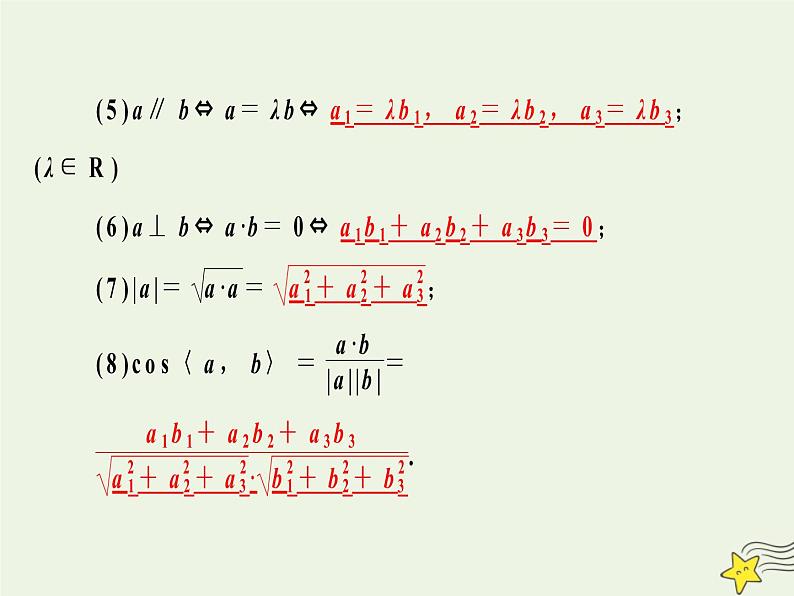
2021学年3.1空间向量及其运算授课ppt课件

这是一份2021学年3.1空间向量及其运算授课ppt课件，共51页。PPT课件主要包含了预习自测，答案A，变式训练，课堂小结等内容，欢迎下载使用。

1.掌握空间向量的坐标运算．2．会根据向量的坐标，判断两个向量共线或垂直．3．掌握向量长度，两向量夹角和两点间距离公式.
2．与向量a＝(1,2,3)，b＝(3,1,2)都垂直的向量为(　　)A．(1,7,5) B．(1，－7,5)C．(－1，－7,5) D．(1，－7，－5)解析：利用数量积为零逐一验证可求得．答案：C
解析：向量的共线和平行是一样的，可利用空间向量共线定理写成数乘的形式，即b≠0，a∥b⇔a＝λb，观察选项，只有C符合．答案：C
4．若a＝(2,3，－1)，b＝(－2,1,3)，则以a，b为邻边的平行四边形的面积为________．
类型一　　空间向量的坐标运算[例1]　已知O为坐标原点，A、B、C三点的坐标分别是(2，－1,2)、(4,5，－1)、(－2,2,3)，求点P的坐标，使
[点评]　向量的坐标即终点坐标减去起点的对应坐标．反之求点的坐标时，一定要注意向量的起点是否在原点．在原点时，向量的坐标与原坐标相同．不在原点时，向量的坐标加上起点坐标才是终点坐标．
已知向量a＝(1，－2,4)，求同时满足以下三个条件的向量x：①a·x＝0；②|x|＝10；③x与向量b＝(1,0,0)垂直．
类型二　　坐标形式下的平行与垂直[例2]　(1)已知向量a＝(2,4,5)，b＝(3，x，y)，若a∥b，求x、y的值．(2)已知：a＝(2,4，x)，b＝(2，y,2)，若|a|＝6，且a⊥b，求x＋y的值．[分析]　(1)∵a∥b，∴a＝λb，λ一定存在，故可设λ.(2)a⊥b，∴a·b＝0，再加上条件|a|＝6，可求x、y的值．
类型三　　坐标形式下的夹角与距离
类型四　　利用空间向量的坐标运算解决立体几何问题
[点评]　从上述解法来看，向量的坐标及运算为解决线段长度及两线垂直方面的问题提供了有力的、方便的工具，以后遇到几何体中的夹角、距离、垂直、平行问题时，要善于将其转化为向量间的夹角、模、垂直、平行问题，利用向量方法解决．
加法、减法和数量积同平面向量类似，具有类似的运算法则，学习中可类比推广．但能不能推广是难点所在，应抓住空间向量的坐标表示这一根本去突破，即向量a在平面上是用唯一确定的有序实数对表示，即a＝(x，y)，在空间也是这样定义的．不同点仅是向量在不同空间具有不同的表达形式，
空间两向量平行同平面两向量平行的表达式不一样，但实质是一致的，即对应坐标成比例，且比值为λ.空间两向量垂直同平面两向量垂直公式类似．向量长度公式是表示向量的长度，其形式与平面向量长度公式一致，学习时可用类比的方法进行．它的几何意义是表示长方体对角线的长度．