专题02 半角模型-2022年中考数学几何模型解题策略（课件 讲义）

这是一份专题02 半角模型-2022年中考数学几何模型解题策略（课件 讲义），文件包含专题02半角模型pptx、专题02半角模型解析版doc、专题02半角模型原卷版doc等3份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。
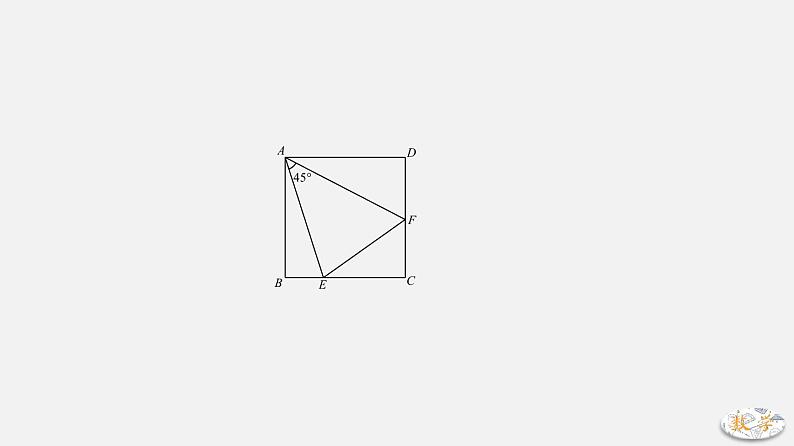
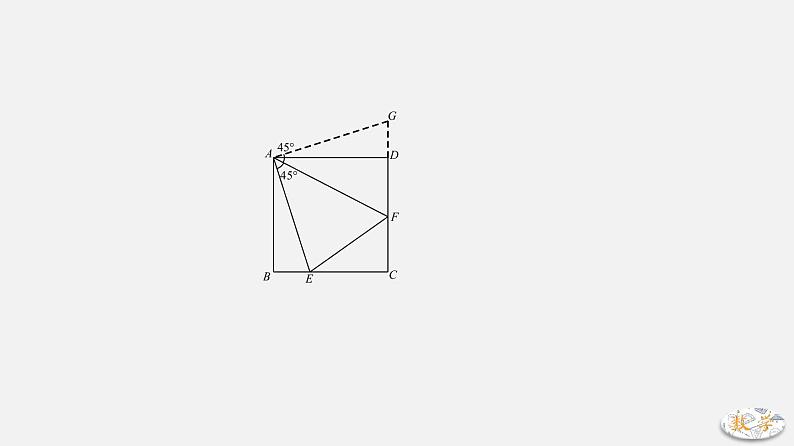
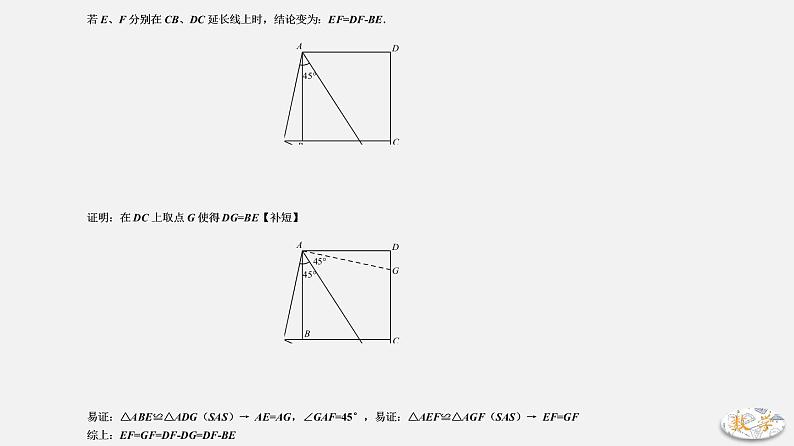
专题02 半角模型一、方法突破1．90°+45°模型．如图，在正方形ABCD中，E、F分别在BC、CD上，且∠EAF=45°连接EF．【两个基本结论】结论1：EF=BE+DF．证明：延长CD至点G使得DG=BE【截长】易证：△ABE≌△ADG（SAS）→ AE=AG，∠GAF=45°易证：△AFE≌△AFG（SAS）→ EF=GF综上：EF=GF=GD+DF=BE+DF．若E、F分别在CB、DC延长线上时，结论变为：EF=DF-BE．
证明：在DC上取点G使得DG=BE【补短】易证：△ABE≌△ADG（SAS）→ AE=AG，∠GAF=45°易证：△AEF≌△AGF（SAS）→ EF=GF综上：EF=GF=DF-DG=DF-BE【小结】截长、补短只是形式，关键点在于已知半角的情况下，构造相应的另一个半角．此处通过旋转，想要将一个图形毫无违和地旋转到另一位置，需要：邻边相等，对角互补．正方形可满足一切你所想． 结论2：连接BD，与AE、AF分别交于M、N，则：．证明：构造△ADM’≌△ABM → AM=AM’，∠MAN=∠M’AN，BM=DM’易证：△AMN≌△AM’N（SAS）→ MN=M’N易证：△M’DN是直角三角形 → → ．
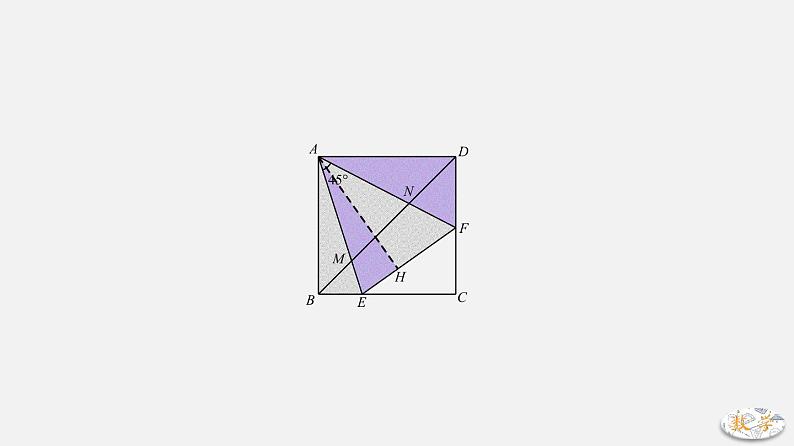
【其他结论】结论3：若，则点F是CD边中点．反之亦然．结论4：过点A作AH⊥EF交EF于H点，则△ABE≌△AHE，△AHF≌△ADF．另外还可得：AE平分∠BEF，AF平分∠DFE．结论5：A、B、E、N四点共圆，A、D、F、M四点共圆．证明：∠EAN=∠EBN=45°，∴A、B、E、N四点共圆．同理可证A、D、F、M四点共圆．另外还可得：连接EN、MF，可得△AEN、△AMF是等腰直角三角形．结论6：M、N、F、E四点共圆．证明：∵∠MEF=∠MFN，∴M、N、F、E四点共圆．结论7：△AMN∽△AFE．且．由构图3可得∠ANM=∠AEF，∠AMN=∠AFE．可得△AMN∽△AFE．结论8：△MAN∽△MDA，△NAM∽△NBA．结论9：连接AC，则△AMB∽△AFC，△AND∽△AEC．且．【思考】对于以上9个结论，在正方形中，有哪些作为条件能推出∠EAF=45°的？【小结】从结论5开始，后面的可能都用不上，但既然半角模型作为题型出现，了解下图形的更多性质有时候能帮上大忙．在这里除了给的∠EAF=45°外，正方形对角线也会形成其他45°角，多组相等角总能撞出些火花．
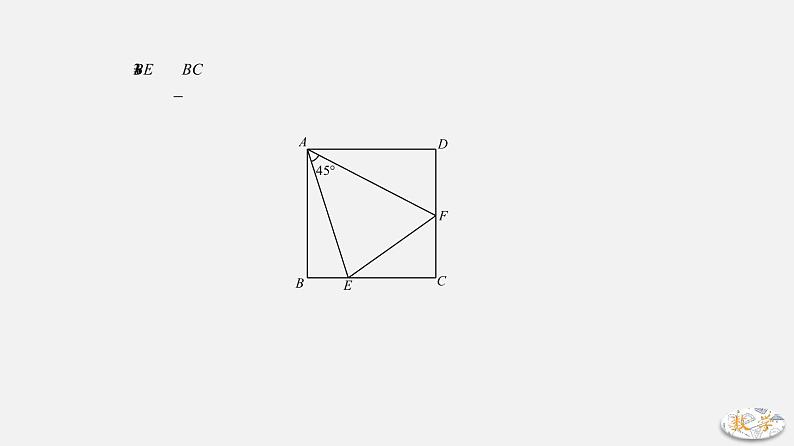
2．120°+60°模型（1）如图，△ABC是等边三角形，BD=CD且∠BDC=120°，E、F在直线AB、AC上且∠EDF=60°结论：EF=BE+CF证明：延长AC至点G使得CG=BE， 易证：△DBE≌△DCG（SAS）→ DE=DG，∠FDG=∠FDE=60°易证：△DFE≌△DFG（SAS）→ EF=GF综上：EF=GF=GC+CF=BE+CF （2）若点F在AC的延长线上，EF、BE、CF之间又有何数量关系？二、典例精析例一：如图，正方形的边长为2，点，分别在边，上，若，则的周长等于　　．【分析】半角模型．根据半角模型结论可知EF=AE+CF，∴△EDF的周长等于DA+DC=4，故△EDF的周长为4． 例二：已知如图，在正方形中，，，分别是，上的一点，且，，将绕点沿顺时针方向旋转后与重合，连接，过点作，交于点，则以下结论：①，②，③，④中正确的是　　A．①②③ B．②③④ C．①③④ D．①②④【分析】半角模型结论①显然正确；设BF=x，则EF=3+x，CF=4-x，勾股定理得：，解得：，故结论②正确；，故结论③错误；∵BM∥AG，∴△FBM∽△FGA，且，，∴，故结论④正确；综上所述，选D．例三：如图，已知正方形ABCD的边长为a，E为CD边上一点（不与端点重合），将△ADE沿AE对折至△AFE，延长EF交 边BC于点G，连接AG，CF．给出下列判断：①∠EAG=45°；②若，则AG∥CF；③若E为CD的中点，则△GFC的面积为；④若CF=FG，则；⑤．其中正确的是______．（写出所有正确判断的序号） 【分析】半角模型．结论①正确，易证△ADE≌△AFE，△AFG≌△ABG，∴．结论②正确，若，则G是BC中点，GC=GF，∴∠GCF=∠GFC，又∠CFG+∠GFC=∠FGB，∴∠GFC=∠FGA，∴AG∥CF．结论③错误，∠FGB=2∠FGA，∴∠FGC=∠FGA，∴AG∥CF．若E为CD中点，则，，有，∴．结论④正确，若GF=FC，则DE=BG，不妨设DE=BG=x，则GE=2x，，由△ECG是等腰直角三角形，可得：，解得：．结论⑤正确，正方形面积是，是五边形ABGED的面积，故证明△GEC面积为即可．设BG=m，DE=n，则EG=m+n，CG=a-m，CE=a-n，根据勾股定理可得：，化简得：，∴．综上所述，正确的是①②④⑤． 三、中考真题演练1．如图，正方形中，、分别在边、上，且，连接，这种模型属于“半角模型”中的一类，在解决“半角模型”问题时，旋转是一种常用的分析思路．例如图中与可以看作绕点旋转的关系．这可以证明结论“”，请补充辅助线的作法，并写出证明过程．（1）延长到点，使　　，连接；（2）证明：．【解答】解：（1）与可以看作绕点旋转的关系．延长到点，使，连接，故答案为：；（2）证明：由（1）得，，，，，，四边形为正方形，，，，，在和中，，，，，．2．半角模型是指有公共顶点，锐角等于较大角的一半，且组成这个较大角的两边相等．通过翻折或旋转，将角的倍分关系转化为角的相等关系，并进一步构成全等或相似三角形，弱化条件，变更载体，而构建模型，可把握问题的本质．（1）问题背景：如图1，在四边形中，，，，、分别是、上的点，且．探究图中线段，，之间的数量关系；（2）探索延伸：如图2，若在四边形中，，．、分别是、上的点，且，上述结论是否仍然成立，并说明理由；（3）结论应用：如图3，在某次军事演习中，舰艇甲在指挥中心处）北偏西的处，舰艇乙在指挥中心南偏东的处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里小时的速度前进，舰艇乙沿北偏东的方向以80海里小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达、处，且两舰艇与指挥中心之间的夹角，试求此时两舰艇之间的距离；（4）能力提高：如图，等腰直角三角形中，，，点、在边上，且，若，，试求出的长．【解答】解：（1）如图1，，理由如下：在和中，，，，，，，，在和中，，，，，；（2）如图2，（1）中的结论仍然成立，即．理由：延长到点．使．连接，在和中，，，，，，，，在和中，，，，，；（3）如图3，连接，延长、相交于点，，，，，，符合探索延伸中的条件，结论成立，即（海里）．此时两舰艇之间的距离为210海里．（4）能力提高如图4，作，使，连接，，是等腰直角三角形，，，，，，在和中，，，，，，在和中，，，，在中，，．3．小明、小亮在共同学习的过程中经常会遇到一类几何问题：两个角度是一半关系，并且这两个角共顶点，他们称之“半角问题”；常见的半角模型是含，含．问题背景：（1）如图1，在正方形中，、分别是、边上的点，且，探究图中线段，，之间的数量关系．小明的探究思路是：延长到，使，连接，先证明，再证明．小亮发现这里可以由经过一种图形变换得到，请你写出这种变换的过程 　可以由绕点逆时针旋转得到　．（不需要证明）拓展研究：（2）如图2，在四边形中，，，、分别是边、上的点，且，试问线段、、具有怎样的数量关系？写出证明过程．（3）如图3，在四边形中，，与互补，点、分别在射线、上，且．当，，时，的周长等于 　　．【解答】解：（1）从图形看，可以由绕点逆时针旋转得到，故答案为：可以由绕点逆时针旋转得到； （2）结论：，理由是：如图2，延长到，使，连接．，，，在与中，，，，，．．又，，．．； （3）在上截取，，，，，，；，，；是与的公共边，，；，．的周长，故答案为：13．4．已知，如图1，四边形是正方形，、分别在边、上，且，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法．（1）在图1中，连接，为了证明结论“”，小明将绕点顺时针旋转后解答了这个问题，请按小明的思路写出证明过程；（2）如图2，当的两边分别与、的延长线交于点、，连接，试探究线段、、之间的数量关系，并证明．【解答】（1）证明：由旋转可得，，，四边形为正方形，，，，，在和中，，，；（2）解：，证明如下：如图，把绕点逆时针旋转到，交于点，同（1）可证得，，且，．5．【模型引入】当几何图形中，两个共顶点的角存在角度是公共大角一半的关系，我们称之为“半角模型”．【模型探究】（1）如图1，在正方形中，、分别是、边上的点，且，探究图中线段，，之间的数量关系．【模型应用】（2）如图2，如果四边形中，，，，且，，，求的长．【拓展提高】（3）如图3，在四边形中，，与互补，点、分别在射线、上，且．当，，时，的周长等于 　13　．（4）如图4，正方形中，的顶点、分别在、边上，，且，连接分别交、于点，若，，，求、的长．（5）如图5，在菱形中，，点、分别是边、上的动点（不与端点重合），且，连接分别与边、交于、，当时，求证：．【解答】解：（1）绕点逆时针旋转，得到，，，，，，，、、三点共线，在和中，，，，； （2）解：如图3中，在上取一点，使得，，，，，，，，，，，，，，，，，，设，则，，在中，，，，； （3）在上截取，，，，，，；，，，是与的公共边，，；，．的周长，故答案为：13； （4）先证明一个结论，如图，已知中，，，点、在斜边上，且，则，证明：是等腰直角三角形，，逆时针旋转至，，，，，连接，根据勾股定理得，，，，，，，，，；四边形是正方形，，，，，在和中，，，，，同理可证，，，，，．设正方形的边长为，，，根据勾股定理得，，（舍或，，，由（1）可知，，，由上述结论得：，设，，．，，解得，，；（5）将绕顺时针旋转，此时与重合，转到，在上取，连接、，如图：绕顺时针旋转得，，又，，，，，，，即，而，，，，，菱形，，，，，，中，，，，，，．6．如图1：在四边形中，，，，、分别是，上的点，且，探究图中线段，，之间的数量关系．小王同学探究此问题的方法是：延长到点，使，连接，先证明，再证明，即可得出，，之间的数量关系，他的结论应是　　．像上面这样有公共顶点，锐角等于较大角的一半，且组成这个较大角的两边相等的几何模型称为半角模型．拓展如图2，若在四边形中，，，、分别是，上的点，且，则，，之间的数量关系是　　．请证明你的结论．实际应用如图3，在某次军事演习中，舰艇甲在指挥中心处）北偏西的处，舰艇乙在指挥中心南偏东的处，且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以60海里小时的速度前进，舰艇乙沿北偏东的方向以80海里小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达，处，且两舰艇之间的夹角为，试求此时两舰艇之间的距离是　　海里（直接写出答案）．【解答】解：如图1，，理由如下：在和中，，，，，，，，在和中，，，，，；故答案为；如图2，，理由：延长到点．使．连接，在和中，，，，，，，，在和中，，，，，；如图3，连接，延长、相交于点，，，，，，符合探索延伸中的条件，结论成立，即（海里）．故答案为：168．7．已知如图1，四边形是正方形，，分别在边、上，且，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法．（1）在图1中，连接，为了证明结论“ “，小亮将绕点顺时针旋转后解答了这个问题，请按小亮的思路写出证明过程；（2）如图2，当绕点旋转到图2位置时，试探究与、之间有怎样的数量关系？（3）如图3，如果四边形中，，，，且，，，求的长．【解答】（1）证明：如图1中，由旋转可得，，，四边形为正方形，，，，，在和中，，，，，． （2）解：结论：，理由：如图2中，把绕点逆时针旋转到，交于点，同（1）可证得，，且，． （3）解：如图3中，在上取一点，使得，，，，，，，，，，，，，，，，，，设，则，，在中，，，，．