专题01 有关等腰三角形、等边三角形和直角三角形的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

专题1 有关等腰三角形、等边三角形和直角三角形的常见压轴题

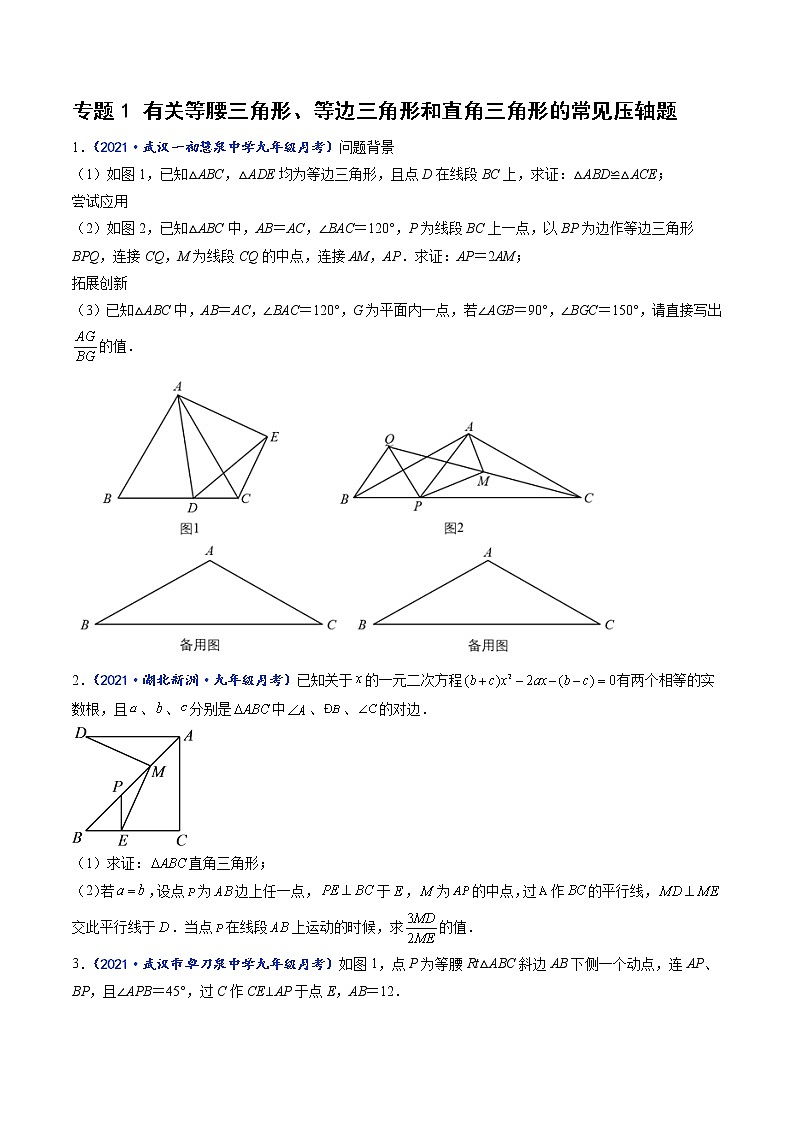
1．（2021·武汉一初慧泉中学九年级月考）问题背景

（1）如图1，已知△ABC，△ADE均为等边三角形，且点D在线段BC上，求证：△ABD≌△ACE；

尝试应用

（2）如图2，已知△ABC中，AB＝AC，∠BAC＝120°，P为线段BC上一点，以BP为边作等边三角形BPQ，连接CQ，M为线段CQ的中点，连接AM，AP．求证：AP＝2AM；

拓展创新

（3）已知△ABC中，AB＝AC，∠BAC＝120°，G为平面内一点，若∠AGB＝90°，∠BGC＝150°，请直接写出的值．

2．（2021·湖北新洲·九年级月考）已知关于的一元二次方程有两个相等的实数根，且、、分别是中、、的对边．

（1）求证：直角三角形；

（2）若，设点为边上任一点，于，为的中点，过作的平行线，交此平行线于．当点在线段上运动的时候，求的值．

3．（2021·武汉市卓刀泉中学九年级月考）如图1，点P为等腰Rt△ABC斜边AB下侧一个动点，连AP、BP，且∠APB＝45°，过C作CE⊥AP于点E，AB＝12．

（1）若∠ACE＝15°，求△ABP的面积；

（2）求的值；

（3）如图2，当△APC为等腰三角形时，则其面积为 　 　．

4．（2021·重庆十八中两江实验中学九年级月考）已知：在△ABC中，∠ABC=90°，点D为直线BC上一点，连接AD并延长，过点C作AC的垂线交AD的延长线于点E．

（1）如图1，若∠BAC=60°，CE=AC，AB=1，求线段AE的长度；

（2）如图2，若AC=EC，点F是线段BA延长线上一点，连接EF与BC交于点H，且∠BAD=∠ACF，求证：AF=2BH；

（3）如图3，AB=2，BC=6，点M为AE中点，连接BM，CM，当|CM-BM|最大时，直接写出△BMC的面积．

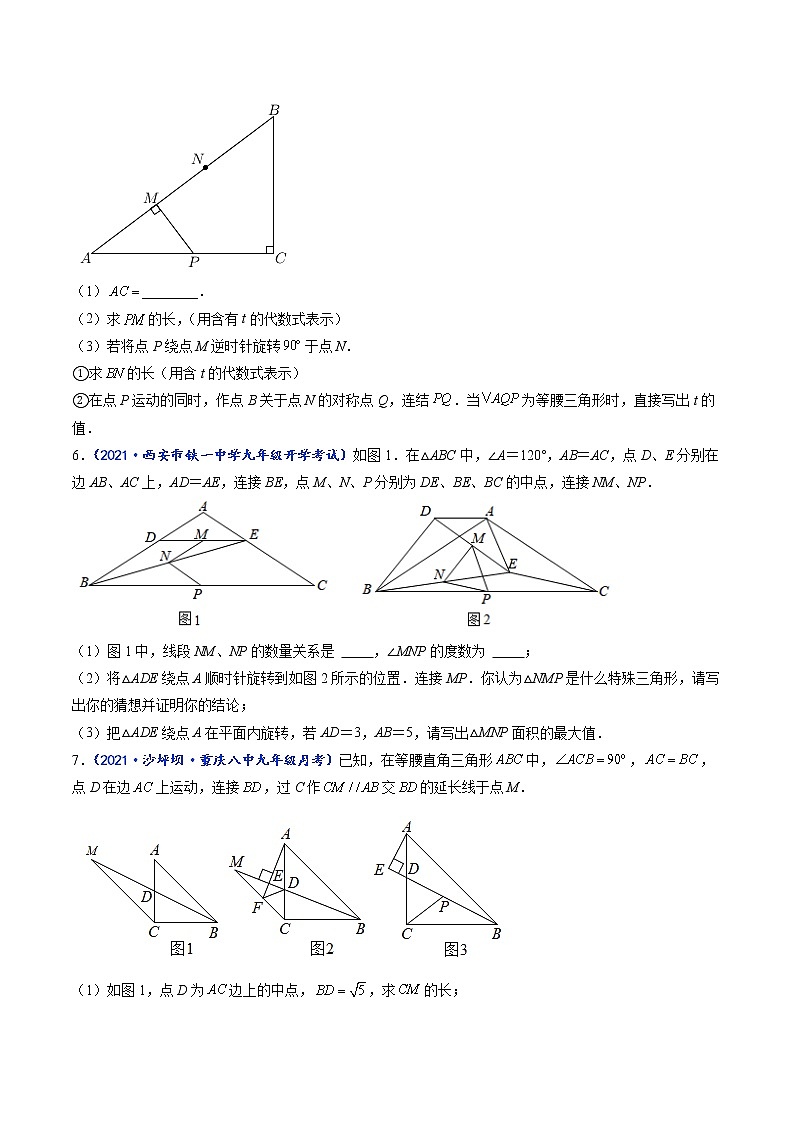
5．（2021·吉林省第二实验学校九年级月考）如图，在中，，，，动点P从点A出发，沿以每秒5个单位长度的速度向终点C匀速运动，设点P的运动时间为t秒（），过点P作的垂线交于点M．

（1）________．

（2）求的长，（用含有t的代数式表示）

（3）若将点P绕点M逆时针旋转于点N．

①求的长（用含t的代数式表示）

②在点P运动的同时，作点B关于点N的对称点Q，连结．当为等腰三角形时，直接写出t的值．

6．（2021·西安市铁一中学九年级开学考试）如图1．在△ABC中，∠A＝120°，AB＝AC，点D、E分别在边AB、AC上，AD＝AE，连接BE，点M、N、P分别为DE、BE、BC的中点，连接NM、NP．

（1）图1中，线段NM、NP的数量关系是 　 　，∠MNP的度数为 　 　；

（2）将△ADE绕点A顺时针旋转到如图2所示的位置．连接MP．你认为△NMP是什么特殊三角形，请写出你的猜想并证明你的结论；

（3）把△ADE绕点A在平面内旋转，若AD＝3，AB＝5，请写出△MNP面积的最大值．

7．（2021·沙坪坝·重庆八中九年级月考）已知，在等腰直角三角形中，，，点D在边上运动，连接，过C作交的延长线于点M．

（1）如图1，点D为边上的中点，，求的长；

（2）如图2，过点A作于点E，交于点F，连接，求证：；

（3）如图3，过点A作交的延长线于点E，P为的中点，，请直接写出的最小值．

8．（2021·诸暨市开放双语实验学校九年级期中）（1）问题发现

如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．

填空：①∠AEB的度数为　   　；

②线段AD，BE之间的数量关系为　   　．

（2）拓展探究

如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

（3）解决问题

如图3，在正方形ABCD中，CD＝，若点P满足PD＝1，且∠BPD＝90°，请直接写出点A到BP的距离．

9．（2021·重庆字水中学九年级三模）如图，在等边中，AD是BC边上的高，点E为线段AD上一点，连EB、EC．

（1）如图1，将线段EB绕点E顺时针旋转至EF，使点F落在BA的延长线上．

①求的度数；

②求证：；

（2）如图2，若，将线段EB绕点E旋转过程中与边AC交于点H，当时，请直接写出的最小值．

10．（2021·吉林省第二实验学校九年级月考）已知Rt△ABC中，∠CAB＝90°，AB＝4，AC=3，点 P 从点 B 处出发，以每秒2个单位长度的速度沿 B﹣A﹣C，运动时间为 t 秒，以 AP 为斜边作等腰直角三角形 PQA，点Q始终在点A的右上方，

（1）用t表示线段AP的长．

（2）点Q落在线段BC上时，求t的值．

（3）点P在线段AB上运动时，点A'是点A关于直线QP的对称点，当点A'与△ACB的顶点所连线段平行△ACB的一条直角边时，求△ABC与重叠部分的面积S的值．

（4）点 E 是线段 AC 中点，当直线 QE 把△ABC 的面积分为 2：3 两部分时，直接写出 t 的值．

11．（2021·长春市第二实验中学九年级月考）如图，在Rt△ABC中，∠C＝90°，BC＝4cm，AC＝8cm，点P从点A出发，沿AC方向以2cm/s的速度向终点C运动，PD⊥AC，PD＝PA，点F在射线AC上，FP＝2PA，以PD、PF为邻边构造矩形PDEF，设点P的运动时间为t（s）．

（1）AF＝　　（用含t的代数式表示）．

（2）当点B落在DE上时，求t的值．

（3）连接BF，△ABF是等腰三角形时，求t的值．

（4）当点E在△ABC的边的垂直平分线上时，直接写出t的值．

12．（2021·南师附中树人学校九年级月考）如图1，若△DEF的三个顶点D，E，F分别在△ABC各边上，则称△DEF是△ABC的内接三角形．

（1）如图2，点D，E，F分别是等边三角形ABC各边上的点，且AD＝BE＝CF，则△DEF是△ABC的内接 　 　．

A．等腰三角形  B．等边三角形

C．等腰三角形或等边三角形 D．直角三角形

（2）如图3，已知等边三角形ABC，请作出△ABC的边长最小的内接等边三角形DEF．（保留作图痕迹，不写作法）

（3）问题：如图4，△ABC是不等边三角形，点D在AB边上，是否存在△ABC的内接等边三角形DEF？如果存在，如何作出这个等边三角形？

①探究1：如图5，要使△DEF是等边三角形，只需∠EDF＝60°，DE＝DF．于是，我们以点D为角的顶点任作∠EDF＝60°，且DE交BC于点E，DF交AC于点F．

我们选定两个特殊位置考虑：位置1（如图6）中的点F与点C重合，位置2（如图7）中的点E与点C重合．在点E由位置1中的位置运动到位置2中点C的过程中，DE逐渐变大而DF逐渐变小后再变大，如果存在某个时刻正好DE＝DF，那么这个等边三角形DEF就存在（如图8）．理由：　 　是等边三角形．

②探究2：在BC上任取点E，作等边三角形DEF（如图9），并分别作出点E与点B、点C重合时的等边三角形DBF′和DCF″．连接FF'，FF″，证明：FF'+FF″＝BC．

③探究3：请根据以上的探究解决问题：如图10，△ABC是不等边三角形，点D在AB边上，请作出△ABC的内接等边三角形DEF．（保留作图痕迹，不写作法）

13．（2021·合肥实验学校九年级二模）等腰直角△AOB和等腰直角△COD按如图方式放置，∠AOB＝∠COD＝90°，连接AC、BD，二者交于点P．

（1）求证：BD＝AC；

（2）连接OP，若OP平分∠AOD，且角∠AOD＝40°，求∠BDO的度数；

（3）点M、N分别是AB、CD的中点，连接MN，求的值．

14．（2021·湖南郴州·中考真题）如图1，在等腰直角三角形中，．点，分别为，的中点，为线段上一动点（不与点，重合），将线段绕点逆时针方向旋转得到，连接，．

（1）证明：；

（2）如图2，连接，，交于点．

①证明：在点的运动过程中，总有；

②若，当的长度为多少时，为等腰三角形？

15．（2021·河南安阳·九年级一模）在中，，，将边绕点A逆时针旋转至，记旋转角为．分别过A，C作直线的垂线，垂足分别是E，F，连接交直线于点Q．

（1）如图1，当时，的形状为____________；

（2）当时，

①（1）中的结论是否成立？如果成立，请就图2的情形进行证明；如果不成立，请说明理由；

②在旋转过程中，当线段时，请直接写出的长．