专题02 有关四边形的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

这是一份专题02 有关四边形的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1，文件包含专题02有关四边形的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题02有关四边形的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。

专题2 有关四边形的常见压轴题
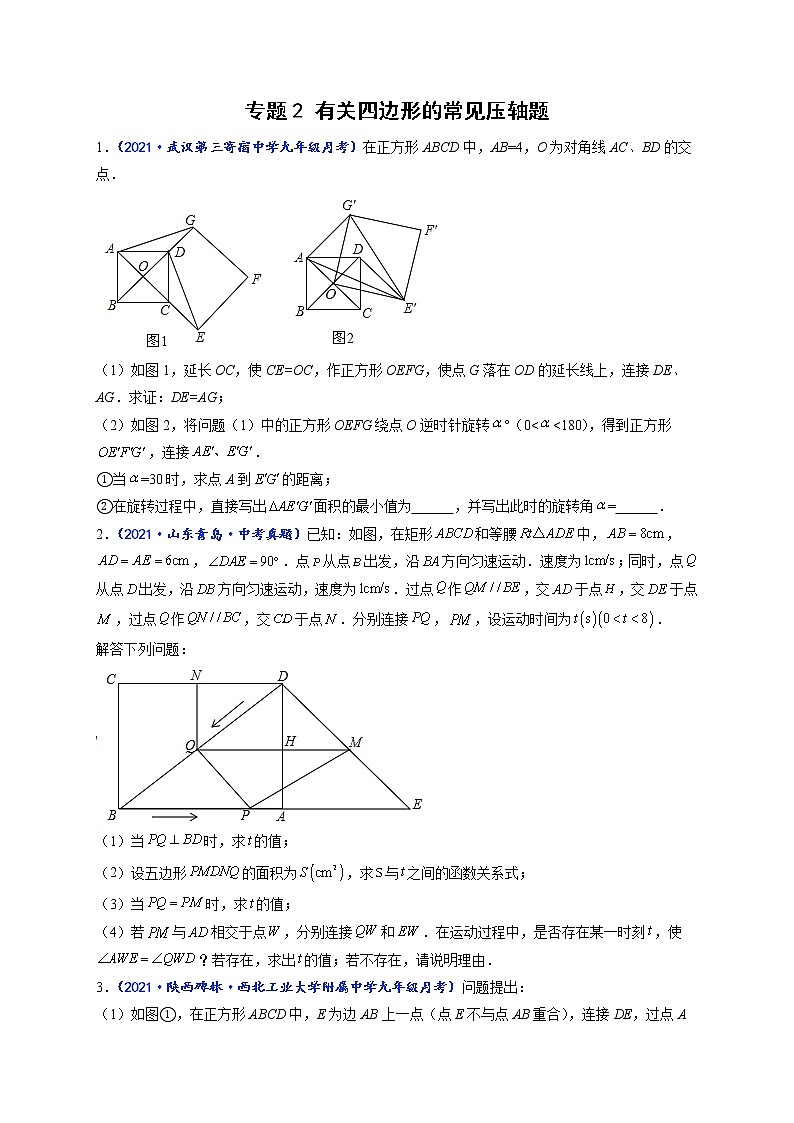
1．（2021·武汉第三寄宿中学九年级月考）在正方形ABCD中，AB=4，O为对角线AC、BD的交点．

（1）如图1，延长OC，使CE=OC，作正方形OEFG，使点G落在OD的延长线上，连接DE、AG．求证：DE=AG；
（2）如图2，将问题（1）中的正方形OEFG绕点O逆时针旋转°（0<<180），得到正方形，连接．
①当=30时，求点A到的距离；
②在旋转过程中，直接写出面积的最小值为 ，并写出此时的旋转角= ．
【答案】（1）见解析；（2）①点A到的距离为；②在旋转过程中，直接写出面积的最小值为，此时的旋转角=135°．
【解题思路分析】（1）证明△AOG≌△DOE得出AG=DE即可；
（2）① 过点E′作E′M⊥AC交AC延长线于点M，过点A作AN⊥G′E′于点N，则∠E′MO=90°,求出OG′=OE′=， 可得出G′E′=8,则可得出答案；
②可知G′，E′在以O为圆心，OG′为半径的圆O上，当OA⊥G′E′时，S△AE′G′最小，此时OA的延长线与G′E′相交于点H，进一步即可得出答案．
【解析】(1)证明：∵点O是正方形ABCD两对角线的交点，
∴OA=OD.
∵OA⊥OD，
∴∠AOG=∠DOE=90°.
∵四边形OEFG是正方形，
∴OG=OE，
∴△AOG≌△DOE，
∴AG=DE.
(2)解：如图，过点E′作E′M⊥AC交AC延长线于点M，过点A作AN⊥G′E′于点N，

则∠E′MO=90° .
∵在正方形ABCD中，
∴OA=OC=AB= .
∵正方形OEFG绕着O点逆时针旋转α(0<α<180)得到正方形OE′F′G′，
∴∠MOE′=∠DOG′=α=30°，∠G′OE′=90°
∴∠OE′M=90°−∠MOE′=60°.
又∠AOG′=∠AOD−α=60°，
∴∠AOG′=∠OE′M，OE′=OE=2OC= ，
∴OG′=OE′=，
∴G′E′==8，
∴ME′=OE′==OA，
∴△AOG′≌△ME′O，
∴∠OAG′=∠M=90°，
∴AG′=OA⋅tan∠AOG′= ，
∴AM=OA+OM=+.
∵AG′⋅AM=E′G′⋅AN，
∴AN==3+，
∴点A到E′G′的距离为3+.
②∵G′E′为定长，
∴G′，E′在以O为圆心，OG′为半径的圆O上，

∴当OA⊥G′E′时，S△AE′G′最小，
此时OA的延长线与G′E′相交于点H，
∴OH=G′E′=4，
∴AH=OH−AH=4-2 ，
∴S△AE′G′=E′G′⋅AH−16−8，
α=∠HOG′+∠AOD=45°+90°=135°．
2．（2021·山东青岛·中考真题）已知：如图，在矩形和等腰中，，，．点从点出发，沿方向匀速运动．速度为；同时，点从点出发，沿方向匀速运动，速度为．过点作，交于点，交于点，过点作，交于点．分别连接，，设运动时间为．
解答下列问题：

（1）当时，求的值；
（2）设五边形的面积为，求与之间的函数关系式；
（3）当时，求的值；
（4）若与相交于点，分别连接和．在运动过程中，是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由．
【答案】（1）；（2）；（3）；（4）存在，
【解题思路分析】（1）先证~，得代数计算即可；
（2）如图2中，过点P作PO⊥QM于点O．证明S=S四边形DQPM+S△DNQ=（PQ+DH）•QM+QN•ND=（HA+DH）•QM+QN•ND=•AD•QM+QN•ND，可得结论．
（3）如图3中，延长NQ交BE于点G．根据PQ=PM，构建方程求解即可．
（4）存在．证明△HQW∽△AEW，△MHW∽△PAW，推出，，推出，由此构建方程求解即可
【解析】（1）由题意可得，，，
在矩形中，
∵，，
，
在中，，
，
∴，
∵，
∴，
又∵，
∴~，
∴，
∴，
∴.
答：为时，.

（2）过点作，交于点，
在等腰中，
，，
则.
∵，
∴，
∴四边形是矩形，
∴.
∵，
∴，
又∵，
∴~，
∴，∴，∴.
∵，∴，
又∵，
∴~，
∴，
∴，
∴，.
∴




.
答：与的函数关系式是.

（3）延长交于点，由（1），（2）可得，
，，
∵，
∴四边形是矩形，
∴，
同理可证，四边形是矩形.
∴，
当时，
∵，
∴，
∴.
又∵，
∴，
∴.
答：当时，.

（4）由（2）得，，

∵，，
∴，
∴为矩形，
∴，且.
∴，
∵，
∴~，
同理可证~，
∴，，
∴，
∴，
∴.
答：在运动的过程中，存在时刻，使.
3．（2021·陕西碑林·西北工业大学附属中学九年级月考）问题提出：
（1）如图①，在正方形ABCD中，E为边AB上一点（点E不与点AB重合），连接DE，过点A作AF⊥DE，交BC于点F，则DE与AF的数量关系是：DE　 　AF；
问题探究：
（2）如图②，在矩形ABCD中，AB＝4，AD＝6，点E、F分别在边AB、CD上，点M为线段EF上一动点，过点M作EF的垂线分别交边AD、BC于点G、点H．若线段EF恰好平分矩形ABCD的面积，且DF＝1，求GH的长；
问题解决：
（3）如图③，在正方形ABCD中，M为AD上一点，且，E、F分别为BC、CD上的动点，且BE＝2DF，若AB＝4，求ME+2AF的最小值．


【答案】（1）见解析；（2）；（3）
【解题思路分析】（1）只需要证明△ADE≌△BAF即可得到答案；
（2）先根据EF平分矩形ABCD的面积，求出，过点F作FQ⊥AB于Q与GH交于O，过点G作GT⊥BC于T，与FQ交于点P则可得到AQ=DF=1，FQ=AD=6，GT=AB=4，∠GPQ=∠GPO=90°，再证明△QFE∽△TGH，得到即，再利用勾股定理求出EF的长即可得到答案；
（3）过点M作MH⊥BC于H，先证明四边形CDMH是矩形，得到MH=CD=4，CH=MD，然后求出MD=1 ，BH=BC-CH=3，设DF=x，则BE=2DF=2x，EH=BH-BE=3-2x，利用勾股定理得到，，则，最后利用平面直角坐标系的最小值等价于在x轴上找一点C使得AC+BC的值最小，由此利用两点距离公式进行求解即可．
【解析】解：（1）设AF与DE交点为O
∵四边形ABCD是正方形，
∴∠DAE=∠ABF=90°，AD=BA
∴∠DAO+∠BAF=90°，
∵AF⊥DE，
∴∠AOD=90°，
∴∠ADO+∠DAO=90°，
∴∠ADE=∠BAF，
∴△ADE≌△BAF（ASA），
∴DE=AF，
故答案为：=；


（2）∵四边形ABCD是矩形，
∴CD=AB=4，AD=BC=6，∠D=∠A=∠C=∠B=90°，CD∥AB，
∵EF平分矩形ABCD的面积，
∴，
∴，
如图，过点F作FQ⊥AB于Q与GH交于O，过点G作GT⊥BC于T，与FQ交于点P
∴四边形ADFQ，四边形ABTG是矩形，四边形AQPG是矩形，∠FQE=∠GTH=90°
∴AQ=DF=1，FQ=AD=6，GT=AB=4，∠GPQ=∠GPO=90°，
∵GH⊥EF，
∴∠FMO=∠GPO=90°，
又∵∠GOP=∠FOM，
∴∠QFE=∠TGH，
∴△QFE∽△TGH，
∴即，
∵，
∴，
∴；


（3）如图所示，过点M作MH⊥BC于H，
∴∠MHC=∠MHB=90°
∵四边形ABCD是正方形，
∴AD=BC=CD=4，∠B=∠BAD=∠D=∠C=90°，
∴四边形CDMH是矩形，
∴MH=CD=4，CH=MD，
∵，，
∴，
∴BH=BC-CH=3，
设DF=x，则BE=2DF=2x，
∴EH=BH-BE=3-2x，
∴，，
∴，


如下图所示，点A的坐标为（0，8），B（3，-4），C（2x，0），
∴，，
∴的最小值等价于在x轴上找一点C使得AC+BC的值最小，
∴当A、B、C三点共线时AC+BC的值最小
∴此时,
∴的最小值为．


4．（2021·成都嘉祥外国语学校九年级月考）综合与实践
问题情境：数学活动课上，老师出示了一个问题：如图①，在平行四边形ABCD中，BE⊥AD，垂足为E，F为CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明．

独立思考：（1）请解答老师提出的问题；
实践探究：（2）希望小组受此问题的启发，将平行四边形ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C′，连接DC′并延长交AB于点G，请判断AG与BG的数量关系，并加以证明．
问题解决：（3）智慧小组突发奇想，将▱ABCD沿过点B的直线折叠，如图③，点A的对应点为A′，使A′B⊥CD于点H，折痕交AD于点M，连接A′M，交CD于点N．该小组提出一个问题：若此平行四边形ABCD的面积为20，边长AB＝5，BC＝2，求图中阴影部分（四边形BHNM）的面积．请你思考此问题，直接写出结果．
【答案】（1）EF=BF，理由见解析； （2）AG=BG，理由见解析； （3） ．
【解题思路分析】（1）过点F作FH∥AD交BE于点H，可得FH垂直平分BE，即可求证；
（2）连接 ，根据折叠知识和等腰三角形的性质，可证得四边形DFBG是平行四边形，从而得到DF=BG，即可求证；
（3）过点D作DJ⊥AB于点J，过点M作MT⊥AB于点T，可先证得四边形DJBH是矩形，从而得到 ，再由相似三角形的性质，可得，从而得到 ，NH=2，再由，即可求解．
【解析】解：（1）结论：EF=BF，理由如下：
如图，过点F作FH∥AD交BE于点H，

∵四边形ABCD是平行四边形，
∴AD∥BC，
∵FH∥AD，
∴DE∥FH∥CB，
∵F为CD的中点，即DF=CF，
∴
∴EH=HB，
∵BE⊥AD，FH∥AD，
∴FH⊥EB，
∴EF=BF；
（2）结论：AG=BG，理由如下：
连接 ，


由折叠知识得： ， ，
∵DF=FC，
∴，
∴ ，
∴，
∴
∴ ，
∴DG∥BF，
∵DF∥BG，
∴四边形DFBG是平行四边形，
∴DF=BG，
∵ ，
∴ ，
∴AG=GB；
（3）如图，过点D作DJ⊥AB于点J，过点M作MT⊥AB于点T，

∵S平行四边形ABCD=AB×DJ，
∴DJ= ，
∵BC＝2，
∴ ，
在平行四边形ABCD中，AB∥CD，
∵ ，
∴ ，
∵DJ⊥AB，
∴∠DJB=∠JBH=∠DHB=90°，
∴四边形DJBH是矩形，
∴BH=DJ=4，
∴ ，
∵MT⊥AB，DJ⊥AB，
∴MT∥DJ，
∴ ~，
∴ ，
∴，
设AT=x，则MT=2x，
根据折叠得： ，
∴MT=TB=2x，
∴3x=5，解得： ，
∴ ，
∵ ，
∴~ ，
∴ ，
∴ ，
∴NH=2，
∴ ，
∴ ．
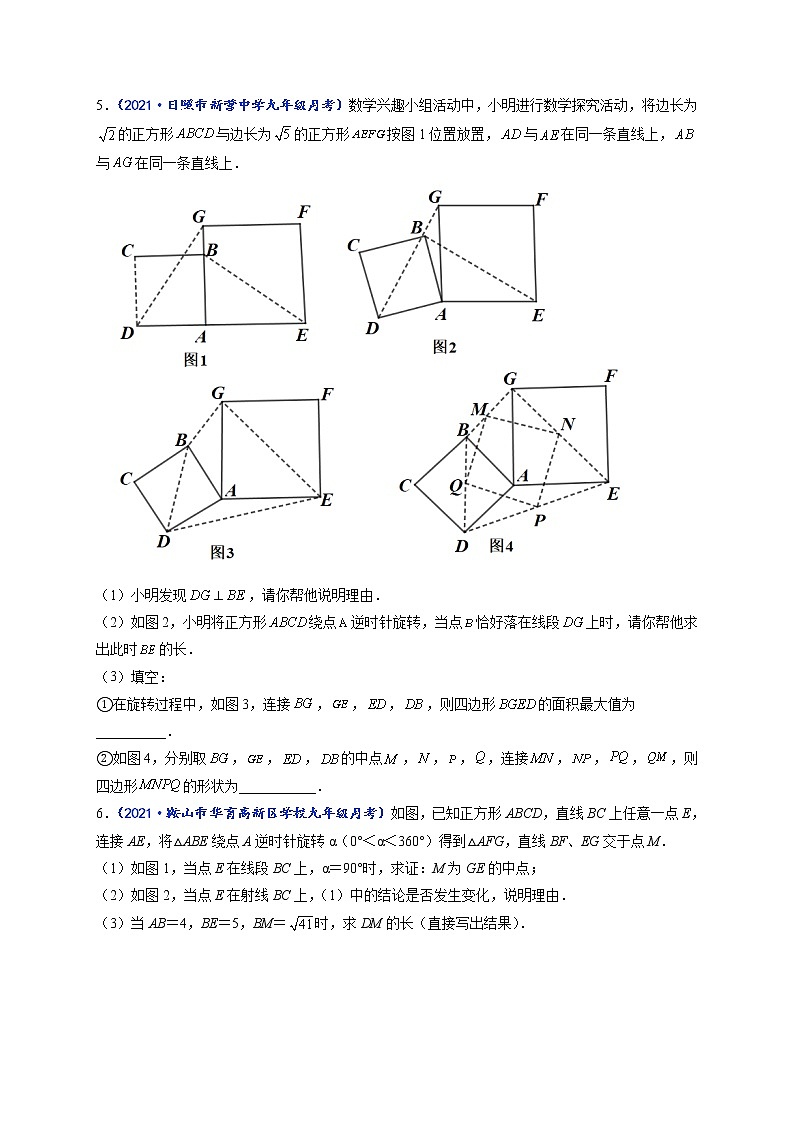
5．（2021·日照市新营中学九年级月考）数学兴趣小组活动中，小明进行数学探究活动，将边长为的正方形与边长为的正方形按图1位置放置，与在同一条直线上，与在同一条直线上．

（1）小明发现，请你帮他说明理由．
（2）如图2，小明将正方形绕点逆时针旋转，当点恰好落在线段上时，请你帮他求出此时的长．
（3）填空：
①在旋转过程中，如图3，连接，，，，则四边形的面积最大值为__________．
②如图4，分别取，，，的中点，，，，连接，，，，则四边形的形状为___________．
【答案】（1）证明见解析；（2）3；（3）①；②正方形，理由见解析
【解题思路分析】（1）由正方形的性质可证，因此可证得，延长交于点，然后由三角形的内角和和直角三角形的两锐角互余可证得结论；
（2）由正方形的性质和等量代换可证，因此可证得；过点作交于点，根据正方形的性质可证得，然后根据勾股定理可求得的长，进而可求得；
（3）①由（1）（2）可得：旋转过程中，始终有： 则· 所以当最大时，四边形的面积最大，即当三点共线时，面积最大，从而可得答案；②连接 同理可得：再利用三角形的中位线的性质证明即可得到结论.
【解析】解：（1）如图，延长交于

四边形与四边形是正方形，
，，
在和中，，
，
，
中，
，
中，，
，
；
（2）四边形与四边形是正方形，
，，，
，
，
在和中，，
，
，
如图，过点作交于点，

，
是正方形的对角线，
，，
，
在中，，
，
，
．
（3）①由（1）（2）可得：旋转过程中，
始终有：
·
所以当最大时，四边形的面积最大，
即当三点共线时，面积最大，
如图，

此时：
所以四边形的最大面积为：
故答案为：
②如图，连接 同理可得：

，，，分别是，，，的中点，


四边形是平行四边形，
同理可证：
四边形是正方形，
故答案为：正方形.
6．（2021·鞍山市华育高新区学校九年级月考）如图，已知正方形ABCD，直线BC上任意一点E，连接AE，将△ABE绕点A逆时针旋转α（0°＜α＜360°）得到△AFG，直线BF、EG交于点M．
（1）如图1，当点E在线段BC上，α＝90°时，求证：M为GE的中点；
（2）如图2，当点E在射线BC上，（1）中的结论是否发生变化，说明理由．
（3）当AB＝4，BE＝5，BM＝时，求DM的长（直接写出结果）．

【答案】（1）见解析；（2）不发生变化，理由见解析；（3）1
【解题思路分析】（1）将△ABE绕点A逆时针旋转α 得到△AFG， 当点E在线段BC上，α＝90°时，过作，证明四边形是平行四边形，即可得是的中点；
（2）过点作,交的延长线于点，连接,，方法同（1）证明四边形是平行四边形即可；
（3）根据勾股定理求得，①当在射线上时，根据（2）的结论，取的中点，连接，根据直角三角形斜边上的中线等于斜边的一半，三角形中位线定理，可得，进而证明是矩形，进而求得，②当在射线上时，可得此情况不符合题意，综合①②可得结果．
【解析】（1）过作,
如图，

四边形是正方形，




将△ABE绕点A逆时针旋转α得到△AFG，,



三点共线


四边形是平行四边形
为的中点；
（2）（1）中的结论，是的中点，仍然成立，
理由如下：
如图，过点作,交的延长线于点，连接,

将△ABE绕点A逆时针旋转α得到△AFG，,
,
设

四边形是正方形，

,






四边形是平行四边形
是的中点
（3）AB＝4，BE＝5，BM＝
四边形是正方形，
,
中，

将△ABE绕点A逆时针旋转α得到△AFG,
,,
①当在射线上时，如图，取的中点，连接
则


由（2）可知为的中点，



四边形是平行四边形

即
四边形是矩形
即三点共线，如图，


②当在射线上时，如图，作于点，

将△ABE绕点A逆时针旋转α得到△AFG,
,,，
，
，

平分


与不存在交点，故此情况不存在
综上所述，
7．（2021·福建省福州第八中学九年级月考）（一）问题情境：如图1，已知点E，F分别在正方形的边，上，且，点M为的中点，连接，．

（1）线段与之间的数量关系是________，位置关系是________．
（二）猜想证明：
（2）如图2，将线段和绕点B逆时针旋转，旋转角均为（）．点M为线段的中点，连接，请你判断（1）中的两个结论是否仍然成立．若成立，请证明；若不成立，请说明理由．
（三）探索发现：
（3）将图1中的线段和绕点B逆时针旋转，旋转角为，点M为线段的中点，得到如图3所示的图形，请你判断线段与之间的数量关系是否发生变化，请说明理由．
【答案】（1）；（2）两个结论成立，理由见解析；（3）线段与之间的数量关系没有发生变化，理由见解析．
【解题思路分析】（1）先证明，根据全等三角形的性质得到，由AM=MF，得到进而推出，得到，据此推出即可解题；
（2）（1）中两个结论仍然成立，延长到点N，使，连接，证明即可解题；
（3）线段与之间的数量关系没有发生变化，方法一、代数法证明；方法二、连接，连接并延长交于点G，连接，过点G作于点H，由等腰直角三角形的判定与性质证明即可．
【解析】解：（1）；
理由：如图，

∵四边形ABCD是正方形，
∴AB=BC
∵



∴
∴
∵
∴
∴
故答案为：；
（2）（1）中的两个结论仍然成立；
证明：如图，延长到点N，使，连接，

∵M为的中点，B为的中点，
∴为的中位线，
∴，
∵四边形为正方形，
∴，
∵．
∴，
即．
在和中，
，
∴，
∴，
∴，
∵为的中位线，
∴，
∴，
又∵，
∴，
∴，
∵，
∴，
∴；
（3）线段与之间的数量关系没有发生变化．
理由如下：
方法一、
设，则，
∵点M为的中点，
∴，
∴，
∴．
方法二、
连接，连接并延长交于点G，连接，过点G作于点H，

∵，
∴，
∴，
∴，
∴，
∵M为的中点，
∴，
∴四边形是矩形，
∴，
∴．
8．（2021·哈尔滨市第六十九中学校九年级月考）已知，E为正方形ABCD中CD边上一点，连接BE，过点C作CF⊥BE交AD于F，垂足为G．
（1）如图1，求证：CE＝DF；
（2）如图2，连接AG、BF，交于点H，求证：∠ABF＝∠AGF；
（3）如图3，在（2）的条件下，若AG＝AB＝11，求线段GH的长．

【答案】（1）证明见解析，（2）证明见解析，（3）6
【解题思路分析】（1）证明△BCE≌△CDF即可；
（2）取BF中点O，连接OA、OG，证明A、B、G、F四点共圆即可；
（3）作AK⊥BG于K，HN⊥AB于N，GM⊥AB于M，根据等腰三角形的性质得出，进而得出∠BAG的正切值，求出AH长即可．
【解析】（1）证明∵四边形ABCD是正方形，
∴CB＝CD，∠BCD＝90°，
∵CF⊥BE，
∴∠BGC＝90°，
∴∠CBE+∠GCB＝90°，∠GCB+∠DCF＝90°，
∴∠CBE＝∠DCF，
∴△CBE≌△DCF（AAS），
∴CE＝DF；
（2）取BF中点O，连接OA、OG，
∵∠BAF＝90°，
∴OA=OF=OB，
同理，OG=OF=OB，
∴A、B、G、F四点在以O为圆心，OA为半径的圆上，如图所示，
∴∠ABF＝∠AGF；

（3）作AK⊥BG于K，HN⊥AB于N，GM⊥AB于M，
∵四边形ABCD是正方形，
∴AB＝CB，∠ABC＝90°，
∵AK⊥BG，
∴∠AKB＝90°，
∴∠BAK+∠ABK＝90°，∠ABK+∠CBG＝90°，
∴∠BAK＝∠CBG，
∴△BAK≌△CBG（AAS），
∴AK＝BG；
∵AG＝AB＝11，
∴，
∴，
∴BC＝2EC，
由（1）得，DC＝2DF，
∴，
∴
∵MG∥CB，
∴∠MGB＝∠CBG，
∴MG＝2MB，AM＝11-MB，
,
解得，，（舍去），
，，
∴，
∴，
∵，
∴，
解得，，则，
，
GH=11-5=6．

9．（2021·四川省成都市七中育才学校九年级月考）正方形ABCD和正方形AEFG的边长分别为6和2，将正方形AEFG绕点A逆时针旋转．


（1）当旋转至图1位置时，连接BE，DG，线段BE和DG有何关系？请说明理由；
（2）在图1中，连接BD，BF，DF，请直接写出在旋转过程中△BDF的面积最大值；
（3）在旋转过程中，当点G，E，D在同一直线上时，请求出线段BE的长．
【答案】（1）数量关系：BE=DG，位置关系：BE⊥AG ，理由见解析；（2）30；（3）或
【解题思路分析】（1）设BE与DG交于点H，连接BD，易证明△BAE≌△DAG，从而可得BE=DG，∠ABE=∠ADG，从而易得∠HBD+∠BDH=90°，从而证得结论；
（2）取BD的中点O，连接AF、AO、FO，过点F作FH⊥BD于点H，则可得AO、AF的长，由AF+AO≥FO≥FH可得FH的最大值为AF+AO，从而可得△BDF面积最大值；
（3）分点E在线段DG上和在线段DG的延长线两种情况，连接AF交GE于点P，则在Rt△APD中由勾股定理可求得DP的长，从而BE=DG=DP±GP，即可得线段BE的长．
【解析】（1）数量关系：BE=DG，位置关系：BE⊥AG
理由如下：
如图，设BE与DG交于点H，连接BD
∵四边形ABCD、四边形AEFG都是正方形
∴∠BAD=∠EAG=90°，AB=AD，AE=AG
∴∠BAD+∠DAE=∠DAE+∠EAG
即∠BAE=∠DAG
在△BAE和△DAG中

∴△BAE≌△DAG(SAS)
∴BE=DG，∠ABE=∠ADG
∵∠ABE+∠EBD+∠BDA=90°
∴∠ADG+∠EBD+∠BDA=90°
即∠HBD+∠BDH=90°
∴BE⊥DG
故BE与DG的数量关系为：BE=DG，位置关系为：BE⊥AG

（2）如图，取BD的中点O，连接AF、AO、FO，过点F作FH⊥BD于点H

∵AB=AD，O为BD中点，∠BAD=90°
∴AO=BD
∵BD=
∴
∵四边形AEFG是正方形
∴
∵AF+AO≥FO≥FH
∴
即FH的最大值为
∵·
∴当FG最大时，△BDF的面积也最大
∴△BDF面积的最大值为；
（3）当点E在线段DG上时，如图，连接AF交DG于点P

∵四边形AEFG是正方形
∴AF⊥GE，GP=AP=
在Rt△APD中，由勾股定理得
∴DG=DP+GP=
∴
当点E在线段DG的延长线上时，如图，连接AF交DG于点P
同理可得：GP=AP=
在Rt△APD中，由勾股定理得
∴DG=DP－GP=
∴

综上所述，BE的长为或．
10．（2021·河南开封·九年级期末）已知四边形是正方形，是等腰直角三角形．

问题提出：
（1）如图1，当，分别在边，上，线段与的数量关系是　　，位置关系是　　．
类比探究：
（2）如图2，当绕点逆时针旋转时，试判断（1）中线段与的关系是否仍然成立，请利用图2给予证明；
拓展延伸：
（3）如图3，当绕点逆时针旋转时，延长交于点，交于点．，，求线段的长．
【答案】（1），；（2）仍然成立，见解析；（3）
【解题思路分析】（1）根据四边形是正方形得，，根据是等腰直角三角形得，即可证明；
（2）延长交于点，交于点，通过证明，得，，即可证明；
（3）在中，首先求出，，在中，求得，再证明，可得，最后根据设出未知数列出方程求解即可求出的长．
【解析】解：（1）四边形是正方形，
，，
∵是等腰直角三角形，
∴，
，
，
故答案为：，；
（2）仍然成立：，，理由如下：
如图2，延长交于点，交于点，

当绕点逆时针旋转，
，，，
在和中，
，
，
，，
，
，
，
；
（3）如图3，连接，延长与交于点，

四边形是正方形，
∴，，
，
又，
，，
，
，
在中，，
∴，
，
，
在中，，
，
在中，，
，
∵，，
∴，
在和中，
，
，
∴，
由（2）得：，
∴，
设，则，
∴，
解得：，
．
11．（2021·河南省淮滨县第一中学九年级开学考试） 如图，正方形的边长为，点是射线上的一个动点，连接并延长，交射线于点，将沿直线翻折，点落在点处．

（1）当时，如图，延长，交于点，
①的长为________；
②求证：．
（2）当点恰好落在对角线上时，如图，此时的长为________；________；
（3）当时，求的正弦值．
【答案】（1）①12；②见解析；（2），；（3）或．
【解题思路分析】（1）①根据△ABE∽△FCE，可得，即＝1，进而得到CF的长；②根据四边形ABCD为正方形，可得∠F＝∠BAF，由折叠可知：∠BAF＝∠MAF，即可得出∠F＝∠MAF，进而得到AM＝FM．
（2）根据∠CAE＝∠CFE，可得FC＝AC，再根据等腰Rt△ABC中，AC＝AB＝12，即可得到CF的长为12；由折叠可得，BE＝B'E，再根据等腰Rt△CEB'中，CE＝B'E＝BE，即可得出；
（3）分两种情况讨论：①点E在线段BC上，②点E在BC的延长线上，分别设DM＝x，根据Rt△ADM中，AM2＝AD2＋DM2，得到关于x的方程，求得x的值，最后根据进行计算即可．
【解析】解：①如图，由可得：，

∴，即，
∴的长为．
故答案为：．
②证明：∵四边形为正方形，
∴，
∴，
由折叠可知：，
∴，
∴．
（2）如图2，由折叠可得，∠BAE＝∠CAE，

由ABCD可得，∠BAE＝∠CFE，
∴∠CAE＝∠CFE，
∴FC＝AC，
又∵等腰Rt△ABC中，AC＝AB＝12，
∴CF＝12，
即CF的长为12，
由折叠可得，BE＝B'E，
∴等腰Rt△CEB'中，CE＝B'E＝BE，
∴；
故答案为：；；
①当点在线段上时，如图3，的延长线交于点，

由可得：，
∴，即，
∴，
由②可知．
设，则，
则，
在中，，
即，
解得：，
则，
∴．
②当点在的延长线上时，如图4

由可得：，
∴，即，
∴，
则，
设，则，
在中，，
即，
解得：，
则，
∴．
综上所述：当时，的正弦值为或．
12．（2021·重庆实验外国语学校九年级开学考试）如图，在菱形中，其对角线、交于点，以边为斜边构造，连接．
（1）如图一，为等腰三角形，且，，求的长；
（2）如图一，若为等腰三角形，求证：；
（3）如图二，若菱形的边长为，，的中点为，连接，求的最大值．

【答案】（1）；（2）见解析；（3）
【解题思路分析】（1）过点作于，交的延长线于，证，再证四边形是正方形，得出即可；
（2）同（1）证明即可；
（3）取的中点，连接，取的中点，连接，，过点作于，过点作交的延长线于．
【解析】解：（1）过点作于，交的延长线于．

四边形是菱形，
，，，
，
，都是等边三角形，
在中，
，
四边形是矩形，
，
，
，
，
，，
四边形是正方形，
，
，
．
．
（2）如图一（1）中，过点作于，交的延长线于．

，
四边形是矩形，
，
，
，
，
，，
四边形是正方形，
，
，
．
（3）如图二中，取的中点，连接，取的中点，连接，，过点作于，过点作交的延长线于．求出，根据三角形三边关系可求最值．

四边形是菱形，
，，，，
，
，，
，，
，
，
，
，，
，，
，
四边形是矩形，
，，
，
，
，，
，
，，
，
，
，
的最大值为．
13．（2021·重庆市育才中学九年级开学考试）在菱形中，以点为顶点作等腰，然后将等腰绕着点顺时针转动，已知．


（1）如图1，若点落在线段上，当时，连接交于点，当，．求的长；
（2）如图2，连接，，取的中点，连接．猜想与存在的数量关系，并证明你的猜想；
（3）如图3，在等腰绕着点顺时针转动时，设交于点，交于点．若，，时，请直接写出的值．
【答案】（1）；（2），证明见详解；（3）
【解题思路分析】（1）过点F作FH⊥AD于点H，由题意易得AB=AD，，则有，进而可证，根据全等三角形的性质可得，然后可得，则有，最后根据勾股定理可求解；
（2）延长AG到M，使得GM=AG，连接BM，由题意易证，则有，然后可证，进而问题可求证；
（3）过点N作NP⊥AE于点P，过点A作AQ⊥BD于点Q，由题意易得△AQM、△MPN是等腰直角三角形，∠ABD=30°，则有AQ=1，进而根据勾股定理可进行求解．
【解析】解：（1）过点F作FH⊥AD于点H，如图所示：


∵四边形是菱形，，
∴四边形是正方形，
∴AB=AD，，
∴，
∵，，
∴，
∴，
∴，
∴，
∵，
∴，
∵是等腰三角形，，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∴在Rt△AHF中，；
（2），证明如下：
延长AG到M，使得GM=AG，连接BM，如图所示：


∵取的中点，
∴，
∵，
∴，
∴，
∴，
∴，
∵，
∴，即，
∴，
∵四边形是菱形，
∴，
∴，
∴；
（3）过点N作NP⊥AE于点P，过点A作AQ⊥BD于点Q，如图所示：


∵，
∴△AQM、△MPN是等腰直角三角形，
∴，
∵四边形是菱形，
∴，BD平分∠ABC，
∵，，
∴，
∴∠ANP=∠ABD=30°，
∵，，
∴，
∴，
∵∠ANP=30°，
∴，
∴在Rt△APN中，，
∴，
∴，
∴，
∴．
14．（2021·绍兴市柯桥区杨汛桥镇中学九年级二模）定义：如图1，四边形EFGH的四个顶点分别在□ABCD四条边上（不与□ABCD的顶点重合），我们称四边形EFGH为□ABCD的内接四边形．

（1）如图1，若¨ABCD的内接四边形EFGH是平行四边形，求证：AE＝CG
（2）若平行四边形ABCD的内接四边形EFGH是矩形．
①请用无刻度的直尺与圆规，在图2中作出一个符合要求的矩形EFGH．（不必说明作图过程，但要保留作图痕迹）
②如图3，已知，AB＝10，H是AD的中点，HG＝2HE，求AD的长．
（3）已知，平行四边形ABCD的内接四边形EFGH是平行四边形，且，求证：点E，F，G，H中至少存在两个点是□ABCD边的中点．
【答案】（1）见解析；（2）①见解析；②10；（3）见解析
【解题思路分析】（1）连接EG，只需要证明△AEH≌△CGF即可得到结论；
（2）①根据矩形的判定条件和直径所对的圆周角是90°作图即可；②过点H作HN⊥HB，并延长NH交CD延长线于M，先证明△MDH≌△ANH，得到HM=HN，AN=MD，再由
，，得到,
设，，，然后证明△HMG∽△ENH，得到，由此求解即可；
（3）由，可以得到，设MN=h，HN=t，AB=a，AE=y，则MH=h-t，DG=a-y，则，由此即可求解．
【解析】解：（1）如图所示，连接EG，
∵四边形ABCD是平行四边形，
∴∠A=∠C，AB∥CD，
∴∠AEG=∠CGE，
∵四边形HEFG是平行四边形，
∴GF∥HE，HE=GF
∴∠HEG=∠FGE，
∵∠AEH+∠HEG=∠CGF+∠FGE，
∴∠AEH=∠CGF，
∴△AEH≌△CGF（AAS），
∴AE=CG

（2）①如图，连接BD与AC交于O，以O为圆心，以OB的长为半径画圆，分别于AB交于E，BC交于F，CD交于G，AD交于H，顺次连接E、F、G、H即为所求；
理由：直径所对的圆周角是直角，连接OG，OE，可以通过，∠ODG=∠OGD=∠OBE=OEB证明∠DOG=∠BOE，即G、O、E三点共线；

②如图，过点H作HN⊥HB，并延长NH交CD延长线于M，
∴∠HNA=∠HMD=90°
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD=10
∴∠MDH=∠NAH，
∵H是AD的中点，
∴AH=DH，
∴△MDH≌△ANH（AAS），
∴HM=HN，AN=MD，
∵，
∴，
∴,
设，，，
∵四边形HEFG是矩形，
∴∠GHE=90°，
∴∠MHG+∠EHN=90°，
又∵∠EHN+∠HEN=90°，
∴∠MHG=∠NEH，
∵∠HMG=∠ENH=90°，
∴△HMG∽△ENH，
∴，
∵HG＝2HE，
∴，
∴，，
∴，，
∴，
解得，
∴；

（3）同（2）②作辅助线
由（1）证明△AEH≌△CGF，同理可以证明△DHG≌△BFE，
∴，，DG=BE
∵，
∴，
设MN=h，HN=t，AB=a，AE=y，则MH=h-t，DG=a-y，
∵，
∴，
∴，
∴，
∴，
∴，
∴或，
∴H是AD的中点或E是AB的中点，
又∵AE=CG，
∴当E是中点的时候，G也是CD的中点，
同理当H是中点的时候，F是BC的中点，
∴点E，F，G，H中至少存在两个点是□ABCD边的中点．

15．（2021·西安高新一中实验中学九年级开学考试）（问题提出）

（1）如图1，四边形是正方形，是等边三角形，M为对角线（不含B点）上任意一点，将绕点B逆时针旋转得到，连接、，．若连接，则的形状是________．
（2）如图2，在中，，，求的最小值．
（问题解决）
（3）如图3，某高新技术开发区有一个平行四边形的公园，千米，，公园内有一个儿童游乐场E，分别从A、B、C向游乐场E修三条，求三条路的长度和（即）最小时，平行四边形公园的面积．
【答案】（1）等边三角形；（2）BC的最小值为；（3）平行四边形公园ABCD的面积为（平方米）．
【解题思路分析】（1）由旋转得BN=BM，∠MBN=60°，可判断出△BMN是等边三角形即可；
（2）设AB=a，则AC=10-a，进而根据勾股定理得出即可得出结论；
（3）先判断出点A'，E'，E，C在同一条线上，设BF=x，进而依次得出AB=2x，BC=6-2x，CF=6-x，再利用勾股定理得出，得出x=是A'C最小，进而求出A'F，BC，利用平行四边形面积公式计算即可．
【解析】（1）证明：的形状是等边三角形，理由如下;
由旋转知，BN=BM，∠MBN=60°
∴△BMN为等边三角形
故答案为：等边三角形；

（2）解：设AB=a，
∵AB+AC=10，
∴AC=10-AB=，
在Rt△ABC中，根据勾股定理得，


，
∵，
∴，即，
∴，
即BC的最小值为；
（3）解：如图3，

将△ABE绕点B逆时针旋转60°得到△A'BE'，
∴△ABE≌△A'BE'，
∴∠A'E'B=∠AEB，AB=A'B，A'E'=AE，BE'=BE，∠EBE'=60°，
∴△EBE'为等边三角形，
∴∠BE'E=∠BEE'=60°，EE'=BE，
∴AE+BE+CE=A'E'+EE'+CE，
要AE+BE+CE最小，即点A'，E'，E，C在同一条线上，即最小值为A'C，
过点A'作A'F⊥CB，交CB的延长线于F，
在Rt△A'FB中，∠A'BF=180°-∠ABA'-∠ABC=60°，
设BF=x，则A'B=2x，
根据勾股定理得，A'F=，
∵AB=A'B，
∴AB=2x，
∵AB+BC=6，
∴BC=6-AB=6-2x，
∴CF=BF+BC=6-x，
在Rt△A'FC中，根据勾股定理得，
，
∴当x=，即AB=2x=3时，最小，
此时，BC=6-3=3，A'F=，
∴平行四边形公园ABCD的面积为（平方千米）．