专题04 有关全等三角形的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

专题4 有关全等三角形的常见压轴题

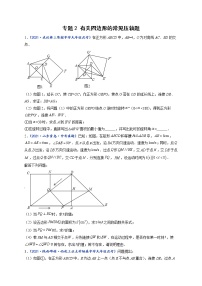
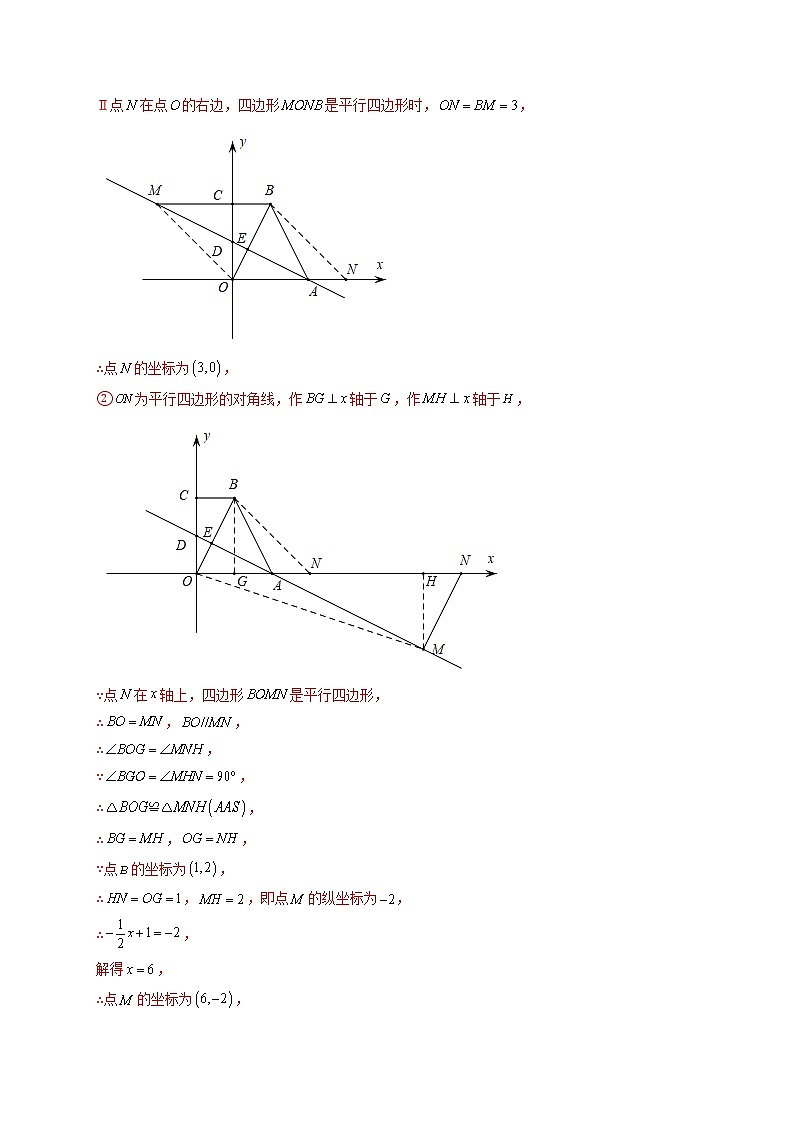
1．（2021·杏花岭·山西实验中学九年级月考）如图，平面直角坐标系中，，过作于点，为第一象限的点，过点作轴于点，连接、．

（1）求直线的解析式；

（2）若，求证：；

（3）在第（2）问条件下，若点是直线上的一个动点，在轴上存在另一个点，且以、、、为顶点的四边形是平行四边形，请直接写出点的坐标．

2．（2021·甘肃兰州十一中九年级月考）如图1，在△ABC中，AB＝AC，AD是△ABC的一条角平分线，AN为△ABC的外角∠BAM的平分线，BE⊥AN，垂足为E．已知AD＝4，BD＝3．

（1）求证：四边形ADBE是矩形；

（2）如图2，延长AD至点F，使AF＝AB，连接BF，G为BF的中点，连接EG，DG．求EG的长．

（3）如图3，在（2）问的条件下，P为BE边上的一个动点，连接PG并延长交AD延长线于点Q，连接CQ，H为CQ的中点，求点P从E点运动到B点时，点H所经过的路径长．

3．（2021·合肥市第四十八中学九年级开学考试）如图1，，分别在射线，上，且为钝角，现以线段，为斜边向的外侧作等腰直角三角形，分别是，，点，，分别是，，的中点．

（1）求证：．

（2）延长，交于点．

①如图2，若，求证：为等边三角形．

②如图3，若，求大小和的值．

4．（2021·辽宁建昌·九年级期末）已知在矩形ABCD中，∠ADC的平分线DE与BC交于点E，点P是线段DE上一定点（其中EP＜PD）

（1）如图1，若点F在CD边上（不与C，D重合），将∠DPF绕点P逆时针旋转90°后，角的两边PD，PF分别交射线DA于点H，G．

①直接写出PG与PF之间的数量关系；

②猜想DF，DG，DP的数量关系，并证明你的结论．

（2）如图2，若点F在CD的延长线上（不与D重合），将PF绕点P逆时针旋转90°，交射线DA于点G，判断（1）②中DF，DG，DP之间的数量关系是否仍然成立？若成立，给出证明；若不成立，请直接写出它们所满足的数量关系式．

5．（2021·佛山市华英学校九年级期末）已知正方形，，绕点A顺时针旋转，它的两边分别交、于点M、N，于点H．

（1）如图①，当时，可以通过证明，得到与的数量关系，这个数量关系是___________；

（2）如图②，当时，（1）中发现的与的数量关系还成立吗？说明理由；

（3）如图③，已知中，，于点H，，，求的长．

6．（2021·沭阳县怀文中学九年级月考）已知：和均为等腰直角三角形，，连接，，点为中点，连接．

（1）如图1所示，点、分别在边、上，求证：且；

（2）将绕点旋转到图2所示位置时，线段与又有怎样的关系，证明你的结论．

（3）如图3所示，当，时，求长的取值范围．

7．（2021·青海西宁·中考真题）如图，在平面直角坐标系中，一次函数的图象与x轴交于点A，与y轴交于点B，点C的坐标为，抛物线经过A，B，C三点．

（1）求抛物线的解析式；

（2）直线AD与y轴负半轴交于点D，且，求证：；

（3）在（2）的条件下，若直线与抛物线的对称轴l交于点E，连接，在第一象限内的抛物线上是否存在一点P，使四边形的面积最大？若存在，请求出点P的坐标及四边形面积的最大值；若不存在，请说明理由．

8．（2021·广州市黄埔华南师范大学附属初级中学九年级期中）在正方形中，是边上一点，且点M不与B、C重合，点在射线上，将线段绕点A顺时针旋转90°得到线段，连接，．

（1）依题意补全图1，并求证：．

（2）连接，若点，，恰好在同一条直线上，求证：．

9．（2021·哈尔滨市第十七中学校九年级二模）已知AB、AC是⊙O的两条弦，OA为半径，∠OAB＝∠OAC．

（1）如图（1），求证：AB＝AC；

（2）如图（2），延长AO交⊙O于点D，点E是BC延长线上的一点，EF切⊙O于点F，连DF交BC于点G，求证：EF＝EG；

（3）如图（3），在（2）的条件下，设DF交AC于点H，若DF∥AB，tanE＝，CH＝，求DG长．

10．（2021·河南平顶山·九年级期中）（1）阅读理解

如图1，在正方形ABCD中，若E，F分别是CD，BC边上的点，∠EAF＝45°，则我们常常会想到：把ADE绕点A顺时针旋转90°，得到ABG．易证AEF≌     ，得出线段BF，DE，EF之间的关系为    ；

（2）类比探究

如图2，在等边ABC中，D，E为BC边上的点，∠DAE＝30°，BD＝1，EC＝2．求线段DE的长；

（3）拓展应用

如图3，在ABC中，AB＝AC＝，∠BAC＝150°，点D，E在BC边上，∠DAE＝75°，若DE是等腰ADE的腰，请直接写出线段BD的长．

11．（2021·辽宁立山·九年级期中）已知：∠AOB＝∠COD＝90°，OA＝OB，OC＝OD．（OCOA）

（1）如图1：连AC、BD，判断：AC与BD之间的关系；并说明理由．

（2）若将△COD绕点O逆时针旋转，

①如图2，当点C恰好在AB边上时，请写出AC、BC、OC之间数量关系；并说明理由．

②当点B、D、C在同一条直线上时，若OB＝6，OC＝5，求AC的长．

12．（2021·广西河池·中考真题）如图，在中，，，，D，E分别是AB，BC边上的动点，以BD为直径的圆O交BC于点F．

（1）当时，求证：；

（2）当是等腰三角形且是直角三角形时，求AD的长．

13．（2021·辽宁锦州·中考真题）在△ABC中，AC＝AB，∠BAC＝，D为线段AB上的动点，连接DC，将DC绕点D顺时针旋转得到DE，连接CE，BE．

（1）如图1，当＝60°时，求证：△CAD≌△CBE；

（2）如图2，当tanα＝时，

①探究AD和BE之间的数量关系，并说明理由；

②若AC＝5，H是BC上一点，在点D移动过程中，CE＋EH是否存在最小值？若存在，请直接写出CE＋EH的最小值；若不存在，请说明理由．

14．（2021·辽宁丹东·中考真题）已知,在正方形中,点M､N为对角线上的两个动点,且,过点M、N分别作､的垂线相交于点E,垂足分别为F､G,设的面积为,的面积为,的面积为．

（1）如图（1）,当四边形为正方形时,

①求证:;

②求证:;

（2）如图（2）,当四边形为矩形时,写出,,三者之间的数量关系,并说明理由;

（3）在（2）的条件下,若,请直接写出的值．

15．（2021·山东潍坊·中考真题）如图1，在△ABC中，∠C=90°，∠ABC=30°，AC=1，D为△ABC内部的一动点（不在边上），连接BD，将线段BD绕点D逆时针旋转60°，使点B到达点F的位置；将线段AB绕点B顺时针旋转60°，使点A到达点E的位置，连接AD，CD，AE，AF，BF，EF．

（1）求证：△BDA≌△BFE；

（2）①CD+DF+FE的最小值为       ；

②当CD+DF+FE取得最小值时，求证：AD∥BF．

（3）如图2，M，N，P分别是DF，AF，AE的中点，连接MP，NP，在点D运动的过程中，请判断∠MPN的大小是否为定值．若是，求出其度数；若不是，请说明理由．