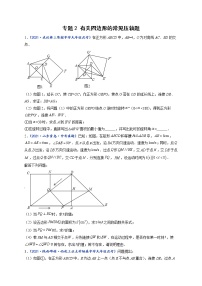
专题08 与线段有关的数量关系和位置关系的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

这是一份专题08 与线段有关的数量关系和位置关系的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1，文件包含专题08与线段有关的数量关系和位置关系的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题08与线段有关的数量关系和位置关系的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。

（1）在图1中找1条和EF相等得线段，并证明；
（2）如图2，延长DE与BC交于点H，若AG＝kGF，猜想并验证BC与CH的数量关系（用含k得式子表示）
2．（2021·辽宁省实验学校九年级月考）（1）（问题发现）：
如图1在Rt△ABC中，AB＝AC，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E与点A重合，易知△ACF∽△BCE．线段BE与AF有怎样的数量关系？请直接写出．
（2）（拓展研究）：
在（1）的条件下，将正方形CDEF绕点C旋转至如图2所示的位置，连接BE，CE，AF．请猜想线段BE和AF的数量关系，并证明你的结论；
（3）（结论运用）：
在（1）（2）的条件下，若△ABC的面积为8时，当正方形CDEF旋转到B、E、F点共线时，请直接写出线段AF的长．
3．（2021·湖北硚口·九年级月考）AC，BD是四边形ABCD的对角线，AB＝AC，∠ABC＋∠ADC＝90°．
（1）如图1．若∠ABC＝60°，求证：BD2＝AD2＋CD2；请参照大胖同学的思路完成如下证明过程．
证明：以AD为边作等边，连接BE，因为∠ABC＝60°，AB＝AC，所以是等边三角形，
（2）如图2，若∠ABC＝45°，写出一个等式，表示BD，AD，CD之间的数量关系，并给出证明；
（3）如图3，若∠ABC＝30°，ADBC，直接写出的值．
4．（2021·沈阳市光明中学九年级月考）如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
（1）①猜想如图1中线段BG、线段DE的数量关系 及所在直线的位置关系 ；
②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；
（2）将原题中正方形改为矩形（如图，且，，，，第（1）题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由；
（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为 ．
5．（2021·北京101中学九年级月考）在△ABC中，AB＝AC，∠BAC＝90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．
（1）若点D在线段BC上，如图1．请你直接写出BC与CG的数量关系是 ；位置关系是 ．
（2）若点D在线段BC的延长线上．
①请你依题意补全图2；
②判断问题（1）中的BC与CG的数量与位置关系是否仍成立，并说明理由；
③若G为CF中点，连接GE，用等式表示线段AB与GE的数量关系，并加以证明
6．（2021·广东揭阳·九年级月考）（问题情境）
如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
（探究展示）
（1）请你判断AM，AD，MC三条线段的数量关系，并说明理由；
（2）AM = DE + BM是否成立？若成立，请给出证明；若不成立，请说明理由．
（拓展延伸）
（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否仍然成立？请分别作出判断，不需要证明．
7．（2021·西城·北京四中九年级开学考试）在正方形和正方形中，，连接，H是的中点．
（1）如图1，若点B、D、F在同一直线上，求的长；
（2）在（1）条件下，连接．求线段和的数量关系和位置关系，并证明；
（3）如图2，正方形绕点D旋转，使得点H在线段的延长线上，连接，求的长度．
8．（2021·江苏锡山·九年级期中）在矩形ABCD的CD边上取一点E，将沿BE翻折至的位置．
（1）如图1，当点F落在矩形ABCD内部时，连接CF并延长，交AD于点G，若，，，则GF的长度为________________；
（2）如图2，当点C恰好落在AD边上点F处时，若，且，求BC的长；
（3）如图3，当点C恰好落在AD边上点F处时，延长EF，与的角平分线交于点M，BM交AD于点N，当时，求的值．
9．（2021·内蒙古东胜·九年级二模）（问题发现）
（1）若四边形是菱形，，点P是射线上一动点，以为边向右侧作等边，如图1，当点E在菱形内部或边上时，连接，则与有怎样的数量关系？并说明理由；
（类比探究）
（2）若四边形是正方形，点P是射线上一动点，以为直角边在边的右侧作等腰，其中，如图2.当点P在对角线上，点E恰好在边所在直线上时，则与之间的数量关系？并说明理由；
（拓展延伸）
（3）在（2）的条件下，如图3，在正方形中，，当P是对角线的延长线上一动点时，连接，若，求的面积．
10．（2021·广州市第五中学九年级开学考试）在平行四边形中，是上一点，，过点作直线，在上取一点，使得，连接．

（1）如图1，当与相交时，且．
①__________．
②猜想线段，，之间的数量关系，并证明．
（2）如图2，当与相交时，且，当时，请用线段的长表示的面积．
11．（2021·济南市章丘区第二实验中学九年级开学考试）如图，在正方形和正方形中，点，，在同一条直线上，是线段的中点，连接，．
（1）探究与的位置关系及的值（写出结论，不需要证明）；
（2）如图，将原问题中的正方形和正方形换成菱形和菱形，且度．探究与的位置关系及的值，写出你的猜想并加以证明；
（3）如图，将图中的菱形绕点顺时针旋转，使菱形的边恰好与菱形的边在同一条直线上，问题（2）中的其他条件不变．你在（2）中得到的两个结论是否发生变化？写出你的猜想并加以证明．
12．（2021·江苏淮安·中考真题）（知识再现）
学完《全等三角形》一章后，我们知道“斜边和一条直角边分别相等的两个直角三角形全等（简称HL定理）”是判定直角三角形全等的特有方法．
（简单应用）
如图（1），在△ABC中，∠BAC＝90°，AB＝AC，点D、E分别在边AC、AB上．若CE＝BD，则线段AE和线段AD的数量关系是 ．
（拓展延伸）
在△ABC中，∠BAC＝（90°＜＜180°），AB＝AC＝m，点D在边AC上．
（1）若点E在边AB上，且CE＝BD，如图（2）所示，则线段AE与线段AD相等吗？如果相等，请给出证明；如果不相等，请说明理由．
（2）若点E在BA的延长线上，且CE＝BD．试探究线段AE与线段AD的数量关系（用含有a、m的式子表示），并说明理由．
13．（2021·山东乳山·九年级模拟预测）已知：点E是矩形ABCD边AB延长线上的一动点，在矩形ABCD外作Rt，．交BC的延长线于点G，连接DF，交CG于点H．
（1）初步发现：如图1，若，．求证：．
（2）深入探究：如图2，若，．DH与HF是否仍然相等？若相等，进行证明；若不相等，写出新的数量关系并证明；
（3）拓广延伸：在（2）的条件上，，，且射线FC过边AD的三等分点，直接写出线段EF的长．
14．（2021·黑龙江牡丹江·九年级模拟预测）已知∠ABC＝60°，点F在直线BC上，以AF为边作等边三角形AFE，过点E作ED⊥AB于点D．请解答下列问题：

（1）如图①，求证：AB＋BF＝2BD；
（2）如图②、图③，线段AB，BF，BD又有怎样的数量关系？请写出你的猜想，不需要证明．
15．（2021·辽宁新抚·九年级模拟预测）如图，P为正方形ABCD对角线BD所在直线上的动点，连接CP，将CP绕点C逆时针旋转90°得线段CQ，连接DQ，DQ与直线AC相交于点M，AC与BD相交于点O．
（1）求证：PD=2OM；
（2）当P在直线BD上运动时，探究线段OP，OM，CM的数量关系，直接写出探究结论；
（3）若AB=4，DQ=6，直接写出AM的长．