专题13 动态几何类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

这是一份专题13 动态几何类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1，文件包含专题13动态几何类的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题13动态几何类的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。
（1）求直线BC的解析式；
（2）如图1，当点P在线段BC上，∠APC＝45°时，求P点坐标；
（3）如图2，当点P在直线BC上移动，将△APC沿AC翻折得到△AP′C，直线AP′与直线BC交于点D，△DCA的面积为7，求点D坐标（直接写出结果）．
【答案】（1）；（2）；（3）.
【解题思路分析】（1）用待定系数法求解析式即可．
（2）当点P在线段BC上时，得出~，进而得出，设，可得，在中，，代入求解舍去正值即可求解．
（3）过点D作DH⊥AC交AC延长线于H，利用，可得，再利用勾股定理，再利用 可得，即可求解．
【解析】解：（1）设BC直线解析式为：，
∵B（﹣4，0），C（0，3）在直线BC上，
∴代入得： ，
解得： ，
∴BC直线解析式为；
（2）当点P在线段BC上时，如下图：
∵C（0，3），A（3，0），
∴ ，△AOC为等腰直角三角形，
∴ ，
又∵ ，
∴ ，
∴~ ，
∴ ，
设 ，
∴ ，
∴ ，
过点P作PQ⊥y轴于Q，
在中， ，
，
∴（舍去正值） ，
∴，
此时 ，
∴ ，
（3）∵C（0，3），A（3，0），
∴ ,
过点D作DH⊥AC交AC延长线于H，
∵， ，
∴ ，
设 ，
∴ ，
∴ ，
∵，
∴ ，
∴ 即 ，
∴，
∴ ，
将代入得：
解得： ，
∵D在第二象限，
∴ ，
∴
∴
2．（2021·湖南广益实验中学九年级月考）已知抛物线y＝﹣x2+bx+c与x轴交于点A（m﹣2，0）和B（2m+1，0）（点A在点B的左侧），与y轴相交于点C，顶点为P，对称轴为l：x＝1．
（1）求抛物线解析式；
（2）直线y＝kx+2（k≠0）与抛物线相交于两点M（x1，y1），N（x2，y2）（x1＜x2），当|x1﹣x2|最小时，求抛物线与直线的交点M和N的坐标；
（3）首尾顺次连接点O、B、P、C构成多边形的周长为L，若线段OB在x轴上移动，求L最小值时点O、B移动后的坐标及L的最小值．
【答案】（1）y＝﹣x2+2x+3；（2）M（﹣1，0），N（1，4）；（3），，L最小值为．
【解题思路分析】（1）先根据抛物线的对称轴，确定出点A，B坐标，即可得出结论；
（2）先联立抛物线和直线MN，建立方程组，转化为关于x的一元二次方程，进而根据根与系数的关系得出x1+x2＝2﹣k，x1x2＝﹣3，再根据|x1﹣x2|最小，确定出k的值，即可得出结论；
（3）先根据平行四边形的性质得出CE＝B'P，再利用对称性得出O'C＝DC，进而判断出点D，C，E在同一条直线上时，DC+DE最小，最小值为DE，即可得出结论．
【解析】解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于点A（m﹣2，0）和B（2m+1，0），
∴，
∴m＝1，
∴点A（﹣1，0），B（3，0），
∴抛物线的解析式为y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3；
（2）由（1）知，抛物线的解析式为y＝﹣x2+2x+3，
根据题意得，，
∴x2+（k﹣2）x﹣1＝0①，
∴x1+x2＝2﹣k，x1x2＝﹣1，
∴（x1﹣x2）2＝（x1+x2）2﹣4x1x2＝（2﹣k）2+4，
要使|x1﹣x2|最小，则（x1﹣x2）2最小，
∴（k﹣2）2+4最小，
即k＝2时，|x1﹣x2|最小，
∴方程①可化为x2﹣1＝0，
∴x＝±1，
∴M（﹣1，0），N（1，4）；
（3）由（1）知，抛物线的解析式为y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴C（0，3），P（1，4），
∴，
∵B（3，0），
∴OB＝3，
如图，记OB平移后对应的点分别为O'，B'，
∴O'B'＝3，
设平移后点O'的坐标为（n，0），
则B'（n+3，0），
以CP，BP'为两边邻边作平行四边形CPB'E，
则CE＝B'P，E（n+3﹣1，0﹣1），
即E（n+2，﹣1），
过点C作直线m，使m∥x轴，作点O'关于直线m的对称点D（n，6），
∴O'C＝DC，
∵L＝CP+O'B'+O'C+B'P＝+3+DC+CE，
要使L最小，则DC+CE最小，
即点D，C，E在同一条直线上，DC+CE的最小值为DE，
∵C（0，3），
∴设直线DE的解析式为y＝k'x+3，
∴ ，
∴，
∴，，，，
∴，
∴L最小值为．
3．（2021·广东揭阳·九年级月考）如图，在Rt△ABC中，∠C＝90°，AC＝20，∠A＝60°．点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动，同时点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点P、Q运动的时间是t秒．过点P作PM⊥BC于点M，连接PQ、QM．
（1）请用含有t的式子填空：AQ＝ ，AP＝ ，PM＝
（2）是否存在某一时刻使四边形AQMP为菱形？如果存在，求出相应的t值；如果不存在，说明理由；
（3）当t为何值时，△PQM为直角三角形？请说明理由．
【答案】（1）t，40-2t，t；（2）时，四边形AQMP是菱形；（3）或时△PQM是直角三角形
【解题思路分析】（1）根据题意求出求出BP=2t，AQ=t，然后利用含30度角的直角三角形的性质求出AB=2AC=40，由此求出AP=AB-BP=40-2t，；
（2）先证明四边形AQMP是平行四边形，然后根据菱形的判定：当AP=AQ时，四边形AQMP是菱形，，解方程即可；
（3）分三种情况进行讨论：当∠MPQ=90°，当∠MQP=90°时，当∠PMQ=90°时，利用含30度角的直角三角形的性质求解即可．
【解析】解：（1）由题意可得：BP=2t，AQ=t
∵∠C＝90°，∠A＝60°
∴∠B=30°，
∴，
∴，
∵PM⊥AC，
∴∠PMB=90°，
∴，
故答案为：t，40-2t，t；
（2）存在，理由如下：
由（1）知，
∵PM⊥BC，AC⊥BC
∴PM∥AQ，
∴四边形AQMP是平行四边形，
∴当AP=AQ时，四边形AQMP是菱形，
∴，
解得，
∴当时，四边形AQMP是菱形；
（3）当△PQM为直角三角形时有三种情况：
①当∠MPQ=90°，此时四边形CMPQ是矩形，
∴∠PQA=∠PQC=90°，
∴∠APQ=30°，
∴AP=2AQ，
∴，
解得；
②当∠MQP=90°时，由（2）知MQ∥AP，
∴∠APQ=∠PQM=90°，
∴∠PQA=30°，
∴AQ=2AP，
∴，
解得；
③当∠PMQ=90°时此种情况不存在，
∴综上所述，或时△PQM是直角三角形．
4．（2021·湖北宜都·九年级期中）已知：梯形中，，对角线，平分交边于点，点是对角线上的动点，连接交于点．
（1）如（图1），若，，则的长为______．
（2）如（图2），于点，连接，，．
①求证：；
②如（图3），当时，求的值．
（3）如（图4），以点为直角顶点，在的左下方作等腰直角，，若点从点出发，沿运动到点停止，试探究：随着点的运动，的中点运动的路径是什么图形？并直接写出其路径的长与对角线长的比值．
【答案】（1）2；（2）①见解析；②；（3）点的运动路径为线段，点的路径长与对角线长的比值为
【解题思路分析】（1）由题意可判断出，从而在中，直接求解即可；
（2）①由题意直接证得，然后结合（1）中结论证明，即可得到，然后根据题目条件进行代换得到，从而得出结论即可；②过作于点，证明，得到，即可得出结论；
（3）设的中点为，连接，，结合题意与等腰直角三角形的性质证明出，然后推出，，从而得出结论即可．
【解析】（1）平分，
，
，
，
，
，
在中，，
；
（2）①中，
，
，
由（1）知，
，
，
，
，
，
，
，
即；
②过作于点，
，
，
，
，
在和中，
，
，
；
（3）当与重合时，点落在边上的点处，
设的中点为，连接，，则与均为等腰直角三角形，
，
，
又∵，
，
，，
，
∵为的中位线，
∴，，
∴如图所示，点的运动路径为线段，
∴点的路径长与对角线长的比值为，
∵，
∴，
又∵，
∴，
∴点的路径长与对角线长的比值为．
5．（2021·日照港中学九年级期中）如图，抛物线与x轴相交于A，B两点，与y轴相交于点C，OA=2，OB=4，直线l是抛物线的对称轴，在直线l右侧的抛物线上有一动点D，连接AD，BD，BC，CD．
（1）求抛物线的函数表达式．
（2）若点D在x轴的下方，当△BCD的面积是时，求△ABD的面积．
（3）在（2）的条件下，点M是x轴上一点，点N是抛物线上一动点，是否存在点N，使得以点B，D，M，N为顶点，以BD为一边的四边形是平行四边形，若存在，求出点N的坐标；若不存在，请说明理由．
【答案】（1）y＝x2−x−6（2）（3）（1−，）或（1＋，）或（−1，−）
【解题思路分析】（1）根据OA＝2，OB＝4确定点A和B的坐标，代入抛物线的解析式列方程组解出即可；
（2）如图1，过D作DG⊥x轴于G，交BC于H，利用待定系数法求直线BC的解析式，设D（x，x2−x−6），则H（x，x−6），表示DH的长，根据△BCD的面积是，列方程可得x的值，因为D在对称轴的右侧，所以x＝1不符合题意，舍去，利用三角形面积公式可得结论；
（3）分两种情况：N在x轴的上方和下方，根据y＝±确定N的坐标，并正确画图．
【解析】解：（1）∵OA＝2，OB＝4，
∴A（−2，0），B（4，0），
把A（−2，0），B（4，0）代入抛物线y＝ax2＋bx−6中得：
，
解得：，
∴抛物线的解析式为：y＝x2−x−6；
（2）如图1，过D作DG⊥x轴于G，交BC于H，
当x＝0时，y＝−6，
∴C（0，−6），
设BC的解析式为：y＝kx＋n，
则，解得：，
∴BC的解析式为：y＝x−6，
设D（x，x2−x−6），则H（x，x−6），
∴DH＝x−6−（x2−x−6）＝−x2＋3x，
∵△BCD的面积是，
∴DH•OB＝，
∴×4×(−x2＋3x)＝，
解得：x＝1或3，
∵点D在直线l右侧的抛物线上，
∴D（3，−），
∴△ABD的面积＝AB•DG＝×6×＝；
（3）分两种情况：
①如图2，N在x轴的上方时，四边形MNBD是平行四边形，
∵B（4，0），D（3，−），且M在x轴上，
∴N的纵坐标为，
当y＝时，即x2−x−6＝，
解得：x＝1＋或1−，
∴N（1−，）或（1＋，）；
②如图3，点N在x轴的下方时，四边形BDNM是平行四边形，此时M与O重合，
∴N（−1，−）；
综上，点N的坐标为：（1−，）或（1＋，）或（−1，−）．
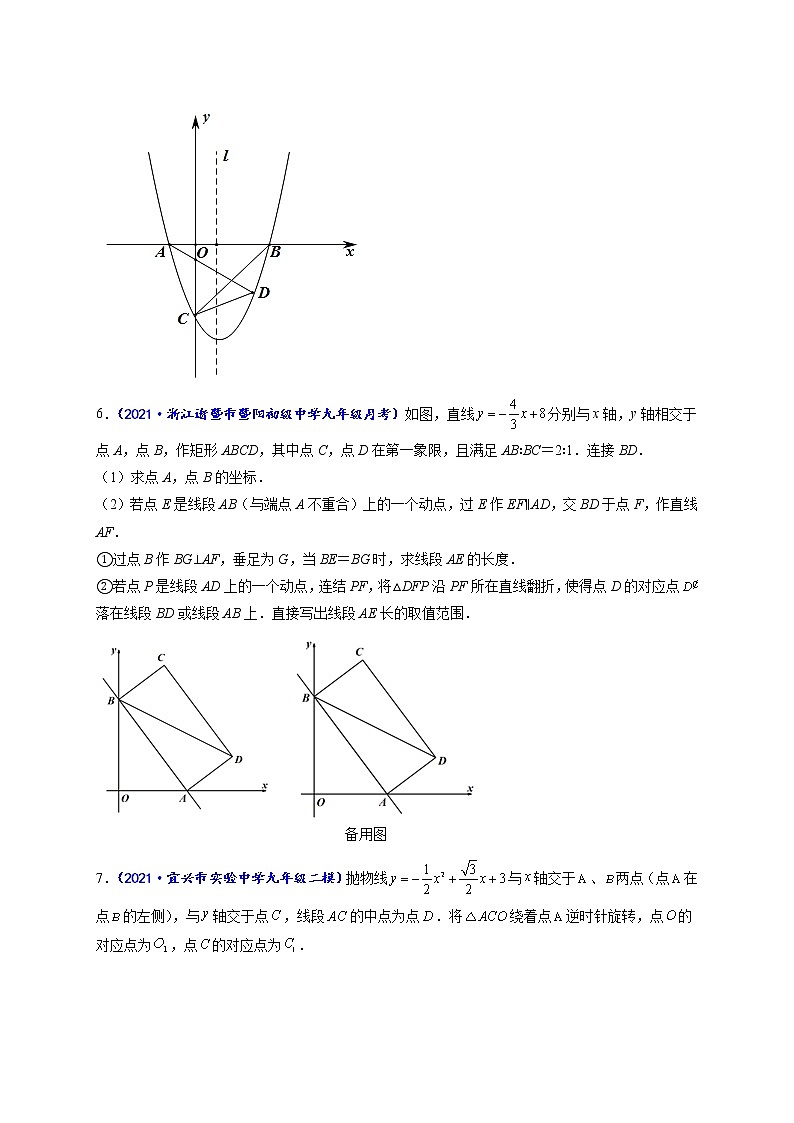
6．（2021·浙江诸暨市暨阳初级中学九年级月考）如图，直线分别与x轴，y轴相交于点A，点B，作矩形ABCD，其中点C，点D在第一象限，且满足AB∶BC＝2∶1．连接BD．
（1）求点A，点B的坐标．
（2）若点E是线段AB（与端点A不重合）上的一个动点，过E作EF∥AD，交BD于点F，作直线AF．
①过点B作BG⊥AF，垂足为G，当BE＝BG时，求线段AE的长度．
②若点P是线段AD上的一个动点，连结PF，将△DFP沿PF所在直线翻折，使得点D的对应点落在线段BD或线段AB上．直接写出线段AE长的取值范围．
【答案】（1）A（6，0），B（0，8）；（2）①4；②或
【解题思路分析】（1）分别令中x=0、y=0，求出与之对应的y、x值，由此即可得出点A，点B的坐标；
（2）由题意证，得出AF＝AD，设BE＝x，EF＝0.5x，AE＝10－x，即可求出线段AE的长度； 在线段AB上时：（考虑以F为圆心的圆与AB相交的情况），分情况讨论即可．
【解析】（1）令中x=0，则y=8，
；
令中y=0，则x=6，
；
（2）①由BE＝BG，
，
，
∠BDA＝∠BFE＝∠BFG＝∠AFD，可得：AF＝AD，
，
，
又 AB∶BC＝2∶1，
，
，
设BE＝x，EF＝0.5x，AE＝10－x，
在Rt△AEF中：，
可得x＝6，AE＝4；
②当在BD上时，
当P与A重合时，AE最长，
即时，AE最长，
~~，
，
，
，
，
，
当时，可把翻折到BD上；
当在线段AB上时：
当DP＝P时，与A重合，
PF为AD中垂线，PF为中位线，
AE＝5，
（若此时E再上移，以F为圆心，FD为半径作圆，与AB不会有交点，所以）；
当FE＝FD时：与 E重合，
设则，
，
由，得：，
，
，即，
当在AB上时，．
综上，或．
7．（2021·宜兴市实验中学九年级二模）抛物线与轴交于、两点（点在点的左侧），与轴交于点，线段的中点为点．将绕着点逆时针旋转，点的对应点为，点的对应点为．
（1）求、、三点的坐标；
（2）当旋转至时，求此时、两点间的距离；
（3）点是线段上的动点，旋转后的对应点为，当恰巧落在边上时，连接，，试求最小时点的坐标；
（4）连接，，则在旋转过程中，的面积是否存在最大值？若存在，直接写出最大值，若不存在，说明理由．
【答案】（1）A（-，0）、B（2，0）、C（0，3）；（2）6；（3）P（0，1）；（4）3．
【解题思路分析】（1）令y=0建立一元二次方程，求其根即得到A，B的横坐标，令x=0，得到y值即得到点C的坐标；
（2）分两种情形计算即可，注意三角形全等和三点共线原理的运用；
（3）利用旋转的全等性，把线段和的最小值问题转化为将军饮马河问题，利用函数的解析式确定坐标即可；
（4）根据旋转的全等性质，得到OC==3，直角三角形的性质AD=DO=AO=，得到点O在以A为圆心，半径为的圆上，故当DO是圆的直径时，三角形面积最大．
【解析】（1）∵，
令y=0得，
解得，
∵点在点的左侧，
∴A（-，0）、B（2，0）；
令x=0，得到y=3，
∴点C的坐标（0，3）；
（2）当点落在x轴的负半轴上时，
∵A（-，0）,C（0，3）,
∴OA=，OC=3，
∴tan∠ACO=，
∴∠ACO=30°，∠OAC=60°，
根据旋转的性质，得∠A=30°，∠ A =60°，
∵ A=OA，
∴∠AO=∠A O = 30°，
∴∠O C=60°，
∵ O=3=OC，
∴△O C是等边三角形，
∴ C= O C，
∵AO=AO，
∴△A C≌△AOC，
∴∠AC= ∠AOC= 90°，
∴∠A+ ∠AC =180°，
∴、、C三点一线，
∴C=6；
当点落在y轴的负半轴上时，C=2OC=6；
（3）根据旋转的性质,得=AP，∴=AP+
作点关于Y轴的对称点M，
作直线AM，交y轴与点P，此时的点P就是取得最小值的位置，
∵A（-，0）,C（0，3）,
∴OA=，OC=3，
∴tan∠ACO=，
∴∠ACO=30°，∠OAC=60°，
∴A=，
过点作N⊥x轴，垂足为N，
∴AN=，N=，
∴（-，），∴M（，），
设直线AM的解析式为y=kx+b，根据题意，得
，解得，
∴直线AM的解析式为y=x+1，令x=0，得y=1，
∴P（0，1）；
（4）根据旋转的全等性质，得到OC==3，在直角三角形AOC中，根据直角三角形的性质AD=DO=AO=，得到点O在以A为圆心，半径为的圆上，
故当D是圆的直径时，三角形面积最大，面积最大值为：=3．
8．（2021·江苏盱眙·九年级期中）如图，二次函数的图象与坐标轴交于A、B、C三点，该二次函数图象的顶点为D，连接AC，BC．
（1）直接写出D点的坐标： ；
（2）如图①，求△ABC的面积；
（3）点P在线段CO上运动．
①如图②，直线BP交AC干点M，交该二次函数图象于点N，若，求N点坐标；
②如图③，在线段AO上有一点，连接PD，请探究在P点的运动过程中，的值是否能为？如能，直接写出此时P点坐标；若不能，说明理由．
【答案】（1）（1，）；（2）8；（3）① N（）；②存在点P，点P的坐标为（0，）或（0，）．
【解题思路分析】（1）将解析式配方为顶点式，即可得到顶点坐标；
（2）先分别求出点A、B、C的坐标，再根据三角形的面积公式计算得到答案；
（3）①先求出直线AC的解析式，设点M的坐标为（），根据，求出m，得到直线BM的解析式，解，即可得到点N的坐标；
②先求出，AC=5，若存在点P，在P点的运动过程中，的值是否能为，则∠APD=∠ACO，推出∠CAP=∠OPD，过点D作DE⊥AC于点E，设点P的坐标为（0，n），根据tan∠CAP= tan∠OPD，得到，列得，计算求出n的值，根据判断得出点P的存在性．
【解析】解：（1）∵，
∴D点的坐标为（1，），
故答案为：（1，）；
（2）令中y=0，得，解得，
令x=0，得y=4，
∴A（-3,0），B（1,0），C（0,4），
∴AB=4，
∴；
（3）①∵A（-3,0），C（0,4），
∴直线AC的解析式为，
设点M的坐标为（），
∵，
∴-m：1=2:1，
解得m=-2，
∴M（-2，），
∴直线BM的解析式为
解，得，
，
∴N（）；
②∵OA=3，OC=4，
∴，AC=5，
若存在点P，在P点的运动过程中，的值能为，则∠APD=∠ACO，
∵∠APO=∠APD+∠OPD=∠ACO+∠CAP，
∴∠CAP=∠OPD，
过点D作DE⊥AC于点E，
设点P的坐标为（0，n），
∴CP=4-n，
∴,
∴，
∵，
∴OD=，
∵tan∠CAP= tan∠OPD，
∴，
∴，
解得，
∵，
∴存在点P，点P的坐标为（0，）或（0，）．
9．（2021·山东莱西·九年级期中）如图所示，四边形ABCD为矩形，AB＝6cm，AD＝4cm，若点Q从A点出发沿AD以1cm/s的速度向D运动，P从B点出发沿BA以2cm/s的速度向A运动，如果P、Q分别同时出发，当一个点到达终点时，另一点也同时停止．设运动的时间为t（s）．
（1）当t为何值时，△PAQ为等腰三角形？
（2）当t为何值时，△APD的面积为6cm2？
（3）五边形PBCDQ的面积能否达到20cm2？若能，请求出t的值；若不能，请说明理由．
（4）当t为何值时，P、Q两点之间的距离为cm？
【答案】（1）当t＝2时，△PAQ为等腰三角形；（2）当t＝时，△APD的面积为6cm2；（3）五边形PBCDQ的面积不能达到20cm2；（4）t＝
【解题思路分析】（1）根据点在矩形边上的运动速度和时间，分别确定AQ＝tcm，BP＝2tcm，得出cm，再根据为等腰三角形，，将相等的边代入计算即可求出t值；
（2）由（1）得：cm，cm，根据三角形面积公式及题目要求可得：，求解一元一次方程即可得出答案；
（3）根据图形可得：矩形ABCD的面积减去△PAQ的面积即为五边形的面积，代入可得关于t的一个代数式，根据题意可得：，然后利用一元二次方程根的判别式即可确定方程是否有解，即面积能否达到20cm2；
（4）利用勾股定理及根据题意可得：，然后求解，最后要考虑题意中点的运动时间是否都符合题意，不符合题意的舍去，即可得出t值．
【解析】解：（1）根据题意，AQ＝tcm，BP＝2tcm，AP＝（6﹣2t）cm，
∵为等腰三角形，，
∴，即，
解得：，
∴当时，△PAQ为等腰三角形；
（2）∵（cm2），
∴，
解得：，
∴当时，的面积为6cm2；
（3）∵（cm2），
∴
整理得：，
∵，
∴该方程没有实数根，
∴五边形PBCDQ的面积不能达到20cm2；
（4）在Rt△APQ中，，
根据题意得：，
∴化简后得：，
解得：，，
∵，，
∴，
∴（舍去），
∴．
10．（2020·山东南区·九年级期末）在菱形ABCD中，对角线AC、BD交于点O，且AC＝16cm，BD＝12cm．点P从点A出发，沿AD方向匀速运动，速度为2cm/s；点Q从点C出发，沿CO方向匀速运动，速度为1cm/s．若P、Q两点同时出发，过点Q作，交BD于点M，设运动时间为t（s）（0＜t≤4）．解答下列问题：
（1）当t为何值时，？
（2）设四边形AMQP的面积为S1，四边形PQCD的面积为S2，S＝S1﹣S2，求S关于t的函数关系式；并求出当t为何值时，S的值最大，最大值是多少？
（3）求是否存在某一时刻t，使点P在MQ的垂直平分线上？如果存在，求出此时t的值；如果不存在，请说明理由．
【答案】（1）t＝；（2）S＝﹣+t（0＜t≤4），当t＝4时，S值最大，此时S＝；（3）存在，t＝
【解题思路分析】（1）如图1，延长PQ交BC于点E，过点E作EF⊥AC，证明Rt△CEF∽Rt△CBO，即可得出答案；
（2）如图2，过点P作PG⊥AC于点G，通过S＝S△AMQ+2S△APQ﹣S△ACD，得出S＝﹣+t（0＜t≤4），运用二次函数性质即可求得答案；
（3）先证明△KMN∽△CBO，求出DK＝t+，再通过△KDP∽△CBO，求出DP，从而建立方程求解即可．
【解析】解：（1）如图1，延长PQ交BC于点E，过点E作EF⊥AC，
∵AC＝16cm，BD＝12cm，菱形ABCD，
∴AC⊥BD，OB＝OD＝BD，OA＝OC＝AC，
∴AD＝10cm，CO＝8cm，
∴PD＝10﹣2t，
∵PQDC，PDEC，
∴四边形PDCE是平行四边形，
∴PD＝EC＝10﹣2t，FC＝QC＝t，
∵EF⊥AC，AC⊥BD，
∴EFBD，
∴Rt△CEF∽Rt△CBO，
∴，即，
∴t＝.
（2）如图2，过点P作PG⊥AC于点G，
∵S1＝S△AMQ+S△APQ，
S2＝S△ACD﹣S△APQ，
∴S＝S△AMQ+2S△APQ﹣S△ACD，
∵OC＝8，CQ＝t，
∴OQ＝8﹣t，AQ＝16﹣t，
∵MQBC，
∴，即，
∴MO＝6﹣t，
∵PG⊥AC，AC⊥BD，AP＝2t，
∴PGBD，
∴Rt△APG∽Rt△ADO，
∴，
∴PG＝t，
∴S＝S△AMQ+2S△APQ﹣S△ACD
＝AQ•OM+2×AQ•PG﹣AC•OD
＝（16﹣t）（6﹣t）+2×（16﹣t）（t）﹣×16×6
＝﹣+t（0＜t≤4），
∵﹣＝＞4，且0＜t≤4，
∴S随t的增大而增大，
∴当t＝4时，S值最大，此时S＝．
（3）存在，t＝时，点P在MQ的垂直平分线上．
如图3，由（2）得：CQ＝t，OQ＝8﹣t，AP＝2t，
∴DP＝10﹣2t，MQ＝（8﹣t），
∵PN垂直平分MQ，
∴MN＝MQ＝（8﹣t），∠MNK＝90°，
∵MQBC，
∴∠KMN＝∠OBC，BM＝t，
∴△KMN∽△CBO，
∴，即，
∴MK＝（8﹣t），
∴DK＝BD﹣BM﹣MK＝12﹣t﹣（8﹣t）＝t+，
∵MQAD，
∴△KDP∽△KMN，
∴△KDP∽△CBO，
∴＝，
∴DP＝×DK＝，
∴＝10﹣2t，
解得：t＝．
11．如图所示，在平面直角坐标系中，点B的坐标为（4，8），过点B分别作BA⊥y轴，BC⊥x轴，得到一个长方形OABC，D为y轴上的一点，将长方形OABC沿着直线DM折叠，使得点A与点C重合，点B落在点F处，直线DM交BC于点E．
（1）直接写出点D的坐标 ；
（2）若点P为x轴上一点，是否存在点P使△PDE的周长最小？若存在，请求出△PDE的最小周长；若不存在，请说明理由．
（3）在（2）的条件下，若Q点是线段DE上一点（不含端点），连接PQ．有一动点H从P点出发，沿线段PQ以每秒1个单位的速度运动到点Q，再沿着线段QE以每秒个单位长度的速度运动到点E后停止．请直接写出点H在整个运动过程中所用的最少时间t，以及此时点Q的坐标．
【答案】（1）D（0，3）；（2）存在，6；（3）5秒，Q（，）
【解题思路分析】（1）设D（0，m），且m＞0，运用矩形性质和折叠性质可得：OD＝m，OA＝8，CD＝8﹣m，再利用勾股定理建立方程求解即可；
（2）如图1，作点D关于x轴的对称点D′，连接D′E，交x轴于点P，则点P即为所求，此时△PDE的周长最小，运用勾股定理可得CE＝5，BE＝3，作EG⊥OA，在Rt△DEG中，可得DE＝，在Rt△D′EG中，可得，即可求出答案；
（3）运用待定系数法求得直线D′E的解析式为y＝2x﹣3，进而求得P（，0），过点E作EG⊥y轴于点G，过点Q、P分别作y轴的平行线，分别交EG于点H、H′，H′P交DE于点Q′，利用待定系数法可得直线DE的解析式为y＝x+3，设Q（t，t+3），则H（t，5），再运用勾股定理即可求出答案．
【解析】解：（1）设D（0，m），且m＞0，
∴OD＝m，
∵四边形OABC是矩形，
∴OA＝BC＝8，AB＝OC＝4，∠AOC＝90°，
∵将长方形OABC沿着直线DM折叠，使得点A与点C重合，
∴CD＝AD＝OA﹣OD＝8﹣m，
在Rt△CDO中，OD2+OC2＝CD2，
∴m2+42＝（8﹣m）2，
解得：m＝3，
∴点D的坐标为（0，3）；
（2）存在．
如图1，作点D关于x轴的对称点D′，连接D′E，交x轴于点P，则点P即为所求，
此时△PDE的周长最小，
在Rt△CEF中，BE＝EF＝BC﹣CE，EF2+CF2＝CE2，BC＝8，CF＝4，
∴CE＝5，BE＝3，
作EG⊥OA，
∵OD＝AG＝BE＝3，OA＝8，
∴DG＝2，
在Rt△DEG中，EG2+DG2＝DE2，EG＝4，
∴DE＝，
在Rt△D′EG中，EG2+D′G2＝D′E2，EG＝4，D′G＝8，
∴D′E＝，
∴△PDE周长的最小值为DE+D′E＝；
（3）由（2）得，E（4，5），D′（0，﹣3），
设直线D′E的解析式为y＝kx+b，
则，
解得：，
∴直线D′E的解析式为y＝2x﹣3，
令y＝0，得2x﹣3＝0，
解得：x＝，
∴P（，0），
过点E作EG⊥y轴于点G，过点Q、P分别作y轴的平行线，分别交EG于点H、H′，H′P交DE于点Q′，
设直线DE的解析式为y＝k′x+b′，
则，
解得：，
∴直线DE的解析式为y＝x+3，
设Q（t，t+3），则H（t，5），
∴QH＝5﹣（t+3）＝2﹣t，EH＝4﹣t，
由勾股定理得：DE＝＝（2﹣t）＝QH，
∴点H在整个运动过程中所用时间＝＝PQ+QH，
当P、Q、H在一条直线上时，PQ+QH最小，即为PH′＝5，点Q坐标（，），
故：点H在整个运动过程中所用最少时间为5秒，此时点Q的坐标（，）．
12．（2021·四川成都·中考真题）在中，，将绕点B顺时针旋转得到，其中点A，C的对应点分别为点，．
（1）如图1，当点落在的延长线上时，求的长；
（2）如图2，当点落在的延长线上时，连接，交于点M，求的长；
（3）如图3，连接，直线交于点D，点E为的中点，连接．在旋转过程中，是否存在最小值？若存在，求出的最小值；若不存在，请说明理由．
【答案】（1）；（2）；（3）存在，最小值为1
【解题思路分析】（1）根据题意利用勾股定理可求出AC长为4．再根据旋转的性质可知，最后由等腰三角形的性质即可求出的长．
（2）作交于点D，作交于点E．由旋转可得，．再由平行线的性质可知，即可推出，从而间接求出，．由三角形面积公式可求出．再利用勾股定理即可求出，进而求出．最后利用平行线分线段成比例即可求出的长．
（3）作且交延长线于点P，连接．由题意易证明，
，，即得出．再由平行线性质可知，即得出，即可证明，由此即易证，得出，即点D为中点．从而证明DE为的中位线，即．即要使DE最小，最小即可．根据三角形三边关系可得当点三点共线时最小，且最小值即为，由此即可求出DE的最小值．
【解析】（1）在中，．
根据旋转性质可知，即为等腰三角形．
∵，即，
∴，
∴．
（2）如图，作交于点D，作交于点E．
由旋转可得，．
∵，
∴，
∴，
∴，．
∵，即，
∴．
在中，，
∴．
∴．
∵，
∴，即，
∴．
（3）如图，作且交延长线于点P，连接．
∵，
∴，
∵，即，
又∵，
∴．
∵，
∴，
∴，
∴，
∴．
∴在和中 ，
∴，
∴，即点D为中点．
∵点E为AC中点，
∴DE为的中位线，
∴，
即要使DE最小，最小即可．
根据图可知，即当点三点共线时最小，且最小值为．
∴此时，即DE最小值为1．
13．（2021·海南中考真题）已知抛物线与x轴交于两点，与y轴交于C点，且点A的坐标为、点C的坐标为．
（1）求该抛物线的函数表达式；
（2）如图1，若该抛物线的顶点为P，求的面积；
（3）如图2，有两动点在的边上运动，速度均为每秒1个单位长度，它们分别从点C和点B同时出发，点D沿折线按方向向终点B运动，点E沿线段按方向向终点C运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，请解答下列问题：
①当t为何值时，的面积等于；
②在点运动过程中，该抛物线上存在点F，使得依次连接得到的四边形是平行四边形，请直接写出所有符合条件的点F的坐标．
【答案】（1）；（2）的面积为；（3）①当或时，；②点F的坐标为或．
【解题思路分析】（1）直接将两点坐标代入解析式中求出a和c的值即可；
（2）先求出顶点和B点坐标，再利用割补法，将所求三角形面积转化为与其相关的图形的面积的和差关系即可，如图，；
（3）①先求出BC的长和E点坐标，再分两种情况讨论，当点D在线段上运动时的情况和当点D在线段上运动情况，利用面积已知得到关于t的一元二次方程，解t即可；
②分别讨论当点D在线段上运动时的情况和当点D在线段上的情况，利用平行四边形的性质和平移的知识表示出F点的坐标，再代入抛物线解析式中计算即可．
【解析】（1）∵抛物线经过两点，

解得
该地物线的函数表达式为
（2）∵抛物线，
∴抛物线的顶点P的坐标为．
，令，解得：，
点的坐标为．
如图4-1，连接，则

的面积为．
（3）①∵在中，．
当动点E运动到终点C时，另一个动点D也停止运动．
，
∴在中，．
当运动时间为t秒时，，
如图4-2，过点E作轴，垂足为N，则~．
．
．
∴点E的坐标为．
下面分两种情形讨论：
i．当点D在线段上运动时，．
此时，点D的坐标为．

当时，．
解得（舍去），．
．
ii．如图4-3，当点D在线段上运动时，，
．
当时，
解得．
又，
．
综上所述，当或时，
②如图4-4，当点D在线段上运动时，；
∵，
当四边形ADFE为平行四边形时，
AE可通过平移得到EF，
∵A到D横坐标加1，纵坐标加，
∴，
∴，
化简得：，
∴，
∴，
∴;
如图4-5，当点D在线段上运动时，
AE可通过平移得到EF，
∵，
∵A到D横坐标加，纵坐标不变，
∴，
∴
∴，
因为，
∴，
∴，
综上可得，F点的坐标为或．

14．（2021·江苏南京·中考真题）在几何体表面上，蚂蚁怎样爬行路径最短？
（1）如图①，圆锥的母线长为，B为母线的中点，点A在底面圆周上，的长为．在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径，并标出它的长（结果保留根号）．
（2）图③中的几何体由底面半径相同的圆锥和圆柱组成．O是圆锥的顶点，点A在圆柱的底面圆周上．设圆锥的母线长为l，圆柱的高为h．
①蚂蚁从点A爬行到点O的最短路径的长为________（用含l，h的代数式表示）．
②设的长为a，点B在母线上，．圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路．
【答案】（1）作图如图所示；（2）①h +l；②见解析．
【解题思路分析】（1）根据两点之间线段最短，即可得到最短路径；连接OA，AC，可以利用弧长与母线长求出∠AOC，进而证明出△OAC是等边三角形，利用三角函数即可求解；
（2）①由于圆锥底面圆周上的任意一点到圆锥顶点的距离都等于母线长，因此只要蚂蚁从点A爬到圆锥底面圆周上的路径最短即可，因此顺着圆柱侧面的高爬行，所以得出最短路径长即为圆柱的高h加上圆锥的母线长l；
②如图，根据已知条件，设出线段GC的长后，即可用它分别表示出OE、BE、GE、AF，进一步可以表示出BG、GA，根据B、G、A三点共线，在Rt△ABH中利用勾股定理建立方程即可求出GC的长，最后依次代入前面线段表达式中即可求出最短路径长．
【解析】解：（1）如图所示，线段AB即为蚂蚁从点A爬行到点B的最短路径；
设∠AOC=n°，
∵圆锥的母线长为， 的长为，
∴，
∴；
连接OA、CA，
∵，
∴是等边三角形，
∵B为母线的中点，
∴，
∴．
（2）① 蚂蚁从点A爬行到点O的最短路径为：先沿着过A点且垂直于地面的直线爬到圆柱的上底面圆周上，再沿圆锥母线爬到顶点O上，因此，最短路径长为h+l
② 蚂蚁从点A爬行到点B的最短路径的示意图如下图所示，线段AB即为其最短路径（G点为蚂蚁在圆柱上底面圆周上经过的点，图中两个C点为图形展开前图中的C点）；
求最短路径的长的思路如下：如图，连接OG，并过G点作GF⊥AD，垂足为F，由题可知，，GF=h， OB=b，
由的长为a，得展开后的线段AD=a，设线段GC的长为x，则的弧长也为x，由母线长为l，可求出∠COG，
作BE⊥OG，垂足为E，
因为OB=b，可由三角函数求出OE和BE，从而得到GE，利用勾股定理表示出BG，
接着由FD=CG=x，得到AF=a-x，利用勾股定理可以求出AG，
将AF+BE即得到AH，将EG+GF即得到HB，
因为两点之间线段最短，∴A、G、B三点共线，
利用勾股定理可以得到：,进而得到关于x的方程，即可解出x，
将x的值回代到BG和AG中，求出它们的和即可得到最短路径的长．
15．（2021·江苏邗江·九年级二模）如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为cm/s（当P、Q两个点中有一个点到达终点时，即停止）．连接PQ，设P的运动的时间为t（单位：s）．设CQ=y，运动时间为x（s），y与x函数关系如图②所示：
解答下列问题：
（1）的值_______________；当_______________时，；
（2）设面积为S（单位：cm2），当t为何值时，S取得最大值，并求出最大值．
（3）是否存在某一时刻使得为等腰三角形，如果存在请直接写出t的值，如果不存在请说明理由．
（4）如图3连接BQ、CP交于点E，求当时，t的值．
【答案】（1）2；；（2）当时，S取得最大值，最大值为；（3）存在，；（4）
【解题思路分析】（1）利用图2中的坐标（2,4）代入图1的相关线段中进行运算即可求出速度a，再利用得到关于t的方程，即可求出t；
（2）通过作辅助线构造直角三角形，利用相似得到，再利用三角形面积公式得到关于t的二次函数，利用二次函数的性质即可求出面积最大值；
（3）分三种情况讨论，当时和当时，可利用勾股定理建立方程，求出t的值，当时，直接建立一元一次方程求解即可；
（4）利用角的关系，先得到，再得到，最后得到，利用相似的性质即可求解．
【解析】解：（1）由图2可知，当运动2s时，CQ=4，
∴AQ=8-4=4，
所以运动时间为4÷2=2（m/s）；
要使，则有,即，
解得：；
故答案为：2；；
（2）如答图1所示，过P点作于点D．
∴，
∴，
即，
解得．
，
∴当时，S取得最大值，最大值为．
（3）存在，如解答图1所示，由（2）知，
同理，，得：,
∴，
当时，，
在Rt△PQD中，,
∴，
得：，
∵当P、Q两个点中有一个点到达终点时，即停止，
∴不成立，
∴；
当时，，如解答图2所示，
此时，QD=，
在Rt△PQD中，,
∴，
解得：；
当时，，解得：，
综上可得：存在，．
（4）当时，∵,易得
∴
∴又∵
∴，
∴．
又∵
∴,
∴,即，
∴
∴．