



专题15 开放探究类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1
展开小丽提出了自己的想法:如图2在线段AB上取一点F,使DA=DF,通过证明△BDF≌△PDA可以解决问题.
(尝试)①请你帮助小丽完成说理过程.
②若AC=6,BC=4,AD=3,求AP的长.
(拓展)如图3,过点A的直线MN∥BC, AB=3 cm,AC=4cm,点D是直线MN上一点,点P是线段AC上的一点,连接DP,使得∠BDP=∠BAC,求的值.
2.(2021·福建省厦门第六中学九年级三模)在△ABC中,AC=BC,∠ACB=90°,点P为△ABC外一点,点P与点C位于直线AB异侧,连接AP,∠APB=45°,过点C作CD⊥PA,垂足为D.
(1)当∠ABP=90°时,直接写出线段AP与CD的数量关系为AP=_____________;
(2)如图,当∠ABP>90°时.
①试探究(1)中的结论是否成立;
②在线段AP上取一点K,使得∠ABK=∠ACD,画出图形并直接写出的值.
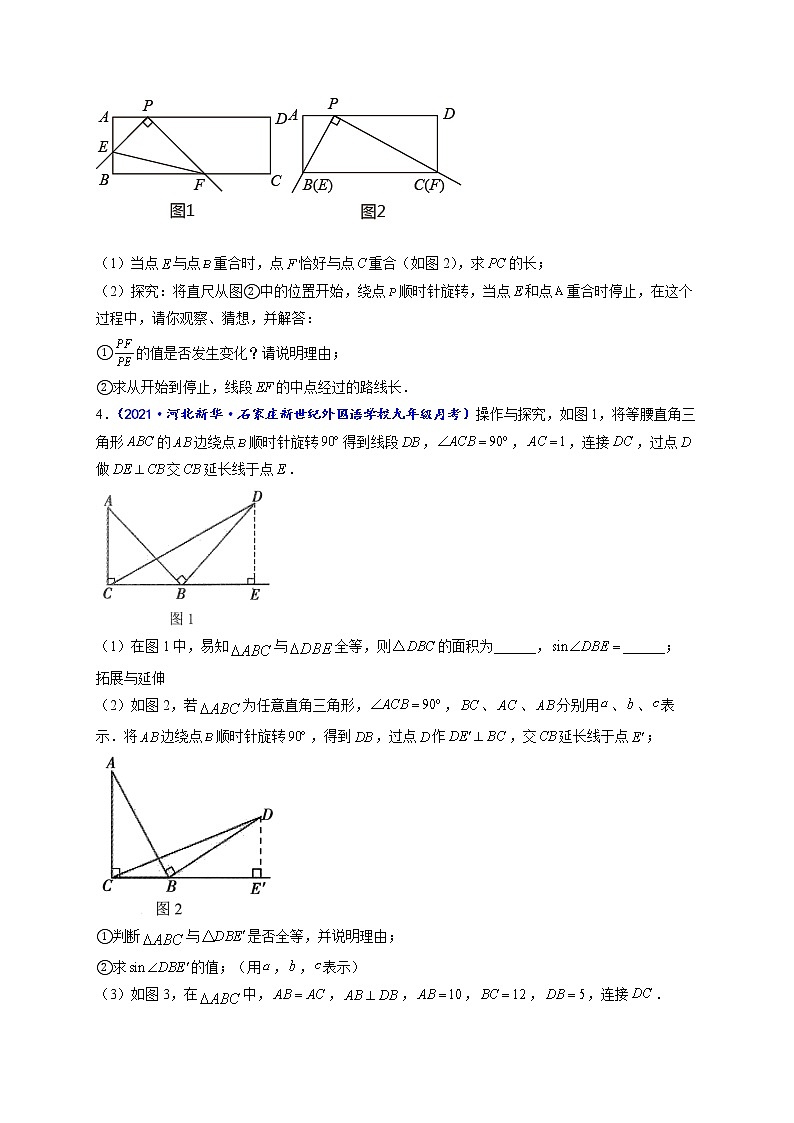
3.(2021·福建涵江·九年级期末)矩形中,点在上,,.将直角尺的顶点放在处直角尺的两边分别交,于点,,连接(如图1).
(1)当点与点重合时,点恰好与点重合(如图2),求的长;
(2)探究:将直尺从图②中的位置开始,绕点顺时针旋转,当点和点重合时停止,在这个过程中,请你观察、猜想,并解答:
①的值是否发生变化?请说明理由;
②求从开始到停止,线段的中点经过的路线长.
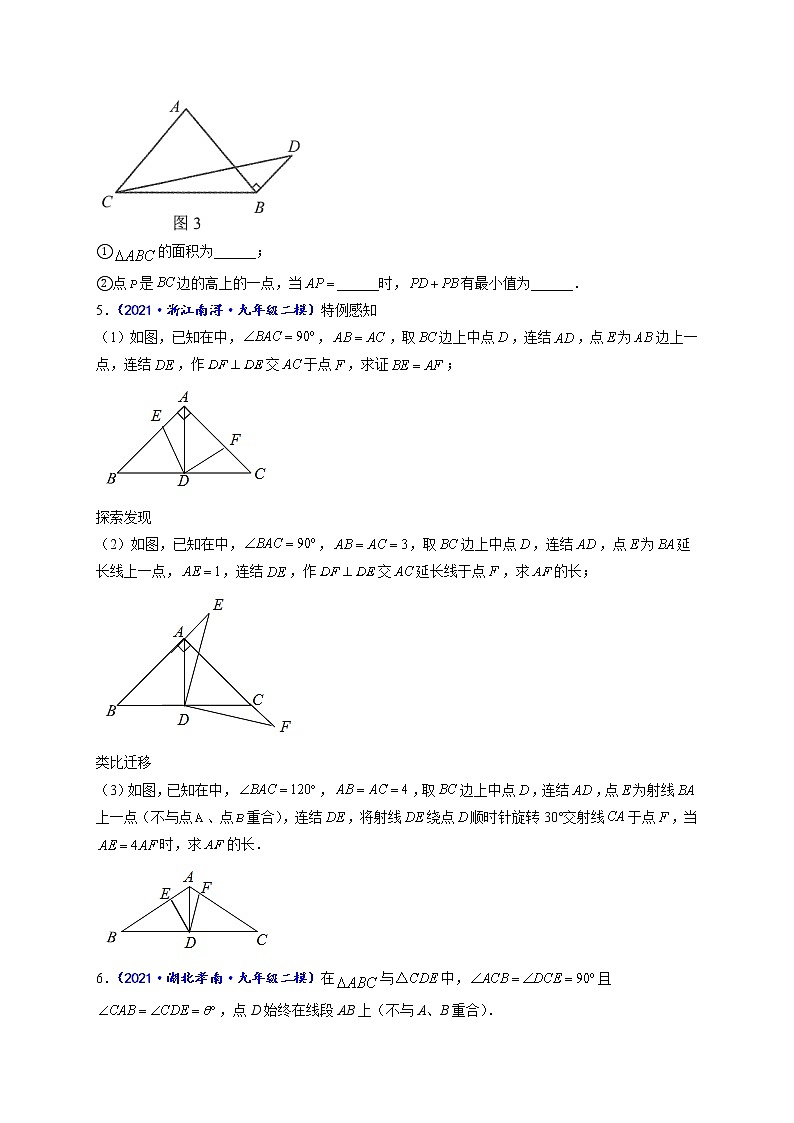
4.(2021·河北新华·石家庄新世纪外国语学校九年级月考)操作与探究,如图1,将等腰直角三角形的边绕点顺时针旋转得到线段,,,连接,过点做交延长线于点.
(1)在图1中,易知与全等,则的面积为______,______;
拓展与延伸
(2)如图2,若为任意直角三角形,,、、分别用、、表示.将边绕点顺时针旋转,得到,过点作,交延长线于点;
①判断与是否全等,并说明理由;
②求的值;(用,,表示)
(3)如图3,在中,,,,,,连接.
①的面积为______;
②点是边的高上的一点,当______时,有最小值为______.
5.(2021·浙江南浔·九年级二模)特例感知
(1)如图,已知在中,,,取边上中点,连结,点为边上一点,连结,作交于点,求证;
探索发现
(2)如图,已知在中,,,取边上中点,连结,点为延长线上一点,,连结,作交延长线于点,求的长;
类比迁移
(3)如图,已知在中,,,取边上中点,连结,点为射线上一点(不与点、点重合),连结,将射线绕点顺时针旋转30°交射线于点,当时,求的长.
6.(2021·湖北孝南·九年级二模)在与中,且,点D始终在线段AB上(不与A、B重合).
(1)问题发现:如图1,若度,的度数______,______;
(2)类比探究:如图2,若度,试求的度数和的值;
(3)拓展应用:在(2)的条件下,M为DE的中点,当时,BM的最小值为多少?直接写出答案.
7.(2021·河南信阳·九年级一模)在中,于点,点为射线上任一点(点除外)连接,将线段绕点顺时针方向旋转,,得到,连接.
(1)(观察发现)如图1,当,且时,BP与的数量关系是___________,与的位置关系是___________.
(2)(猜想证明)如图2,当,且时,(1)中的结论是否成立?若成立,请予以证明;若不成立,请说明理由.(请选择图2,图3中的一种情况予以证明或说理)
(3)(拓展探究)在(2)的条件下,若,,请直接写出的长.
8.(2021·山西洪洞·九年级二模)综合与实践.
问题情境:
综合与实践课上,同学们开展了以“图形的旋转”为主题的数学活动.
实践操作:
如图1,将等腰Rt△AEF绕正方形ABCD的顶点A逆时针方向旋转,其中∠AEF=90,EA=EF,连接CF,点H为CF的中点,连接HD,HE,DE,得到△DHE.
应用探究:
(1)勤奋组:
如图2,当点E恰好落在正方形ABCD的对角线AC上时,判断△DHE的形状,并说明理由;
(2)善思组:
如图3,当点E恰好落在正方形ABCD的边AB上时,(1)中的结论还成立吗?请说明理由;
深入探究:
(3)创新小组:
发现若连接BE,在旋转Rt△AEF的过程中,为定值,请你直接写出其值 .
9.(2021·山西九年级二模)综合与探究
如图1,在平面直角坐标系中,抛物线与轴交于两点(点在点的左侧),与轴交于点,是轴负半轴上一点,,直线与抛物线交于点.
(1)求直线的函数表达式.
(2)如图2,在线段上有一条2个单位长度的动线段(点在点的左侧),过点作轴的垂线,交抛物线于点,交直线于点;过点作轴的垂线,交抛物线于点,交直线于点,连接,.设点的横坐标为,请解答下列问题:
①线段的长为______;(用含的代数式表示)
②当时,判断四边形的形状,并说明理由;
③求当为何值时,.
(3)如图3,当点在抛物线的对称轴上时,连接.试探究:此时在第一象限内是否存在点,使以,,为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.
10.(2021·湖北曾都·九年级期末)定义:在一个三角形中,如果一个内角是另一内角的倍,我们称这样的三角形为“倍角三角形”,把这个倍角的平分线(线段)称为这个三角形的“伴线”.
在倍角中,的平分线就是它的“伴线”,用分别表示的对边.现在我们探究之间存在的数量关系.
(1)(特例探究)(补全填空)
如图1,若,易求得的值为的值为;
如图2,若,易求得的值为 ;的值为 ;
(2)(猜想论证)
根据猜想之间存在怎样的数量关系?请从下列思路中选择一种证明你的猜想.
思路一:如图3,延长至使连接.
思路二:如图4,作的平分线交于点.
(3)(素养提升)
若在这个倍角中,已知且它的三边长恰好是三个连续的正整数,请根据中的结论直接写出这个三角形的“伴线”长.
11.(2020·吉林农安县第三中学、农安三中九年级月考)(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),.易证:∽.
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),.
(1)求证:∽ ;
(2)若PD=4,PC=8,BC=6,求AP的长.
(应用)如图③,在中,AC=BC=8,AB=12,点P在边AB上(点P不与点A、B重合),连结CP,作PE与边BC交于点E.当CE=3EB时,求AP的长.
12.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在平行四边形中,点是的中点,点是线段上一点,的延长线交射线于点.若,求的值.
(1)尝试探究
在图1中,过点作交于点,则和的数量关系是_________,和的数量关系是_________,的值是_________.
(2)类比延伸
如图2,在原题的条件下,若,则的值是_________(用含有的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形中,,点是的延长线上的一点,和相交于点.若,,,则的值是________(用含、的代数式表示).
13.(2020·四川邛崃·九年级期中)几何探究题
(1)发现:在平面内,若,,其中.
当点A在线段BC上时,线段AC的长取得最小值,最小值为 ;
当点A在线段CB延长线上时,线段AC的长取得最大值,最大值为 .
(2)应用:点A为线段BC外一动点,如图2,分别以AB、AC为边,作等边△ABD和等边△ACE,连接CD、BE.
①证明:;
②若,,则线段BE长度的最大值为 .
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为,点B的坐标为,点P为线AB外一动点,且,,.请直接写出线段AM长的最大值及此时点P的坐标.
14.(认识新知)对角线互相垂直的四边形叫做垂美四边形.
(概念理解)(1)如图1,在四边形ABCD中,,,问四边形ABCD是垂美四边形吗?请说明理由;
(性质探究)(2)如图2,四边形ABCD的对角线AC、BD交于点O,.
若OA=1,OB=5,,OC=7,OD=2,则________;________;
求证:;
(解决问题)(3)如图3,中,,且,且,连结CE、BG、则________.
15.(2021·广西九年级二模)如图,在,,,过A作于D,点E为直线上的一动点,把线段绕点E顺时针旋转α,得到线段EF,连接,,直线与相交于点G,与交于点M.
(1)(发现)如图1,当时,填空:
①的值为__________;
②∠AGB的度数为__________;
(2)(探究)如图2,当时,请写出的值及的度数,并就图2的情形给出证明;
(3)(应用)如图3,当时,若﹐,请直接写出的面积.
专题17 规律探究类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题17 规律探究类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题17规律探究类的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题17规律探究类的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
专题16 新定义问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题16 新定义问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题16新定义问题的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题16新定义问题的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
专题14 阅读理解类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题14 阅读理解类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题14阅读理解类的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题14阅读理解类的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。












