



专题18 与一次函数、反比例函数有关的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1
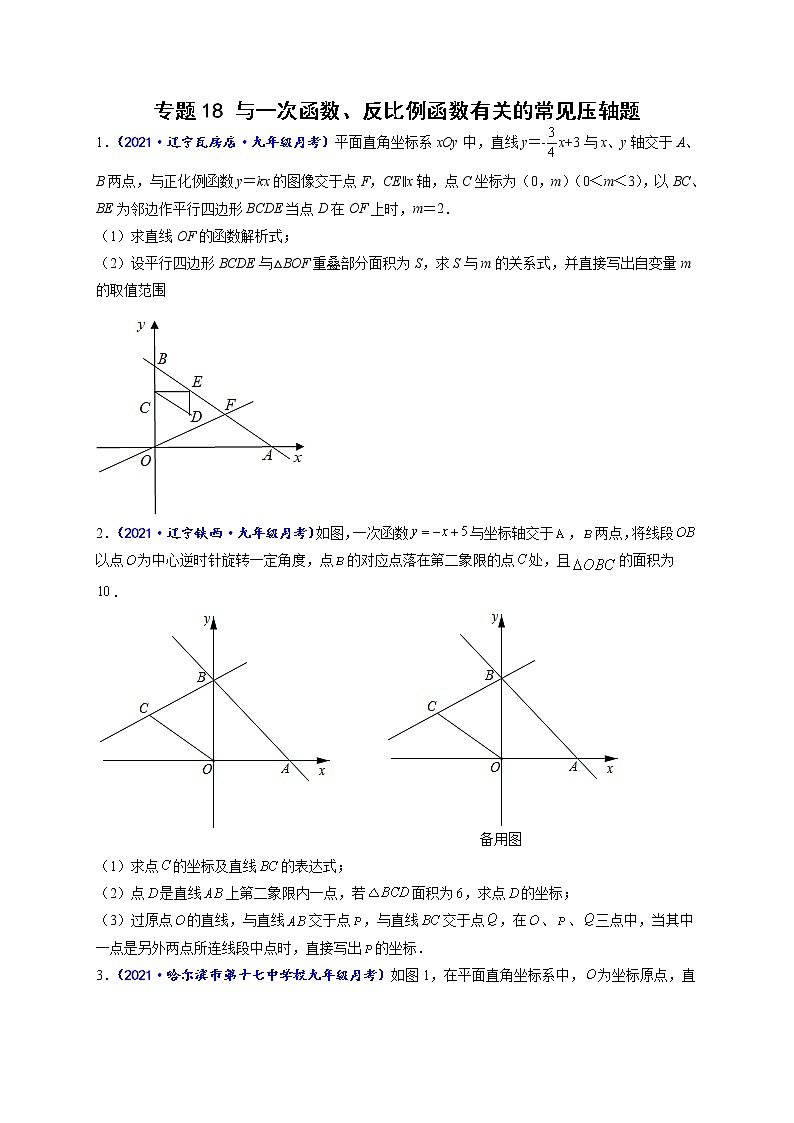
展开(2)设平行四边形BCDE与△BOF重叠部分面积为S,求S与m的关系式,并直接写出自变量m的取值范围
【答案】(1)直线DF的解析式为;(2)
【解题思路分析】(1)利用平行四边形的性质结合一次函数的图象与性质求出点D的坐标即可解决问题;
(2)分三种情况进行分别探究,即①当时,②当时,③当时,分别画出相应的图形,求出相应的边的长用含有m的代数式表示,再表示面积,从而确定在不同情况下S与m的函数解析式.
【解析】解:(1)∵直线y=﹣x+3与x、y轴交于A、B两点,
∴令,则;令,则,解得,
∴点A的坐标为(4,0),点B的坐标为(0,3)
∵
∴C(0,2)
∴OC=2
∴
∵四边形BCDE是平行四边形,
∴DE=BC=1
∵轴
∴点E的纵坐标为2
∴
∴
∴,
∴
∵点D在直线y=kx上
∴,即
∴直线DF的解析式为
(2)联立,
解得,
①当时,如图1,
∵轴
∴,即CE为OB边上的高,
∴
把代入 y=﹣x+3得:
∴,
∴
②当时,设CD,ED分另交OF于点H,P,如图2,
由①知,
把代入得:
∴
∵
∴
∴
∵,且
∴直线DC为
∵H为CD与OF的交点,
∴
∴
∴点H与PD之间的距离d=
∴
=
∴
③当时,CD,CE分另交OF于点H,P,如图3,
由②可得
∴
∵直线OF与AB相交于点F
∴
∴
∴
∴
综上,
2.(2021·辽宁铁西·九年级月考)如图,一次函数与坐标轴交于,两点,将线段以点为中心逆时针旋转一定角度,点的对应点落在第二象限的点处,且的面积为.
(1)求点的坐标及直线的表达式;
(2)点是直线上第二象限内一点,若面积为,求点的坐标;
(3)过原点的直线,与直线交于点,与直线交于点,在、、三点中,当其中一点是另外两点所连线段中点时,直接写出的坐标.
【答案】(1),;(2);(3)①当点是中点时,点的坐标为,②当点是中点时,点的坐标为;③当点是中点时,点的坐标为.
【解题思路分析】(1)由的面积,求出,由,求出的值,确定点坐标,之后可以求得直线的表达式;
(2)过点作轴于,过点作轴于,连接,这样用四边形的面积减去和的面积,即可得出结论;
(3)设出点的坐标,表示出直线的解析式,与直线联立,确定点的坐标,分别以点是中点、点是中点、点是中点三种情况,利用中点坐标公式列方程求解.
【解析】解:(1)∵一次函数与坐标轴交于,两点,
故点,的坐标分别为、,
∴,
则的面积=,
解得,
设点的坐标为,且由已知可得,
∴,
解得,
∴点的坐标为,
设的表达式为,且,,
∴,
解得,
∴直线的表达为;
(2)过点作轴于,过点作轴于,连接,
∴四边形为梯形,
由(1)可得 ,
∴ ,,,
∴ ,
∵在直线上, ,
∴设且在第二象限,
∴ ,
∴ ,
∵,
∴,
,
∴解得 ,
∴ ,
∴;
(3)设点的坐标为,
则的表达式为,
联立上式与并解得,
即点的横坐标为,
①当点是中点时,
则点、的横坐标互为相反数,
即,
解得(舍去)或,
故点的坐标为,
②当点是中点时,
可得:,
解得(舍去)或,
故点的坐标为;
③当点是中点时,
可得
解得(舍去)或,
故点的坐标为.
综上所述,点坐标为,,
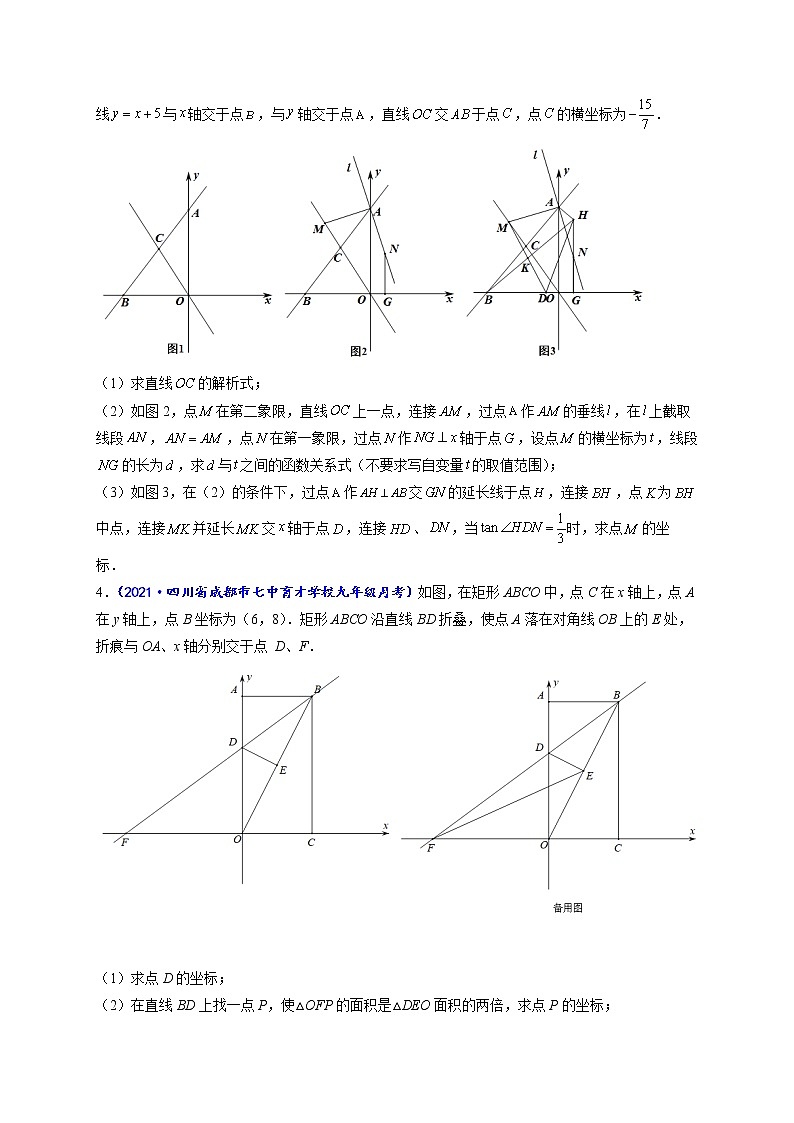
3.(2021·哈尔滨市第十七中学校九年级月考)如图1,在平面直角坐标系中,为坐标原点,直线与轴交于点,与轴交于点,直线交于点,点的横坐标为.
(1)求直线的解析式;
(2)如图2,点在第二象限,直线上一点,连接,过点作的垂线,在上截取线段,,点在第一象限,过点作轴于点,设点的横坐标为,线段的长为,求与之间的函数关系式(不要求写自变量的取值范围);
(3)如图3,在(2)的条件下,过点作交的延长线于点,连接,点为中点,连接并延长交轴于点,连接、,当时,求点的坐标.
【答案】(1);(2)=5+t;(3)M(-3,4)
【解题思路分析】(1)先利用求出点C的坐标,再利用待定系数法求解;
(2)过点M作MR⊥y轴于R,过点N作NS⊥y轴于S,则,证明△AMR≌△NAS,得到SN=AR=,得到点N的坐标,即可得到关系式;
(3)求出点H,K,D的坐标,得到DG、HG、HN、DG、DH的长,过点N作NP⊥DH于P,证明△HPN∽△HGD,,求出PN、HP、PD,根据代入计算求出t的值,由此得到点M的坐标.
【解析】解:(1)将x=代入中,得,
∴C(),
设直线OC的解析式为y=kx,将点C坐标代入,得,
解得,
∴直线的解析式为;
(2)∵点在第二象限,直线上一点,点的横坐标为,
∴点的坐标为(),
如图,过点M作MR⊥y轴于R,过点N作NS⊥y轴于S,则,
∴
∵AM⊥AN,
∴
∴
∴
又∵AM=AN,
∴△AMR≌△NAS,
∴AS=MR=-t,SN=AR=,
∴点N的坐标为(,5+t),
∵轴,
∴线段的长为=5+t;
(3)∵AH⊥AB,直线AB的解析式为,
∴AH的解析式为y=-x+5,
∴点H的坐标为(),
∵点B的坐标为(-5,0),
∴直线BH的中点K的坐标为(),
∴直线MK的解析式为,
∴D(),
∵H(),G(),N(,5+t),
∴,,,
∴,
过点N作NP⊥DH于P,则,
∴△HPN∽△HGD,
∴,
∴,
解得,
,
∴,
∵,
∴PD=3PN,
∴,
解得t=-5,或t=-3,
∴M()(不合题意,舍去)或M(-3,4).
4.(2021·四川省成都市七中育才学校九年级月考)如图,在矩形ABCO中,点C在x轴上,点A在y轴上,点B坐标为(6,8).矩形ABCO沿直线BD折叠,使点A落在对角线OB上的E处,折痕与OA、x轴分别交于点 D、F.
(1)求点D的坐标;
(2)在直线BD上找一点P,使△OFP的面积是△DEO面积的两倍,求点P的坐标;
(3)连接EF,在第二象限是否存在点G,使得△EFG是等腰直角三角形.若存在,请直接写出点G的坐标;若不存在,请说明理由.
【答案】(1)D(0,5);(2)P(-,)或(-,-);(3)存在,点G坐标为(-,)或(-,)或(-,).
【解题思路分析】(1)由勾股定理可求OB=10,由折叠的性质可得AB=BE=6,AD=DE,∠BAO=∠DEB=90°,利用勾股定理可求解;
(2)先求出BD解析式,可求点F坐标,由三角形的面积公式可求点P坐标;
(3)利用三角形的面积公式可求点E坐标,分三种情况讨论,利用全等三角形的性质和等腰直角三角形的性质可求解.
【解析】解:(1)∵矩形ABCO中,点B坐标为(6,8),
∴AB=OC=6,AO=BC=8,
∴OB==10,
∵矩形ABCO沿直线BD折叠,
∴AB=BE=6,AD=DE,∠BAO=∠DEB=90°,
∴OE=4,
∵OD2=DE2+OE2,
∴OD2=(8-OD)2+42,
∴OD=5,
∴点D(0,5);
(2)∵点D(0,5),点B(6,8),
∴直线BD解析式为:y=x+5,
当y=0时,x=-10,
∴点F(-10,0),
∴OF=10,
∵OD=5,
∴AD=3,
∴S△DEO=S△ABO-2S△ADB=24-2××3×6=6,
∴S△OFP=2×6=12,
设点P(a,a+5),
∴×10×|a+5|=12,
∴a1=-,a2=-,
∴点P(-,)或(-,-);
(3)存在,理由如下:
如图1,过点E作EH⊥AO于H,
∵S△DEO=×OD×HE=6,
∴HE=,
∴OH==,
∴点E(,),
如图2,当∠GFE=90°,GF=EF时,过点G作GN⊥x轴于N,过点E作EM⊥x轴于M,
∴EM=,OM=,
∴FM=,
∵∠GFE=90°=∠GNF=∠FME,
∴∠NFG+∠NGF=∠NFG+∠EFM=90°,
∴∠EFM=∠NGF,
又∵GF=EF,
∴△GFN≌△FEM(AAS),
∴NF=EM=,GN=FM=,
∴ON=,
∴点G(-,);
当∠FG''E=90°,EG''=FG''时,
∴点G''是GE的中点,
∴点G''的坐标为(-,);
当∠FEG'=90°,EF=EG'时,
∴点G''是FG'的中点,
∴点G'坐标为(-,),
综上所述:点G坐标为(-,)或(-,)或(-,).
5.(2021·北京市第五中学分校九年级月考)在平面直角坐标系xOy中,正方形MNPQ中M(1,1),N(﹣1,1),P(﹣1,﹣1),Q(1,﹣1).给出如下定义:记线段AB的中点为G,当点G不在正方形MNPQ上时,平移线段AB,使点G落在正方形MNPQ上,得到线段A′B′(A′,B′分别为点A,B的对应点)线段AA′长度的最小值称为线段AB到正方形MNPQ的“平移距离”.
(1)已知点A的坐标为(﹣1,0),点B在x轴上;
①若点B与原点O重合,则线段AB到正方形MNPQ的“平移距离”为 ;
②若线段AB到正方形MNPQ的“平移距离”为2,则点B的坐标为 ;
(2)若点A,B都在直线y=x+4上,AB=2,记线段AB到正方形MNPQ的“平移距离”为d1,求d1的最小值;
(3)若点A的坐标为(4,4),AB=2,记线段AB到正方形MNPQ的“平移距离”为d2,直接写出d2的取值范围.
【答案】(1)①,②(-5,0)或(7,0);(2) ;(3).
【解题思路分析】(1)①由题意可直接得出G的坐标为,即得出移动最小距离为;
②根据题意可知AB中点G在x轴上.即可分类讨论Ⅰ当B点在A点左侧时,即G点也在A点左侧时,由平移距离的定义可知NP与x轴的交点即点A到的距离为2,即可得出
B点坐标;Ⅱ当B点在A点右侧时,即G点也在A点右侧时, 由平移距离的定义可知MQ与x轴的交点到点的距离为2,即可得出B点坐标.
(2)由题意可知点N到直线的距离即为的最小值,由N点向直线所做垂线与直线的交点即为G点.易求出GN的解析式为.联立两个函数解析式,即可求出G点坐标,即求出GN的长度,即为.
(3)由题意可知点B是以A为圆心,半径为2的圆上的点,即得出点G是以A为圆心,半径为1的圆上的点,由,,即可求出的取值范围.
【解析】(1)①如图,当B与原点O重合时,AB中点G的坐标为,
∴移动最小距离为向左平移到NP与x轴交点上.
②由点A,B点在x轴上可知:AB中点G也在x轴上.
Ⅰ当B点在A点左侧时,即G点也在A点左侧时,如图,
由平移距离的定义可知NP与x轴的交点,即点A到的距离为2,
∴,
∴
∵G为AB中点,
∴
∴,
∴B点坐标为(-5,0).
Ⅱ当B点在A点右侧时,即G点也在A点右侧时,如图,
由平移距离的定义可知MQ与x轴的交点到点的距离为2,
∴
∴
∴
∵G为AB中点,
∴
∴,
∴B点坐标为(7,0).
综上可知B点坐标为(-5,0)或(7,0).
(2)由题意作出图形如下:
∴点N到直线的距离即为的最小值,由N点向直线所做垂线与直线的交点即为G点.
∴设直线GN的解析式为,
∵N(-1,1)
∴,解得:
故直线GN的解析式为.
联立,解得:,
∴G点坐标为,
∴
(3)如图,由题意可知点B是以A为圆心,半径为2的圆上的点,
∴点G是以A为圆心,半径为1的圆上的点,
∴,
∵,
∴,
∴
6.(2021·长春市第一零九中学九年级月考)在平面直角坐标系中,函数y=﹣ax+1(x>a)的图像记为M1,函数y=ax+1(x≤a)的图像记为M2,图像M1和M2合起来记为图像M.
(1)当a=1时
①若点P(﹣2,b)在图像M上,求b的值.
②求图像M与x轴的交点坐标.
③直接写出﹣2≤x≤3时,y的最大值和最小值.
(2)当图像M上存在1个或3个点到x轴距离为2时,直接写出a的取值范围.
(3)已知矩形ABCD的四个端点坐标分别为A(﹣2,a),B(3,a),C(3,﹣a),D(﹣2,﹣a),当图像M与矩形ABCD恰有2个公共点时,直接写出a的取值范围.
【答案】(1)①;②;③﹣2≤x≤3时,y的最大值为,最小值为;(2)或;(3)或者或者.
【解题思路分析】(1)①将代入解析式,进而根据的解析式求得的值;
②根据①中的解析式,令,进而求得图像M与x轴的交点坐标;
③分类讨论当时,求得的最大值和最小值,当时,求得的最小值,进而求得﹣2≤x≤3时,y的最大值和最小值;
(2)分类讨论,分图像M上存在1个点和3个点到x轴距离为2时两种情况讨论,当存在3个点时,根据当()时,且,当存在1个点时,根据当()时,且,分别列出不等式组,解不等式即可求的出a的取值范围;
(3)当图像M与矩形ABCD恰有2个公共点时,分三种情况讨论,①当,且与矩形有2个交点时,当在下方时, 且;②当,且与矩形有2个交点时当过点上方时,即,且与矩形有2个交点,即时,,③当且有2个交点时,当时,,且,,分别列出不等式组,解不等式即可求的出a的取值范围.
【解析】(1)根据题意,当时,的解析式为,的解析式为:;
的解析式为
①若点P(﹣2,b)在图像M上,
点在上,
将代入,解得
②时,,则与轴无交点
由的解析式为:;
令,解得
与x轴的交点坐标为
③如图,当时,由的图象可知,随的增大而增大,
的最小值为时,,
的最大值为时,,
当时,由的图象可知,随的增大而减小,
则不存在最大值,
的最小值为当时,
综上所述,﹣2≤x≤3时,y的最大值为,最小值为.
(2)①当图像M上存在3个点到x轴距离为2时,如图,
当()时,且
即,
解得 ,
,
②当图像M上存在1个点到x轴距离为2时,如图,
当()时,且,
即,
解得,
,
综上所述,当图像M上存在1个或3个点到x轴距离为2时,或;
(3)当图像M与矩形ABCD恰有2个公共点时,分三种情况讨论,
矩形ABCD的四个端点坐标分别为A(﹣2,a),B(3,a),C(3,﹣a),D(﹣2,﹣a),
①当,且与矩形有2个交点时,如图,
当在下方时, 且
即
解不等式,即,
恒成立,
取任何实数,
解不等式,
即,
令 ,
解得,
,
,
,
则或
解得或,
,
,
的解集为,
②如图,当,且与矩形有2个交点时当过点上方时,即,且与矩形有2个交点,即时,,
即,
解得,
,
③当且有2个交点时,
,,
当时,,且,如图,
即,
即,
解不等式,
,
或,
解得(舍),,
解不等式,即,
恒成立,
取任何实数,
的解集为.
综上所述,当图像M与矩形ABCD恰有2个公共点时,或者或者.
7.(2021·北京北师大实验中学九年级开学考试)在平面直角坐标系中,点,点在轴的负半轴上.若点,在线段上,且为某个一边与轴平行的矩形的对角线,则称这个矩形为点,的“伴随矩形”.下图为点,的“伴随矩形”的示意图.
(1)若点,点的横坐标为,则点,的“伴随矩形”的面积为 ;
(2)点,的“伴随矩形”是正方形.
①当正方形面积为4,且点到轴的距离为3时,写出点的坐标,并求出直线的函数解析式;
②当正方形的对角线长度为时,原点与所有正方形上各点所连线段的长记为,直接写出的取值范围.
【答案】(1)8;(2)①,的解析式为或;②
【解题思路分析】(1)确定BC的解析式求出点C坐标即可解决问题;
(2)①根据题意确定点N的坐标即可解决问题;
②由正方形MENF的对角线为,推出点F的运动轨迹是直线l′:y=x+9,点E的运动轨迹是直线l:y=x+3,作OP⊥直线l于P交直线l′于Q.求出OP,OQ即可解决问题.
【解析】解:(1)如图1中,
设直线的解析式为
把,代入得
解得
直线的解析式为,
当时,,
,
,的“伴随矩形”矩形的长为4,宽为2,面积为8.
故答案为8.
(2)①如图2中,
点,的“伴随矩形”是正方形,
,
由图可得,或,
设直线的解析式为y=mx,把或代入得1=-5m或-5=m
解得m=或m=-5
直线的解析式为或.
②如图3中:
正方形的对角线为,
由图可得点的运动轨迹是直线,点的运动轨迹是直线,
作直线于交直线于.可得,,
当点与重合时,点,此时的值最大,最大值,
原点与所有正方形上各点所连线段中的最大值为,最小值为,
.
8.(2021·重庆巴蜀中学九年级月考)如图,已知直线与双曲线交于两点,且点坐标为().
(1)求双曲线解析式及点坐标;
(2)将直线向下平移一个单位得直线,是轴上的一个动点,是上的一个动点,求的最小值;
(3)若点为轴上的一个动点,为平面内一个动点,当以、、为顶点的四边形是矩形时,直接写出点坐标.
【答案】(1),B(-2,-1);(2)AP+PQ 的最小值为;(3).
【解题思路分析】(1)把的坐标代入求解的值,再求解反比例解析式为 再联立两个函数解析式,解方程组可得的坐标;
(2)如图,作关于y轴的对称点,过作于,交轴于 则取得最小值,此时 再先求解 再利用等腰直角三角形的性质可得答案;
(3)分两种情况讨论,如图,当为边时,当为矩形的对角线时,再利用矩形的性质及勾股定理与中点坐标公式建立方程,解方程可得答案.
【解析】解:(1)把点坐标为()代入得:
则
.
双曲线为
解得:或
(2)如图,作关于y轴的对称点,过作于,交轴于 则取得最小值,此时
将直线向下平移一个单位得直线,
的解析式为: 且是第一,第三象限的角平分线组成的,
所以最小值为;
(3)如图,当为边时,设
四边形为矩形,
则由平移的性质可得:
同理可得:
则
由平移的性质可得:
如图,当为矩形的对角线时,设
由矩形的性质:对角线相等且互相平分,再结合中点坐标可得,
解得:
综上:.
9.(2021·沙坪坝·重庆一中九年级开学考试)如图1,在平面直角坐标系xOy中,双曲线与直线交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知,A点坐标为.
(1)求一次函数与反比例函数的解析式;
(2)如图2,将线段DO沿y轴平移得线段,在移动过程中,是否存在某个位置使的值最大?若存在,求出的最大值及此时点的坐标;若不存在,请说明理由;
(3)如图3,在x轴取一点,将直线OA沿x轴正半轴平移,平移过程中在第一象限交的图象于点M(M可与A重合),交x轴于点N.在平移过程中,是否存在某个位置使以M、N、E和平面内某一点P为顶点的四边形为菱形且以MN为菱形的边?若存在,请直接写出P的坐标;若不存在,请说明理由.
【答案】(1)y=x+,;(2)的最大值为,此时点O’(0,);(3)(,)或(8,4).
【解题思路分析】(1)先求出点C的坐标,再根据待定系数法,即可求解;
(2)把A向下平移个单位得A′(3,),作B关于y轴的对称点B′,则四边形AA’O’D’是平行四边形,则有=|B′O’−A′O’|=B′O’−A′O’≤A′B′,想办法求出A′B′,直线A′B′,的解析式即可解决问题.
(3)设设M(m,),则N(m−,0),NE2=(5−m+)2,ME2=(5−m)2+()2,MN2=()2+()2,分MN=EM,MN=NE两种情形,分别构建方程即可解决问题.
【解析】解:(1)∵A(3,4),
∴OA=,
∵OA=OC,
∴OA=OC=5,
∴C(−5,0),
把A、C两点坐标代入y=ax+b得到:,解得:,
∴直线的解析式为y=x+,
把A(3,4)代入中,得到k=12,
∴反比例函数的解析式为;
(2)把x=0代入y=x+,可得:y=,即:OD=,
把A向下平移个单位得A′(3,),作B关于y轴的对称点B′,则四边形AA’O’D’是平行四边形,
则有=|B′O’−A′O’|=B′O’−A′O’≤A′B′,
联立y=x+,可得:或
∴B(−8,),B′(8,),
∴A’B’=
直线A’B’:y=x+,
令x=0,可得y=,
∴O’(0,).
∴的最大值为,此时点O’(0,);
(2)设M(m,),
∵AO∥MN,
∴∠AOE=∠MNE,即:tan∠AOE=tan∠MNE=,
∴N(m−,0),NE2=(5−m+)2,ME2=(5−m)2+()2,MN2=()2+()2
假设存在某个位置使以M、N、E和平面内某一点P为顶点的四边形为菱形且以MN为菱形的边,
①当MN=ME,即(5−m)2+()2=()2+()2,解得m=或(舍去)
经检验:m=是方程的解,
∴M(,),N(5,0),此时点N,E重合,不符合题意舍去,
②当MN=NE,即(5−m+)2=()2+()2,解得m=8或3或-3(舍去)或2(舍弃),
经检验:m=8或3是方程的解,
∴M(8, )或(3,4),此时N(,0)或(0,0),
∴NE=-5=或5,
∴P(8-,)或(3+5,4),即:P(,)或(8,4),
综上所述,满足条件的点P的坐标为(,)或(8,4).
10.(2021·江苏常州·中考真题)通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.
(理解)
(1)如图1,,垂足分别为C、D,E是的中点,连接.已知,.
①分别求线段、的长(用含a、b的代数式表示);
②比较大小:__________(填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
(应用)
(2)如图2,在平面直角坐标系中,点M、N在反比例函数的图像上,横坐标分别为m、n.设,记.
①当时,__________;当时,________;
②通过归纳猜想,可得l的最小值是__________.请利用图2构造恰当的图形,并说明你的猜想成立.
【答案】(1)①,=;②>,>;(2)①,1;②l的最小值是1,理由见详解
【解题思路分析】(1)①先证明,从而得,进而得CD的值,根据直角三角形的性质,直接得CE的值;②根据点到线之间,垂线段最短,即可得到结论;
(2)①把m,n的值直接代入=进行计算,即可;②过点M作x,y轴的平行线,过点N作x,y轴的平行线,如图所示,则A(n,),B(m,),画出图形,用矩形的面积表示,进而即可得到结论.
【解析】解:(1)①∵,
∴∠ACD+∠A=∠ACD+∠BCD=90°,即:∠A=∠BCD,
又∵∠ADC=∠CDB=90°,
∴,
∴,即:,
∴,即:(负值舍去),
∵E是的中点,
∴==;
②∵,,
∴>,即:>.
故答案是:>;
(2)①当时,==,
当时,==,
故答案是:,1;
②l的最小值是:1,理由如下:
由题意得:M(m,),N(n,),过点M作x,y轴的平行线,过点N作x,y轴的平行线,如图所示,则A(n,),B(m,),
==
=[(①的面积+②的面积)+②的面积+(②的面积+④的面积)+(①的面积+②的面积+③的面积 +④的面积)]
= [(①的面积+②的面积)+(②的面积+④的面积)+(①的面积+②的面积)+(②的面积+④的面积)+③的面积]
=(1+1+1+1+③的面积)≥1,
∴l的最小值是1.
11.(2021·哈尔滨市第一一三中学校九年级月考)如图,在平面直角坐标系中,直线交x轴于点B,交y轴于点A,OA=OB=2.
(1)求直线AB的解析式;
(2)如图,点C在OA的延长线上,点D在x轴的正半轴上,连接CD交直线AB于点E,点E为线段CD的中点,设点D的横坐标为t,△CAE的面积为S,求S与t的函数解析式;
(3)如图,在(2)的条件下,过点E作EF⊥x轴于点F,点M为EB的中点,过M作MH⊥CD于点H,延长HM交x轴于点G,点N在AB的延长线上,连接NG、DN、CM,若FG=OC,∠ACM=∠GDN,求GN的长.
【答案】(1);(2);(3)
【解题思路分析】(1)根据OA、OB的长度写出点坐标,将A、B点坐标代入解析式中即可求出答案;
(2)利用E是CD的中点,写出E点横坐标,再利用点E在直线AB上,将E点横坐标代入求出纵坐标,继而表示出点C的纵坐标坐标,最后即可表示出与的函数解析式;
(3)由题意可知,再根据已知条件表示出各点的坐标以及直线CD和GM的k值,最后利用垂直关系求解即可.
【解析】解:(1)∵直线交x轴于点B,交y轴于点A,,
∴,,
将A、B两点代入中,
得:,
解得:,
∴直线AB的解析式为;
(2)∵点D的横坐标是t,且E是CD的中点 ,
∴点E的横坐标为,
∵点E在直线AB上,
∴将E的横坐标为代入中,得,
∴点C的纵坐标为,
∴,
∴与的函数解析式为;
(3)由题可知:,, ,,,
∵点M是BE的中点,
∴,
∵,
∴,
∴,
∴
∴, ,
∵,即,
∴,即,
整理得:,
解得:,,
∵点D在x轴正半轴上,
∴,
∴,
∴,,
又∵,,
∴,
∵,
∴,
∴,
又∵,
∴,
∴
∵点N在直线AB上,
∴将代入中,
得,
∴,
∴
12.(2021·首都师范大学附属中学九年级月考)对图形M,N和点P,如果图形M上存在点Q1,图形N上存在点Q2,使得点Q1绕点P顺时针旋转90°后与点Q2重合,则称图形N是图形M关于点P的“秋实”图形.
(1)如图1,A(﹣3,0),B(0,3),则点C1(1,0),C2(﹣2,﹣1),C3(3,0)中.是线段AB关于坐标原点O的“秋实”图形的点是 ;
(2)设直线y=x+b(b>0)与x轴负半轴交于点D,与y轴正半轴交于点E,⊙F是以点F(2,1)为圆心,2为半径的圆.若⊙F是线段DE关于坐标原点O的“秋实”图形,求b的取值范围;
(3)设直线l:y=k(x+m),其中m>0,⊙G是以G(4,0)为圆心,1为半径的圆,若对⊙G上的任意一点H,存在k(≤k≤),使得点H是直线l关于坐标原点O的“秋实”图形,请直接写出m的取值范围.
【答案】(1)C3;(2)≤b≤;(3).
【解题思路分析】(1)先理解新定义,利用待定系数法求 AB的解析式为,然后求出点逆时针旋转后的点坐标点C1(1,0)对应点坐标为(0, 1),点C2(-2,-1)对应点坐标为(1,-2),点C3(3,0)对应点坐标为(0, 3),在代入解析式验证即可;
(2)连结OF并延长与圆交于M、N两点,先求出OF=,再求ON=,OM=,点M是圆上最近点,点N是圆上最远点,tan∠IOF= ,cs∠IOF=,求出点M(,),点N(,),点M绕点O逆时针旋转90°点M的对应点坐标(,),点N绕点O逆时针旋转90°点N的对应点坐标(,),点N、M的对应点在直线y=x+b上,代入求出b的值即可;
(3)过点O作⊙G的切线OD、OE,连结DE交x轴于F,连结OD,OE,求出OD=OE=,利用面积求EF=DF=,在Rt△ODF中,求出点D(,),点E(,)逆时针方向旋转90°,点D′(,),点E′(,)分别代入最大与最小k对应解析式求出m即可.
【解析】解:(1)设AB的解析式为,
∵点A(﹣3,0),B(0,3),将坐标代入解析式得
,
解得,
∴AB的解析式为,
点C1(1,0)绕原点O逆时针旋转90°对应点坐标为(0, 1),
点C2(-2,-1)绕原点O顺时针旋转90°对应点坐标为(1,-2),
点C3(3,0)绕原点O顺时针旋转90°对应点坐标为(0, 3),
当x=0时,,C1不是线段AB关于坐标原点O的“秋实”图形的点,
当x=-1时,,C2不是线段AB关于坐标原点O的“秋实”图形的点,
当x=0时,,C3是线段AB关于坐标原点O的“秋实”图形的点,
故答案为C3;
(2)连结OF并延长与圆交于M、N两点,OF=,ON=,OM=,
点M是圆上最近点,OM长最小,点N是圆上最远点,ON长最大,
过M、F、N分别作MG⊥y轴于G,FI⊥y轴于I,NH⊥y轴于H,
∴tan∠IOF= ,cs∠IOF=,
∴OG=OMcs∠IOF=,
∴GM=2OG=,
∴OH=ON cs∠IOF=,
∴NH=2OH=,
点M(,),点N(,),
点M绕点O逆时针旋转90°点M的对应点坐标(,),
点N绕点O逆时针旋转90°点N的对应点坐标(,),
点N、M的对应点在直线y=x+b上,
=+b,
∴b=,
=+b,
∴b=,
∴≤b≤;
(3)过点O作⊙G的切线OD、OE,连结DE交x轴于F,连结OD,OE,
∵OG=4,DG=1,OG⊥OD,
∴OD=OE=,
∴EF=DF=,
在Rt△ODF中,
∴点D(,),点E(,),
逆时针方向旋转90°,点D′(,),点E′(,),
点D′在y=(x+m)上,
∴,
解得,
点E′在直线在y=(x+m)上,
∴,
解得,
∴,
13.(2021·浙江中考真题)已知在平面直角坐标系中,点是反比例函数图象上的一个动点,连结的延长线交反比例函数的图象于点,过点作轴于点.
(1)如图1,过点作轴于点,连结.
①若,求证:四边形是平行四边形;
②连结,若,求的面积.
(2)如图2,过点作,交反比例函数的图象于点,连结.试探究:对于确定的实数,动点在运动过程中,的面积是否会发生变化?请说明理由.
【答案】(1)①证明见解析,②1;(2)不改变,见解析
【解题思路分析】(1)①计算得出,利用平行四边形的判定方法即可证明结论;
②证明∽,利用反比例函数的几何意义求得,即可求解;
(2)点的坐标为,点的坐标为,可知四边形是平行四边形,由∽,利用相似三角形的性质得到关于的一元二次方程,利用三角形的面积公式即可求解.
【解析】(1)①证明:设点的坐标为,
则当时,点的坐标为,
,
轴,
,
∴四边形是平行四边形;
②解:过点作轴于点,
轴,
,
∽,
,
∴当时,则,即.
;
(2)解 不改变.
理由如下:
过点作轴于点与轴交于点,
设点的坐标为,点的坐标为,
则,OH=b,
由题意,可知四边形是平行四边形,
∴OG=AE=a,∠HPG=∠OEG=∠EOA,且∠PHG=∠OEA=90°,
∴∽,
,
即,
∴,
,
解得,
异号,,
,
.
∴对于确定的实数,动点在运动过程中,的面积不会发生变化.
.
14.(2021·湖南茶陵·九年级模拟预测)如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,),反比例函数(x>0)的图象与BC,AB分别交于D,E,BD=.
(1)写出D点坐标,并求出反比例函数关系式;
(2)判断线段DE与AC的位置关系并说明理由;
(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.
【答案】(1)D(),;(2)DE//AC,理由见解析;(3)点G的坐标为或G,都在反比例函数的图象上.
【解题思路分析】(1)先根据图象确定BC的长,再结合BD=,求得CD,J进而确定点D的坐标,最后运用待定系数法求解即可;
(2)根据(1)可得,进而确定点E的坐标,然后求出AE、BE,再证即可完成证明;
(3)分当点F在点C的下方和上方两种情况分别求解即可.
【解析】解:(1)∵B(2,),
∴BC=2,
又∵BD=
∴,D( )
∴
∴
(2)DE//AC,理由如下:
由(1)得,当时,,
∴,,
∵,,
∴
∴DE//AC;
(3)①当点F在点C的下方,且点G在点F的右方时,如下图:
过点F作FH于点H,
∵四边形BCFG是菱形,
∴BC=CF=FG=GB=2,
在中,OA=BC=2,OC=AB=,
∴AC=4,∠ACB=30°,
∴在中,HF=,,
∴OH=,
∴F((,G
当时,,
∴点G在反比例函数的图象上;
②当点F在点C的上方,且点G在点F的右方时,
同理可得:G,点G在反比例函数的图象上.
综上:点G的坐标为或G,都在反比例函数的图象上.
15.(2021·广东南山·九年级期末)如图,在平面直角坐标系中,直线y=3x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数y=(x>0)交于点C,且BC=2AB,BD∥x轴交反比例函数y=(x>0)于点D,连接AD.
(1)求b、k的值;
(2)求△ABD的面积;
(3)若E为射线BC上一点,设E的横坐标为m,过点E作EF∥BD,交反比例函数y=(x>0)的图象于点F,且EF=BD,求m的值.
【答案】(1)b=3,k=18;(2)9;(3)m的值为1或
【解题思路分析】(1)作CH⊥y轴于点H,把点A坐标代入直线解析式中求出b,求出点B坐标,再用相似三角形的性质求出CH、BH,求出点C坐标,即可求出k;
(2)先求出点D坐标,求出BD,根据三角形的面积公式计算,得到答案;
(3)先求出EF=2,设出点E坐标,分0<m<2、m>2两种情况,表示出点F坐标,根据反比例函数图象上点的坐标特征建立方程求解,即可得出结论.
【解析】解:(1)作CH⊥y轴于点H,
∵直线y=3x+b经过点A(﹣1,0),
∴﹣1×3+b=0,
解得,b=3,
对于直线y=3x+3,当x=0时,x=3,
∴点B的坐标为(0,3),即OB=3,
∵CH∥OA,
∴△AOB∽△CHB,
∴,即,
解得,CH=2,BH=6,
∴OH=OB+BH=9,
∴点C的坐标为(2,9),
∴k=2×9=18;
(2)∵BD∥x轴,
∴点D的纵坐标为3,
∴点D的横坐标为=6,即BD=6,
∴△ABD的面积=×6×3=9;
(3)EF=BD=×6=2,
设E(m,3m+3),
当0<m<2时,点F的坐标为(m+2,3m+3),
∵点F在反比例函数y=上,
∴(m+2)(3m+3)=18,
解得,m1=﹣4(舍去),m2=1,
当m>2时,点F的坐标为(m﹣2,3m+3),
∵点F在反比例函数y=上,
∴(m﹣2)(3m+3)=18,
解得,m3=(舍去),m4=,
综上所述,m的值为1或.
专题19 与二次函数有关的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题19 与二次函数有关的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题19与二次函数有关的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题19与二次函数有关的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共59页, 欢迎下载使用。
专题10 有关面积的最值问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题10 有关面积的最值问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题10有关面积的最值问题的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题10有关面积的最值问题的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
专题09 与线段长度有关的最值问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题09 与线段长度有关的最值问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题09与线段长度有关的最值问题的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题09与线段长度有关的最值问题的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。