专题19 与二次函数有关的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

这是一份专题19 与二次函数有关的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1，文件包含专题19与二次函数有关的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题19与二次函数有关的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。

（1）求抛物线与直线CE的解析式；
（2）求证：PC+PD为定值；
（3）若△PEC的面积为1，求满足条件的点P的坐标．
2．（2021·江苏射阳·九年级月考）如图，在平面直角坐标系中，O是坐标原点，抛物线y＝ax2+bx经过A（﹣4，0），B（﹣3，）两点，连接AB，BO．
（1）求抛物线表达式和直线OB解析式；
（2）点C是第二象限内直线OB上方抛物线上的一个动点，是否存在一点C使△COB面积最大？若存在请求出点C坐标及最大面积，若不存在请说明理由；
（3）若点D从点O出发沿线段OA向点A作匀速运动，速度为每秒1个单位长度，同时线段OA上另一个点H从点A出发沿线段AO向点O作匀速运动，速度为每秒2个单位长度（当点H到达点O时，点D也同时停止运动）．过点D作x轴的垂线，与直线OB交于点E，延长DE到点F，使得EF＝DE，以DF为边，在DF左侧作等边△DGF（当点D运动时点G、点F也随之运动）．过点H作x轴的垂线，与直线AB交于点L，延长HL到点M，使得LM＝HL，以HM为边，在HM的右侧作等边△HMN（当点H运动时，点M、点N也随之运动）．当点D运动t秒时，△DGF有一条边所在直线恰好过△HMN的重心，直接写出此刻t的值．
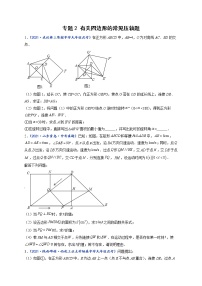
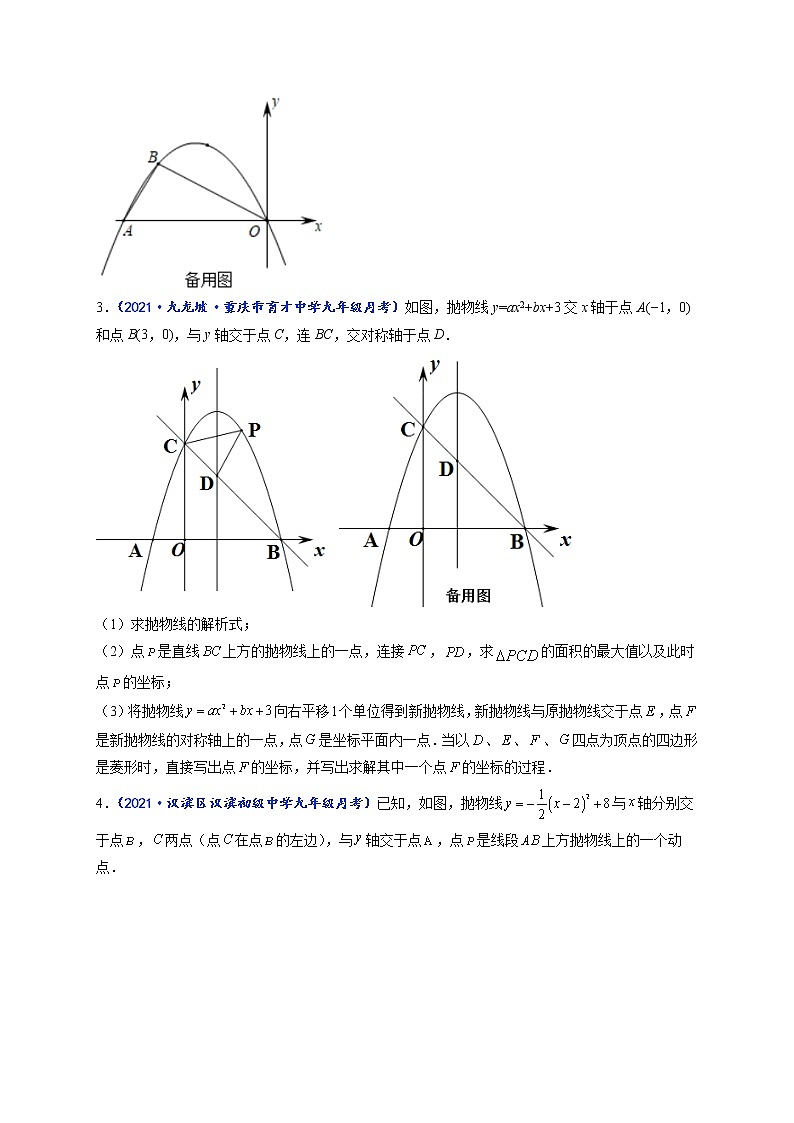
3．（2021·九龙坡·重庆市育才中学九年级月考）如图，抛物线y=ax2+bx+3交x轴于点A(−1，0)和点B(3，0)，与y轴交于点C，连BC，交对称轴于点D．
（1）求抛物线的解析式；
（2）点是直线上方的抛物线上的一点，连接，，求的面积的最大值以及此时点的坐标；
（3）将抛物线向右平移个单位得到新抛物线，新抛物线与原抛物线交于点，点是新抛物线的对称轴上的一点，点是坐标平面内一点．当以、、、四点为顶点的四边形是菱形时，直接写出点的坐标，并写出求解其中一个点的坐标的过程．
4．（2021·汉滨区汉滨初级中学九年级月考）已知，如图，抛物线与轴分别交于点，两点（点在点的左边），与轴交于点，点是线段上方抛物线上的一个动点．
（1）求、、三点坐标；
（2）求直线的解析式；
（3）过点作轴的垂线，交线段于点，再过点做轴交抛物线于点，连结，请问是否存在点使为等腰直角三角形？若存在，求出点的坐标，若不存在，请说明理由．
5．（2021·重庆北碚·西南大学附中九年级月考）如图，已知抛物线与x轴交于点，，与y轴交于点C，且．连接BC，与抛物线的对称轴交于点D．
（1）求抛物线的解析式；
（2）点P是直线上方抛物线上一点，连接、，求面积的最大值，及当面积最大时点P的坐标；
（3）M为抛物线对称轴上一点，N为抛物线上一点，在（2）的基础上，是否存在这样的点M，使得以点P、C、M、N为顶点的四边形为平行四边形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
6．如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，，顶点为D，对称轴交x轴于点E．
（1）求抛物线的解析式、对称轴及顶点D的坐标．
（2）在对称轴上是否存在点N，使得是等腰三角形？若存在，求出点N的坐标；若不存在，请说明理由．
（3）在抛物线上是否存在点P，使得是以AD为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
（4）在抛物线上是否存在一点Q，使得是等边三角形？若存在，求出点Q的坐标；若不存在，请说明理由；
7．（2021·河北·天津外国语大学附属外国语学校九年级月考）如图，抛物线经过点，，．
（1）求抛物线的解析式；
（2）若点为抛物线对称轴上一点，求周长取得最小值时点的坐标；
（3）设抛物线的顶点为，轴于点，在轴上是否存在点使得是直角三角形？若存在，请求出点的坐标；若不存在，请说明理由．
8．（2021·湖北硚口·九年级月考）抛物线C：y＝ax2＋bx－3与x轴交于A(－1，0)，B(3，0)两点，与y轴交于点C．
（1）求抛物线的解析式；
（2）如图1，点D在第四象限的抛物线C上，将绒段DB绕点D逆时针旋转90°，得到线段DE，当点E恰好落在y轴上时，求点D的坐标；
（3）如图2，已知点P(0，－2)，将抛物线C向左平移1个单位长度﹐向上平移4个单位长度，得到抛物线C1．直线y＝kx＋2（k＞0）交抛物线C1于M，N两点（M在N的左边），直线NP交抛物线C1于另－点Q，求证：点M与点Q关于y轴对称．
9．（2021·武汉外国语学校（武汉实验外国语学校）九年级月考）已知，如图，抛物线y＝x2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y＝x﹣2经过A、C两点．
（1）直接写出抛物线的解析式；
（2）P为抛物线上一点，若点P关于直线AC的对称点Q落在y轴上，求P点坐标；
（3）现将抛物线平移，保持顶点在直线y＝x﹣，若平移后的抛物线与直线y＝x﹣2交于M、N两点．①求证：MN的长度为定值；
②结合（2）的条件，直接写出△QMN的周长的最小值
10．（2021·重庆实验外国语学校九年级月考）如图，在平面直角坐标系中，抛物线y＝ax2+bx+3交x轴于A（，0），B（3，0）两点，与y轴交于点C，连接BC，点P是第一象限内抛物线上的一个动点，过点P作PM⊥BC，垂足为点M．
（1）求抛物线的函数表达式；
（2）当PM最大时，求点P的坐标和PM的最大值；
（3）在（2）的条件下，将抛物线y＝ax2+bx+3沿着射线OP的方向平移，使得新抛物线y′过原点，点E为原抛物线y与新抛物线y′的交点，若点G为原抛物线的对称轴上一动点，点H为新抛物线y′上一动点，直接写出所有使得以点A，E，G，H为顶点的四边形是平行四边形的点H的坐标，并把求其中一个点H的坐标的过程写出来．
11．（2021·哈尔滨工业大学附属中学校九年级月考）如图1，抛物线交x轴于点A和点B（点A在点B的左侧），与y轴交于点C，经过点A的直线y＝kx﹣1与抛物线交于点D（4，﹣3）．
（1）求抛物线解析式；
（2）如图2，P为第一象限抛物线上一点，连接PA，PB，设点P的横坐标为t，△PAB的面积为S，请求出S与t的函数关系式（不要求写出自变量的取值范围）；
（3）如图3，在（2）的条件下，当△PAB的面积为时，在AP上方取一点E，连接EA，ED，EP，若∠AED＝45°，∠APE＝2∠PAE，求线段PE的长．

12．（2021·武汉第三寄宿中学九年级月考）如图1，二次函数的图像过点A（-1，3），顶点B的横坐标为1．
（1）求二次函数的解析式;
（2）点P为二次函数第一象限图象上一点，点Q在轴上，若以A、B、P、Q为顶点的四边形是平行四边形，求点P的坐标；
（3）如图3，一次函数（k>0）的图象与该二次函数的图像交于O、C两点，点T为该二次函数图像上位于直线OC下方的动点，过点T作直线交线段OC于点M（不与O、C重合），过点T作直线TN//y轴交OC于点N，若在点T运动的过程中，=常数m，求m、k的值．
13．（2021·长沙市湘郡培粹实验中学九年级月考）定义；若关于x的一元二次方程ax2+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若函数G1的图象与函数G2的图象相交于A、B两点，其中一个点的横坐标等于另一点的横坐标的2倍，则称函数G1与函数G2互为“倍根函数”，A、B两点间的水平距离为“倍宽”．
（1）若是“倍根方程”，求的值；
（2）函数与互为“倍根函数”且“倍宽”为2，求的值；
（3）直线l：y＝tx+d与抛物线L：y＝2x2+px+q（q≠d）互为“倍根函数”，若直线l与抛物线L相交于A（x1，y1），B（x2，y2）两点，且2+2t2≤AB2≤3+3t2，令6x0＝|p﹣t|，若二次函数y0＝﹣（x0﹣m）2+m2+1有最大值4，求实数m的值．
14．（2021·吉林省第二实验学校九年级月考）函数（m为常数）的顶点为点P，设其图象为G．
（1）若点在图象G上，求m的值．
（2）设直线与图象G交于A、B两点，当时，求m的值．
（3）当时，该函数的最大值为5，求m的值．
（4）若图象G在直线和直线间的部分的满足y随x的增大而增大时，且点在直线和直线以及图象G、x轴围城的封闭区域内，直接写出m的取值范围．
15．（2021·福建省泉州实验中学九年级期中）已知抛物线与轴交于和两点，且，与轴交于，且对于该二次函数图象上的任意两点，，当时，总有．
（1）求抛物线的解析式；
（2）过点的直线与该抛物线交于另一点，与线段交于点．
①若，求点的坐标；
②当时，的最小值是，求的值．