初中数学浙教版八年级下册第五章 特殊平行四边形5.3 正方形教课ppt课件

这是一份初中数学浙教版八年级下册第五章 特殊平行四边形5.3 正方形教课ppt课件，共15页。PPT课件主要包含了新知导入，提炼概念，谈一谈，正方形具有什么性质，归纳概念，典例精讲，新知讲解，课堂练习，课堂总结，有一个角是直角等内容，欢迎下载使用。
矩形的性质：性质1：矩形的四个角都是直角. 性质2：矩形的对角线相等.
菱形的性质：性质1：菱形的四条边都相等.性质2 ：菱形的对角线互相垂直,并且每条对角线平分一组对角.
矩形和菱形都具有平行四边形的所有的性质；他们都是轴对称图形,又是中心对称图形.
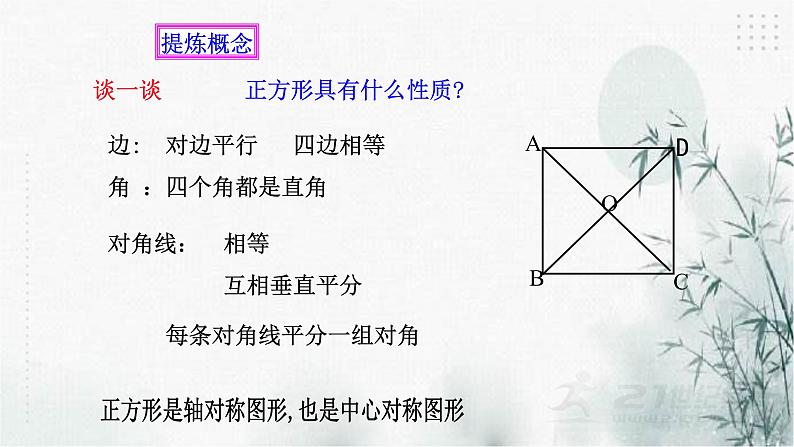
边: 对边平行 四边相等角 ：四个角都是直角
对角线： 相等 互相垂直平分 每条对角线平分一组对角
正方形是轴对称图形,也是中心对称图形
1．正方形的性质定理1：正方形的四个角都是________，四条边________．定理2：正方形的对角线________，并且互相垂直平分，每条对角线平分一组______角．2．正方形的对称性对称性：正方形既是__________图形又是___________图形．它共有4条对称轴，它的对称中心是________的交点．
1.直角 相等 相等 对2.轴对称 中心对称 对角线
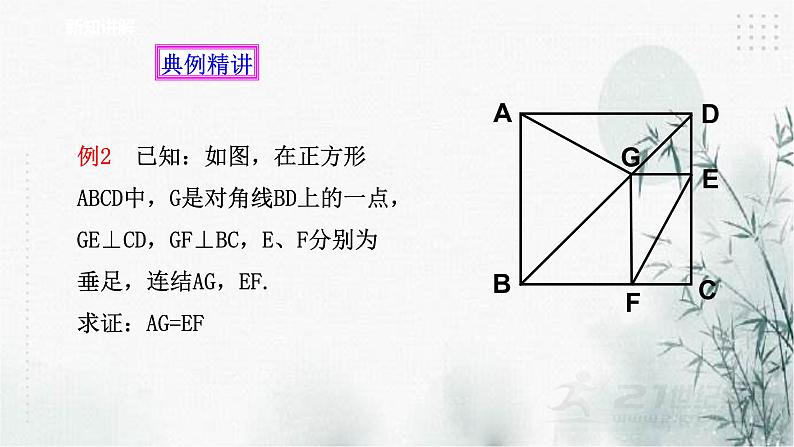
例2 已知：如图，在正方形ABCD中，G是对角线BD上的一点，GE⊥CD，GF⊥BC，E、F分别为垂足，连结AG，EF.求证：AG=EF
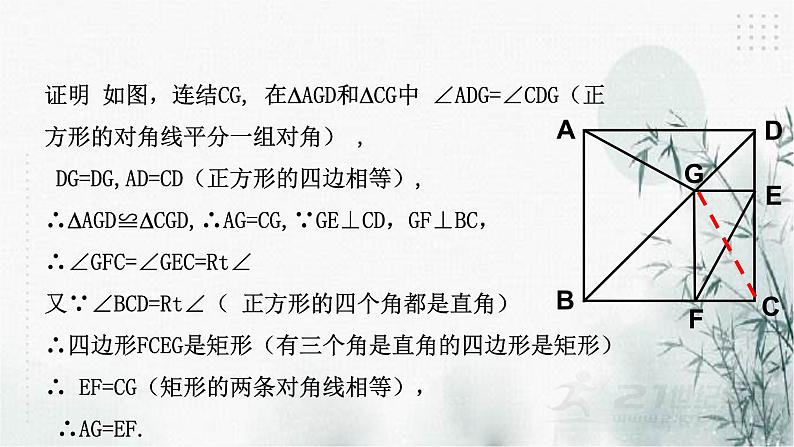
证明 如图，连结CG, 在∆AGD和∆CG中 ∠ADG=∠CDG（正方形的对角线平分一组对角） , DG=DG,AD=CD（正方形的四边相等）,∴∆AGD≌∆CGD,∴AG=CG,∵GE⊥CD，GF⊥BC，∴∠GFC=∠GEC=Rt∠ 又∵∠BCD=Rt∠（ 正方形的四个角都是直角）∴四边形FCEG是矩形（有三个角是直角的四边形是矩形）∴ EF=CG（矩形的两条对角线相等）， ∴AG=EF.
1.正方形具有而菱形不一定具有的性质（ ） A、四条边相等. B、对角线互相垂直平分. C、对角线平分一组对角. D、对角线相等.
2.正方形ABCD中，E是BC延长线上一点，且CE＝AC，AE交DC于点F.试求∠E，∠AFC的度数．
【点悟】正方形四个内角都是直角，四条边都相等，对角线互相垂直平分且相等，每条对角线与边的夹角为45°，正方形是轴对称图形，有4条对称轴．
3.在正方形ABCD中，AC为对角线，E为AC上一点，连结EB，ED.(1)求证：△BEC≌△DEC；(2)延长BE交AD于F，当∠BED＝120°时，求∠EFD的度数．
解：(1)证明：∵四边形ABCD是正方形，∴BC＝CD，∠ECB＝∠ECD＝45°.又∵EC＝EC，∴△BEC≌△DEC；(2)∵△BEC≌△DEC，∴∠BEC＝∠DEC＝1/2∠BED.∵∠BED＝120°，∴∠BEC＝60°＝∠AEF，∴∠EFD＝60°＋45°＝105°.
4.如图，在正方形ABCD中，G是BC上任意一点，连结AG，DE⊥AG于E，BF∥DE交AG于F，探究线段AF，BF，EF三者之间的数量关系，并说明理由．
解：AF＝BF＋EF.理由如下：如答图，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝90°，∴∠1＋∠2＝90°，∵DE⊥AG，∴∠AED＝90°，∠2＋∠3＝90°，∴∠1＝∠3，∵BF∥DE，∴∠BFA＝∠AED，∴△ABF≌△DAE(AAS)，∴AE＝BF，∵AF＝AE＋EF，∴AF＝BF＋EF.
1．正方形的性质定理1：正方形的四个角都是________，四条边________．定理2：正方形的对角线________，并且互相垂直平分，每条对角线平分一组______角．直角 相等 相等 对2．正方形的对称性对称性：正方形既是__________图形又是___________图形．它共有4条对称轴，它的对称中心是________的交点．轴对称 中心对称 对角线3.正方形的四个内角都是直角，四条边都相等，对角线互相垂直平分且相等，每条对角线与边的夹角为45°，正方形是轴对称图形，有4条对称轴．