人教版 (五四制)七年级下册第18章 全等三角形综合与测试单元测试课后测评

这是一份人教版 (五四制)七年级下册第18章 全等三角形综合与测试单元测试课后测评，共15页。试卷主要包含了下列各组图形中，是全等形的是，能使两个直角三角形全等的条件是，全等图形是指两个图形等内容，欢迎下载使用。
2021-2022学年人教五四新版七年级下册数学《第18章 全等三角形》单元测试卷
一．选择题（共11小题，满分33分）
1．如图，在下列4个正方形图案中，与左边正方形图案全等的图案是（　　）

A． B． C． D．
2．下列各组图形中，是全等形的是（　　）
A．两个含60°角的直角三角形
B．腰对应相等的两个等腰直角三角形
C．边长为3和4的两个等腰三角形
D．一个钝角相等的两个等腰三角形
3．能使两个直角三角形全等的条件是（　　）
A．斜边相等 B．两直角边对应相等
C．两锐角对应相等 D．一锐角对应相等
4．如图，将两根钢条AA′、BB′的中点O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（　　）

A．SAS B．ASA C．SSS D．AAS
5．全等图形是指两个图形（　　）
A．大小相同 B．形状相同
C．能够完全重合 D．相等
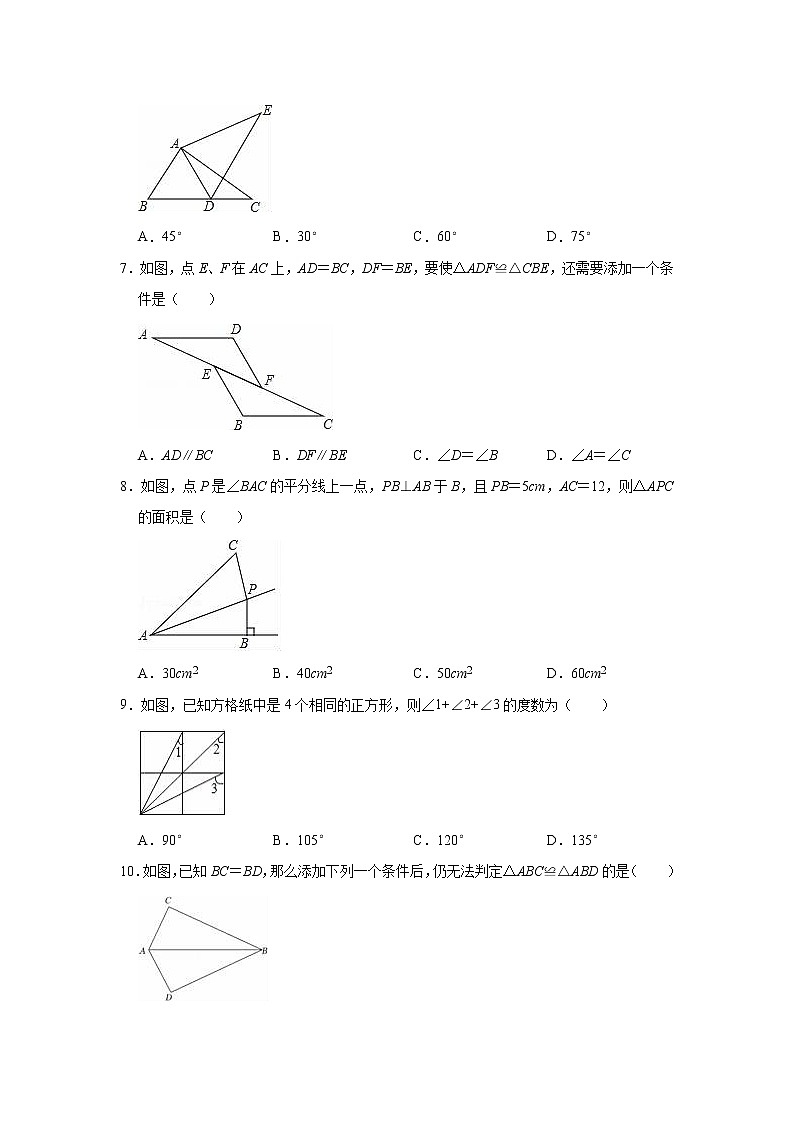
6．如图，△ABC≌△ADE，点D落在BC上，且∠B＝60°，则∠EDC的度数等于（　　）

A．45° B．30° C．60° D．75°
7．如图，点E、F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加一个条件是（　　）

A．AD∥BC B．DF∥BE C．∠D＝∠B D．∠A＝∠C
8．如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB＝5cm，AC＝12，则△APC的面积是（　　）

A．30cm2 B．40cm2 C．50cm2 D．60cm2
9．如图，已知方格纸中是4个相同的正方形，则∠1+∠2+∠3的度数为（　　）

A．90° B．105° C．120° D．135°
10．如图，已知BC＝BD，那么添加下列一个条件后，仍无法判定△ABC≌△ABD的是（　　）

A．AC＝AD B．∠ABC＝∠ABD C．∠C＝∠D＝90° D．∠CAB＝∠DAB
11．如图，在△ABC中，BD平分∠ABC，∠C＝2∠CDB，AB＝12，CD＝3，则△ABC的周长为（　　）

A．21 B．24 C．27 D．30
二．填空题（共10小题，满分30分）
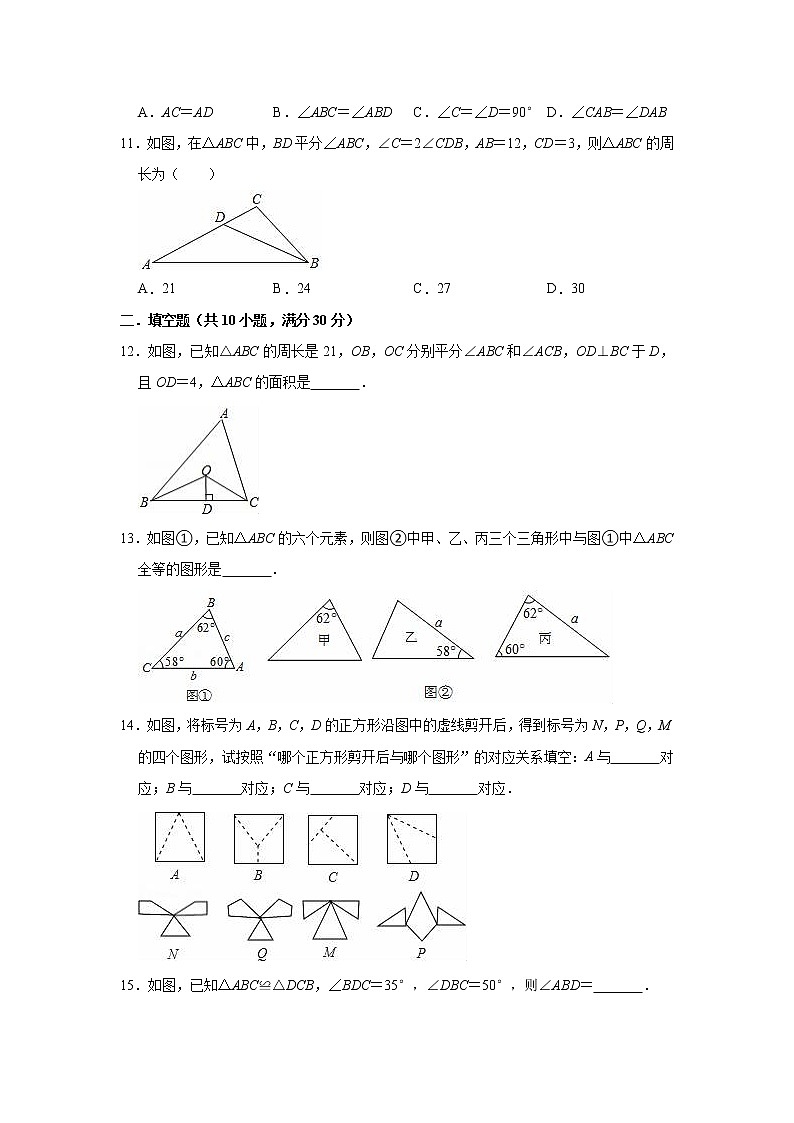
12．如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝4，△ABC的面积是　 　．

13．如图①，已知△ABC的六个元素，则图②中甲、乙、丙三个三角形中与图①中△ABC全等的图形是　 　．

14．如图，将标号为A，B，C，D的正方形沿图中的虚线剪开后，得到标号为N，P，Q，M的四个图形，试按照“哪个正方形剪开后与哪个图形”的对应关系填空：A与　 　对应；B与　 　对应；C与　 　对应；D与　 　对应．

15．如图，已知△ABC≌△DCB，∠BDC＝35°，∠DBC＝50°，则∠ABD＝　 　．

16．如图，已知∠1＝∠2，要判定△ABD≌△ACD，请你添加一个条件，是　 　．（写出一个条件即可）

17．如图，在△ABC和△DEF中，∠A＝∠D＝90°，AC＝DE，若要用“斜边直角边（H．L．）”直接证明Rt△ABC≌Rt△DEF，则还需补充条件：　 　．

18．如图，在由6个相同的小正方形拼成的网格中，∠2﹣∠1＝　 　°．

19．如图，∠A＝∠B＝90°，AB＝100，E，F分别为线段AB和射线BD上的一点，若点E从点B出发向点A运动，同时点F从点B出发向点D运动，二者速度之比为2：3，运动到某时刻同时停止，在射线AC上取一点G，使△AEG与△BEF全等，则AG的长为 　 　．

20．如图，课间小明拿着老师的等腰三角板玩，不小心掉到两条凳子之间（凳子与地面垂直）．已知DC＝3，CE＝4．则两条凳子的高度之和为 　 　．

21．如图，在△ACD中，∠CAD＝90°，AC＝6，AD＝8，AB∥CD，E是CD上一点，BE交AD于点F，若EF＝BF，则图中阴影部分的面积为　 　．

三．解答题（共6小题，满分57分）
22．已知，如图，△ABC≌△DEF，求证：AC∥DF．

23．如图，AB＝AC，请你添加一个条件，使△ABE≌△ACD，
（1）你添加的条件是　 　；
（2）根据上述添加的条件证明△ABE≌△ACD．

24．如图所示，CD＝CA，∠1＝∠2，EC＝BC，求证：△ABC≌△DEC．

25．如图所示，△ABC≌△ADE，且∠CAD＝10°，∠D＝25°，∠EAB＝120°，求∠DFB的度数．

26．我们知道能完全重合的图形叫做全等图形，因此，如果两个四边形能完全重合，那么这两个四边形全等，也就是说，当两个四边形的四个内角、四条边都分别对应相等时，这两个四边形全等．请借助三角形全等的知识，解决有关四边形全等的问题．
如图，已知，四边形ABCD和四边形A′B′C′D′中，AB＝A′B′，BC＝B′C′，∠B＝∠B′，∠C＝∠C′，现在只需补充一个条件，就可得四边形ABCD≌四边形A′B′C′D′．
下列四个条件：①∠A＝∠A′；②∠D＝∠D′；③AD＝A′D′；④CD＝C′D′
（1）其中，符合要求的条件是　 　．（直接写出编号）
（2）选择（1）中的一个条件，证明四边形ABCD≌四边形A′B′C′D′．

27．如图，已知在△ABC中，AB＝AC，∠BAC＝90°，分别过B、C向过A的直线作垂线，垂足分别为E、F．
（1）如图①过A的直线与斜边BC不相交时，求证：EF＝BE+CF；
（2）如图②过A的直线与斜边BC相交时，其他条件不变，若BE＝10，CF＝3，求：FE长．


参考答案与试题解析
一．选择题（共11小题，满分33分）
1．解：能够完全重合的两个图形叫做全等形．
A、B、D图案均与题干中的图形不重合，所以不属于全等的图案，
C中的图案旋转180°后与题干中的图形重合．
故选：C．
2．解：A、两个含60°角的直角三角形，缺少对应边相等，所以不是全等形；
B、腰对应相等的两个等腰直角三角形，符合AAS或ASA，或SAS，是全等形；
C、边长为3和4的两个等腰三角形有可能是3，3，4或4，4，3不一定全等对应关系不明确不一定全等；
D、一个钝角相等的两个等腰三角形．缺少对应边相等，不是全等形．
故选：B．
3．解：A选项，无法证明两条直角边对应相等，因此A错误．
C、D选项，在全等三角形的判定过程中，必须有边的参与，因此C、D选项错误．
B选项的根据是全等三角形判定中的SAS判定．
故选：B．
4．解：∵O是AA′、BB′的中点，
∴AO＝A′O，BO＝B′O，
在△OAB和△OA′B′中，
∴△OAB≌△OA′B′（SAS），
故选：A．
5．解：全等图形是指两个图形的形状和大小都相等，
故选：C．
6．解：∵△ABC≌△ADE，
∴∠B＝∠ADE＝60°，AB＝AD，
∴∠ADB＝∠B＝60°，
∴∠EDC＝60°．
故选：C．
7．解：∠D＝∠B，
理由是：∵在△ADF和△CBE中

∴△ADF≌△CBE（SAS），
即选项C正确；
具备选项A、选项B，选项D的条件都不能推出两三角形全等，
故选：C．
8．解：过P作PD⊥AC于D，
∵点P是∠BAC的平分线上一点，PB⊥AB于B，
∴PD＝PB＝5cm，
∴S△APC＝AC•PD＝12×5＝30cm2，
故选：A．

9．解：观察图形可知，∠1所在的三角形与∠3所在的三角形全等，
∴∠1+∠3＝90°，
又∠2＝45°，
∴∠1+∠2+∠3＝135°，
故选：D．
10．解：A、添加AC＝AD，根据SSS，能判定△ABC≌△ABD，故A选项不符合题意；
B、添加∠ABC＝∠ABD，根据SAS，能判定△ABC≌△ABD，故B选项不符合题意；
C、添加∠C＝∠D＝90°时，根据HL，能判定△ABC≌△ABD，故C选项不符合题意；
D、添加∠CAB＝∠DAB，SSA不能判定△ABC≌△ABD，故D选项符合题意；
故选：D．
11．解：如图，在AB上截取BE＝BC，连接DE，

∵BD平分∠ABC，
∴∠ABD＝∠CBD，
在△CBD和△EBD中，
，
∴△CBD≌△EBD（SAS），
∴∠CDB＝∠BDE，∠C＝∠DEB，
∵∠C＝2∠CDB，
∴∠CDE＝∠DEB，
∴∠ADE＝∠AED，
∴AD＝AE，
∴△ABC的周长＝AD+AE+BE+BC+CD＝AB+AB+CD＝27，
故选：C．
二．填空题（共10小题，满分30分）
12．解：
过O作OE⊥AB于E，OF⊥AC于F，连接OA，
∵OB，OC分别平分∠ABC和∠ACB，OD⊥BC，
∴OE＝OD，OD＝OF，
即OE＝OF＝OD＝4，
∴△ABC的面积是：S△AOB+S△AOC+S△OBC
＝×AB×OE+×AC×OF+×BC×OD
＝×4×（AB+AC+BC）
＝×4×21＝42，
故答案为：42．
13．解：已知图①的△ABC中，∠B＝62°，BC＝a，AB＝c，AC＝b，∠C＝58°，∠A＝60°，
图②中，甲：只有一个角和∠B相等，没有其它条件，不符合三角形全等的判定定理，即和△ABC不全等；
乙：只有一个角和∠B相等，还有一条边，没有其它条件，不符合三角形全等的判定定理，即和△ABC不全等；
丙：符合AAS定理，能推出两三角形全等；
故答案为：丙．
14．解：由全等形的概念可知：
A是三个三角形，与M对应；
B是一个三角形和两个直角梯形，与N对应；
C是一个三角形和两个四边形，与Q对应；
D是两个三角形和一个四边形，与P对应
故分别填入M，N，Q，P．
15．解：∵∠BDC＝35°，∠DBC＝50°，
∴∠BCD＝180°﹣∠BDC﹣∠DBC＝180°﹣35°﹣50°＝95°，
∵△ABC≌△DCB，
∴∠ABC＝∠BCD＝95°，
∴∠ABD＝∠ABC﹣∠DBC＝95°﹣50°＝45°．
故答案为：45°．
16．解：判断△ABD≌△ACD，已知的条件是：∠1＝∠2，AD＝AD，
因而根据SAS，可以添加条件：AB＝AC；
根据AAS，可以添加条件：∠B＝∠C；
根据ASA可以添加∠ADB＝∠ADC．
故答案是：AB＝AC或∠B＝∠C或∠ADB＝∠ADC．
17．解：在Rt△ABC和Rt△DEF中，
，
∴Rt△ABC≌Rt△DEF（HL），
故答案为：BC＝EF
18．解：如图所示：

由图可知△ABF与△CED全等，
∴∠BAF＝∠ECD，
∴∠2﹣∠1＝90°，
故答案为：90．
19．解：设BE＝2t，则BF＝3t，因为∠A＝∠B＝90°，使△AEG与△BEF全等，可分两种情况：
情况一：当BE＝AG，BF＝AE时，
∵BF＝AE，AB＝100，
∴3t＝100﹣2t，
解得：t＝20，
∴AG＝BE＝2t＝2×20＝40；
情况二：当BE＝AE，BF＝AG时，
∵BE＝AE，AB＝100，
∴2t＝100﹣2t，
解得：t＝25，
∴AG＝BF＝3t＝3×25＝75，
综上所述，AG＝40或AG＝75．
故答案为：40或75．
20．解：由题意可得：∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，
则∠DAC＝∠BCE，
在△ACD和△CBE中，
，
∴△ACD≌△CBE（AAS），
故DC＝BE＝3，AD＝CE＝4，
则两条凳子的高度之和为：3+4＝7．
故答案为：7．
21．解：∵AB∥CD，
∴∠BAD＝∠D，
在△BAF和△EDF中，
，
∴△BAF≌△EDF（ASA），
∴S△BAF＝S△DEF，
∴图中阴影部分的面积＝S四边形ACEF+S△AFB＝S△ACD＝＝＝24．
故答案为：24．
三．解答题（共6小题，满分57分）
22．证明：∵△ABC≌△DEF，
∴∠ACB＝∠DFE，
∴AC∥DF．
23．解：（1）添加的条件是∠B＝∠C或AE＝AD．
故答案为：AD＝AE或∠B＝∠C（答案不唯一）；
　
（2）若添加∠B＝∠C，
在△ABE和△ACD中
∵，
∴△ACD≌△ABE（ASA）．
24．证明：∵∠1＝∠2，
∴∠ACB＝∠DCE，
在△ABC和△DEC中，
，
∴△ABC≌△DEC（SAS）．
25．解：∵△ABC≌△ADE，∠D＝25°，
∴∠B＝∠D＝25°，∠EAD＝∠CAB．
∵∠EAB＝∠EAD+∠CAD+∠CAB＝120°，∠CAD＝10°，
∴∠CAB＝（120°﹣10°）÷2＝55°，
∴∠FAB＝∠CAB+∠CAD＝55°+10°＝65°．
又∵∠DFB是△ABF的外角，
∴∠DFB＝∠B+∠FAB，
∴∠DFB＝25°+65°＝90°．
26．解：（1）符合要求的条件是①②④，
故答案为：①②④；
（2）选④，
证明：连接AC、A′C′，
在△ABC与△A′B′C′中，，
∴△ABC≌△A′B′C′（SAS），
∴AC＝A′C′，∠ACB＝∠A′C′B′，
∵∠BCD＝∠B′C′D′，
∴∠BCD﹣∠ACB＝∠B′C′D′﹣∠A′C′B′，
∴∠ACD＝∠A′C′D′，
在△ACD和△A′C′D中，
，
∴△ACD≌△A′C′D′（SAS），
∴∠D＝∠D，∠DAC＝∠D′A′C′，DA＝D′A′，
∴∠BAC+∠DAC＝∠B′A′C′+∠D′A′C′，
即∠BAD＝∠B′A′D′，
∴四边形ABCD和四边形A′B′C′D′中，
AB＝A′B′，BC＝B′C′，AD＝A′D′，DC＝D′C′，
∠B＝∠B′，∠BCD＝∠B′C′D′，∠D＝∠D′，∠BAD＝∠B′A′D′，
∴四边形ABCD≌四边形A′B′C′D′．

27．（1）证明：∵BE⊥EA，CF⊥AF，
∴∠BAC＝∠BEA＝∠CFE＝90°，
∴∠EAB+∠CAF＝90°，∠EBA+∠EAB＝90°，
∴∠CAF＝∠EBA，
在△ABE和△AFC中，
∠BEA＝∠AFC＝90°，∠EBA＝∠CAF，AB＝AC，
∴△BEA≌△AFC（AAS）．
∴EA＝FC，BE＝AF．
∴EF＝EB+CF．

（2）解：∵BE⊥EA，CF⊥AF，
∴∠BAC＝∠BEA＝∠CFE＝90°，
∴∠EAB+∠CAF＝90°，∠ABE+∠EAB＝90°，
∴∠CAF＝∠ABE，
在△ABE和△AFC中，
∠BEA＝∠AFC＝90°，∠EBA＝∠CAF，AB＝AC，
∴△BEA≌△AFC（AAS）．
∴EA＝FC＝3，BE＝AF＝10．
∴EF＝AF﹣CF＝10﹣3＝7．