




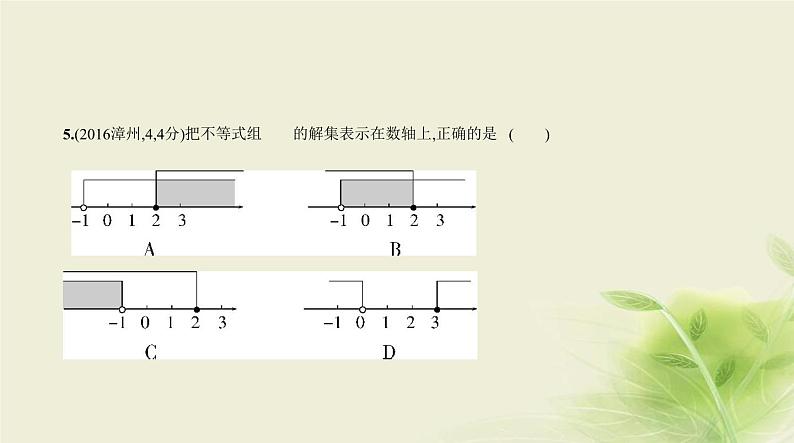

























中考数学总复习 02第二章 方程(组)与不等式(组) PPT课件(福建专用)
展开2016—2020年全国中考题组
1.(2020重庆A卷,7,4分)解一元一次方程 (x+1)=1- x时,去分母正确的是 ( )A.3(x+1)=1-2x B.2(x+1)=1-3xC.2(x+1)=6-3x D.3(x+1)=6-2x
答案 D 去分母是方程两边同乘最简公分母6,所以D正确,故选D.
易错警示 方程两边同乘一个不为0的数时,每一项都应该乘这个数.
2.(2019福建,8,4分)《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问君每 日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问 他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的 是 ( )A.x+2x+4x=34 685 B.x+2x+3x=34 685C.x+2x+2x=34 685 D.x+ x+ x=34 685
答案 A 由题意知第二天读2x个字,第三天读4x个字,则x+2x+4x=34 685.故选A.
解题关键 本题考查了一元一次方程的应用.解题的关键是找出等量关系,并能用含未知数的代数式表 示出第二天,第三天的读字量.
3.(2016南平,9,4分)闽北某村原有林地120公顷,旱地60公顷,为适应产业结构调整,需把一部分旱地改造 为林地,改造后,旱地面积占林地面积的20%,设把x公顷旱地改造为林地,则可列方程为 ( )A.60-x=20%(120+x) B.60+x=20%×120C.120-x=20%(60+x) D.60-x=20%×120
答案 A 根据题意可得60-x=20%(120+x).
4.(2016福州,22,8分)某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元, 甲乙两种票各买了多少张?
解析 设甲种票买了x张,则乙种票买了(35-x)张.由题意,得24x+18(35-x)=750,解得x=20.∴35-x=15.答:甲种票买了20张,乙种票买了15张.
5.(2017湖北武汉,17,8分)解方程4x-3=2(x-1).
方法规律 解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.
6.(2020福建,20,8分)某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙 特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和 都是100吨,且甲特产的销售量都不超过20吨.(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各 多少吨?(2)求该公司一个月销售这两种特产所能获得的最大总利润.
解析 本题考查一元一次方程、一次函数的性质等基础知识,考查运算能力、应用意识,考查函数与方 程思想.(1)设这个月该公司销售甲特产x吨,则销售乙特产(100-x)吨.依题意,得10x+(100-x)=235,解得x=15,则100-x=85.经检验x=15符合题意.所以,这个月该公司销售甲特产15吨,乙特产85吨.(2)设一个月销售甲特产m吨,公司获得的总利润为w万元,则销售乙特产(100-m)吨,且0≤m≤20.w=(10.5-10)m+(1.2-1)(100-m)=0.3m+20.因为0.3>0,所以w随着m的增大而增大.又因为0≤m≤20,所以当m=20时,公司获得的总利润最大,为26万元.故该公司一个月销售这两种特产能获得的最大总利润为26万元.
7.(2019重庆A卷,24,10分)某文明小区有50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平 方米住宅套数的2倍.物管公司每月月底按每平方米2元收取当月物管费,该小区全部住宅都入住且每户 均按时全额缴纳物管费.(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80 平方米的住户分别有40%和20%参加了此次活动.为提高大家的积极性,6月份准备把活动一升级为活动 二:“垃圾分类抵扣物管费”,同时终止活动一.经调查与测算,参加活动一的住户会全部参加活动二,参 加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数 的基础上将增加2a%,每户物管费将会减少 a%;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加6a%,每户物管费将会减少 a%.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少 a%,求a的值.
解题关键 本题数据较多,分清楚题目中的数量关系,根据等量关系列出方程是解题的关键.
考点二 一元二次方程
1.(2016厦门,2,4分)方程x2-2x=0的根是 ( )A.x1=x2=0 B.x1=x2=2C.x1=0,x2=2 D.x1=0,x2=-2
答案 C 易知x(x-2)=0,∴x=0或x-2=0,∴x1=0,x2=2.故选C.
2.(2016莆田,7,4分)关于x的一元二次方程x2+ax-1=0的根的情况是 ( )A.没有实数根B.只有一个实数根C.有两个相等的实数根D.有两个不相等的实数根
答案 D ∵Δ=a2-4×1×(-1)=a2+4≥4,∴方程有两个不相等的实数根.
3.(2020广东广州,9,3分)直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是 ( )A.0个 B.1个C.2个 D.1个或2个
答案 D ∵直线y=x+a不经过第二象限,∴a≤0.当a=0时,方程为2x+1=0,只有一个实数解;当a<0时,方程ax2+2x+1=0为一元二次方程,Δ=4-4a>0,∴方程有两个解.故方程有1个解或2个解.故选D.
易错警示 本题易将a=0的情况漏掉,从而错选C.
4.(2020辽宁营口,8,3分)一元二次方程x2-5x+6=0的解为 ( )A.x1=2,x2=-3 B.x1=-2,x2=3C.x1=-2,x2=-3 D.x1=2,x2=3
一题多解 本题也可以使用十字相乘法.原方程可化为(x-2)(x-3)=0,所以x1=2,x2=3.
5.(2016福州,12,3分)下列选项中,能使关于x的一元二次方程ax2-4x+c=0一定有实数根的是 ( )A.a>0 B.a=0C.c>0 D.c=0
答案 D 若一元二次方程ax2-4x+c=0有实数根,则Δ=(-4)2-4ac=16-4ac≥0,且a≠0.∴ac≤4,且a≠0.A.若a>0,则当a=1,c=5时,ac=5>4,故此选项不符合题意;B.a=0不符合一元二次方程的定义,故此选项不符合题意;C.若c>0,则当a=1,c=5时,ac=5>4,故此选项不符合题意;D.若c=0,则ac=0≤4,故此选项符合题意.故选D.
易错警示 方程的根的情况应根据根的判别式进行判断,不能盲目求解.
6.(2019河北,15,2分)小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c比原方程的c值小2,则原方程的根的情况是( )A.不存在实数根B.有两个不相等的实数根C.有一个根是x=-1D.有两个相等的实数根
答案 A 只抄对了a=1,b=4,即x2+4x+c=0,把x=-1代入得c=3,因为所抄的c比原方程的c值小2,所以c值应 该为5,原方程为x2+4x+5=0,Δ=42-4×1×5=-4<0,所以原方程不存在实数根,故选A.
7.(2018福建,10,4分)已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确 的是 ( )A.1一定不是关于x的方程x2+bx+a=0的根B.0一定不是关于x的方程x2+bx+a=0的根C.1和-1都是关于x的方程x2+bx+a=0的根D.1和-1不都是关于x的方程x2+bx+a=0的根
答案 D 由Δ=(2b)2-4(a+1)2=0得b=±(a+1),因为a+1≠0,所以b≠0.①当b=-(a+1)时,x=1是方程x2+bx+a=0的根;②a+1≠0,a可以取0,故x=0可能是方程x2+bx+a=0的根;③当b=a+1时,x=-1是方程x2+bx+a=0的根.因为b=-(a+1)和b=a+1不能同时成立,所以x=1和x=-1不能同时为方程x2+bx+a=0的根,故选D.
8.(2019山西,13,3分)如图,在一块长12 m,宽8 m的矩形空地上,修建同样宽的两条互相垂直的道路(两条 道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77 m2.设道路的宽为x m,则根据 题意,可列方程为 .
答案 (12-x)(8-x)=77(或x2-20x+19=0)
解析 由题意得(12-x)(8-x)=77,变形可得x2-20x+19=0.
思路分析 把两条道路分别平移到矩形的最上边和最左边,则剩下的部分为一个长方形,根据长方形的 面积公式列出方程.
9.(2019北京,19,5分)关于x的方程x2-2x+2m-1=0有实数根,且m为正整数,求m的值及此时方程的根.
解析 由题意,得Δ=(-2)2-4(2m-1)≥0.解得m≤1.∵m为正整数,∴m=1.此时,方程为x2-2x+1=0.解得x1=x2=1.∴m=1,方程的根为x1=x2=1.
10.(2018内蒙古呼和浩特,23,7分)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,请你用 配方法探索有实数根的条件,并推导出求根公式,证明x1·x2= .
解题关键 正确解决本题的关键是要通过求根公式进行验证,同时要具有计算含字母系数的方程的能 力.
1.(2016广西南宁,10,3分)超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个 又减10元,经两次降价后售价为90元,则可列方程为 ( ) D.x-0.8x-10=90
答案 A 每个书包原价是x元,则第一次打八折后的价格是0.8x元,第二次降价10元后的价格是(0.8x-10)元,故可列方程为0.8x-10=90.故选A.
2.(2018内蒙古呼和浩特,13,3分)文具店销售某种笔袋,每个18元,小华去购买这种笔袋,结账时店员说: “如果你再多买一个就可以打九折,价钱比现在便宜36元.”小华说:“那就多买一个吧,谢谢.”根据两 人的对话可知,小华结账时实际付款 元.
解析 设小华计划买x个笔袋,则可列方程为18x-18×0.9×(x+1)=36,解得x=29.故小华结账时实际付款18× 0.9×30=486(元).
3.(2020吉林,10,3分)我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天 走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,根据 题意,可列方程为 .
答案 (240-150)x=150×12
解析 根据“跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马x天追上慢马”,可 列方程为(240-150)x=150×12.
方法总结 列方程(组)解应用题,关键是把已知量和未知量联系起来,找出题目中的等量关系.一般来说, 有几个未知量,就列几个方程.在列方程时注意:(1)方程两边表示的是同类量;(2)同类量的单位要统一;(3)方程两边的数值要相等.
1.(2020新疆,5,5分)下列一元二次方程中,有两个不相等实数根的是 ( )A.x2-x+ =0 B.x2+2x+4=0C.x2-x+2=0 D.x2-2x=0
2.(2019河南,6,3分)一元二次方程(x+1)(x-1)=2x+3的根的情况是 ( )A.有两个不相等的实数根 B.有两个相等的实数根C.只有一个实数根 D.没有实数根
答案 A 将一元二次方程(x+1)(x-1)=2x+3整理得,x2-2x-4=0,Δ=b2-4ac=20>0,所以此一元二次方程有两 个不相等的实数根,故选A.
3.(2019内蒙古呼和浩特,8,3分)若x1,x2是一元二次方程x2+x-3=0的两个实数根,则 -4 +17的值为( )A.-2 B.6 C.-4 D.4
4.(2018安徽,7,4分)若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为 ( )A.-1 B.1 C.-2或2 D.-3或1
答案 A 原方程可化为x2+(a+1)x=0,由题意得Δ=(a+1)2=0,解得a=-1,故选A.
5.(2019山西,8,3分)一元二次方程x2-4x-1=0配方后可化为 ( )A.(x+2)2=3 B.(x+2)2=5C.(x-2)2=3 D.(x-2)2=5
答案 D x2-4x-1=0,(x2-4x+4)-4-1=0,(x-2)2=5,故选D.
6.(2018新疆乌鲁木齐,9,4分)宾馆有50间房供游客居住.当每间房每天定价为180元时,宾馆会住满;当每 间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出20元 的费用.当房价定为多少元时,宾馆当天的利润为10 890元?设房价定为x元,则有 ( )A.(180+x-20) =10 890B.(x-20) =10 890C.x -50×20=10 890D.(x+180) -50×20=10 890
答案 B 当房价定为x元时,空闲的房间有 间,所以有游客居住的房间有 间,则宾馆当天的利润为 (x-20)元,故B正确.
思路分析 先求出房价定为x元时有游客居住的房间数,而每间房的利润就是房价减去支出的20元,从而 得出宾馆当天的利润,列等式即可.
7.(2017河北,19,4分)对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1.因此,min{- ,- }= ;若min{(x-1)2,x2}=1,则x= .
A组 2018—2020年模拟·基础题组时间:60分钟 分值:80分
一、选择题(每小题4分,共12分)
1.(2020福州福清线上质检,5)如图表示解方程3-5x=2(2-x)的过程,其中依据“等式的性质”的步骤是 ( ) A.①② B.②③ C.③④ D.②④
答案 D ①是去括号,依据“去括号法则”;②是移项,依据“等式的性质1”;③是合并同类项,利用 “合并同类项法则”;④是系数化为1,依据“等式的性质2”.故选D.
解后反思 本题考查解一元一次方程,熟练掌握运算法则是解题关键.
2.(2020泉州二检,8)关于x的一元二次方程ax2+a=0根的情况是 ( )A.有两个实数根 B.有两个相等的实数根C.有两个不等的实数根 D.无实数根
答案 D 由题意知a≠0.∵ax2+a=0,∴Δ=0-4a2<0,故选D.
方法总结 一元二次方程根的判别式Δ=b2-4ac,Δ>0时,方程有两个不相等的实数根,Δ=0时,方程有两个 相等的实数根,Δ<0时,方程没有实数根.
3.(2020漳州一检,1)下列方程属于一元二次方程的是 ( )A.x2=0 B.3(x2-1)=2(y-1)C.ax2-3x+1=0 D. +x+1=0
答案 A B中有两个未知数,故B错.C中a为0时不是一元二次方程,故C错.D中方程不是整式方程,故D 错.故A对.
易错警示 ax2+bx+c=0不一定是一元二次方程.
二、填空题(每小题4分,共16分)
4.(2020漳州二检,13)若a是方程x2+x-1=0的根,则代数式2 020-a2-a的值是 .
解析 2 020-a2-a=2 020-(a2+a).∵a2+a-1=0,∴a2+a=1.∴2 020-a2-a=2 020-1=2 019.
5.(2020南平一检,11)已知x=1是关于x的方程x2-a=0的解,则a= .
解析 将x=1代入x2-a=0,得1-a=0,解得a=1.
6.(2019福州一检,15)我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中 间有个方池.丈量田地待耕犁,恰好三分在记.池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第 一.”其大意为:有一块圆形的田地,中间有一块正方形水池.测量出除水池外圆内可耕地的面积恰好72 平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形的边长和圆的直径,那么你的计算水平就 是第一了.设正方形的边长是x步,则列出的方程是 .
答案 π -x2=72
7.(2020漳州一检,11)一元二次方程x2-2x+m=0配方后得(x-1)2=n,则m+n的值是 .
解析 化简(x-1)2=n得x-2x+1=n,对比一元二次方程x2-2x+m=0可得m=1,n=0.∴m+n=1+0=1.
三、解答题(共42分)
8.(2018泉州质检,17)解方程: - =1.
解析 去分母,得3(x-3)-2(2x+1)=6,去括号,得3x-9-4x-2=6,移项,得3x-4x=6+9+2,合并同类项,得-x=17,系数化为1,得x=-17.
9.(2020福州一检,17)解方程:x2-6x-1=0.
10.(2019泉州二检,20)《杨辉算法》中有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多 几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?
解析 设矩形田地的长为x步,则宽为(60-x)步. (1分)依题意得x(60-x)=864, (5分)整理得x2-60x+864=0,解得x=36或x=24(不符合题意,舍去), (7分)∴60-x=60-36=24,∴36-24=12(步).答:该矩形田地的长比宽多12步. (8分)
11.(2020厦门一检,21)梭梭树因其顽强的生命力和防风固沙的作用,被称为“沙漠植被之王”.新疆北部 某沙漠2016年有16万亩梭梭树,经过两年的人工种植和自然繁殖,2018年达到25万亩.按这两年的年平均 增长率,请估计2019年该沙漠梭梭树的面积.
12.(2020福州福清线上质检,23)在两周内,某水果店标价为10元/斤的某种水果经过两次降价后的价格为 8.1元/斤,并且两次降价的百分率相同.(1)求该水果每次降价的百分率;(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
已知该水果的进价为4.1元/斤,设销售该水果第x天的利润为y元,求y与x(1≤x<15)之间的函数解析式,并 求出第几天的销售利润最大.
解析 (1)设该水果每次降价的百分率是m,依题意得,10(1-m)2=8.1, (3分)解得m=10%或m=190%(不合题意,舍去),答:该水果每次降价的百分率是10%. (5分)(2)当1≤x<9时,第1次降价后的价格为10×(1-10%)=9元, (6分)∴y=(9-4.1)(80-3x)-(40+3x)=-17.7x+352, (7分)∵-17.7<0,∴y随x的增大而减小,∴当x=1时,y有最大值,y最大=-17.7+352=334.3(元),(8分)当9≤x<15时,第2次降价后的价格为8.1元,∴y=(8.1-4.1)(120-x)-(3x2-64x+400)=-3x2+60x+80=-3(x-10)2+380, (9分)∵-3<0,∴当x=10时,y有最大值,y最大=380(元).综上所述,第10天的销售利润最大. (10分)
B组 2018—2020年模拟·提升题组时间:20分钟 分值:32分
一、选择题(每小题4分,共20分)
1.(2019厦门二检,7)若方程(x-m)(x-a)=0(m≠0)的根是x1=x2=m,则下列结论正确的是 ( )A.a=m,且a是该方程的根B.a=0,且a是该方程的根C.a=m,但a不是该方程的根D.a=0,但a不是该方程的根
答案 A ∵(x-m)(x-a)=0,∴x-m=0或x-a=0,∴x1=m,x2=a,∵x1=x2=m,∴m=a,且a是该方程的根,故选A.
2.(2018泉州晋江质检,9)若2a+3c=0,则关于x的一元二次方程ax2+bx+c=0(a≠0)的根的情况是 ( )A.方程有两个相等的实数根B.方程有两个不相等的实数根C.方程必有一根是0D.方程没有实数根
3.(2020福州一检,6)若抛物线y=x2+bx的对称轴是直线x=2,则方程x2+bx=5的解是 ( )A.x1=1,x2=5 B.x1=1,x2=-5C.x1=-1,x2=5 D.x1=-1,x2=-5
4.(2019漳州二检,9)若x=2是关于x的一元一次方程ax-2=b的解,则3b-6a+2的值是 ( )A.-8 B.-4 C.8 D.4
答案 B ∵x=2是关于x的方程ax-2=b的解,∴2a-2=b,即b-2a=-2.∴3b-6a+2=3(b-2a)+2=-6+2=-4.故选B.
5.(2019泉州晋江质检,9)若x2-2px+3q=0的两根分别是-3与5,则多项式2x2-4px+6q可以分解为 ( )A.(x+3)(x-5) B.(x-3)(x+5)C.2(x+3)(x-5) D.2(x-3)(x+5)
解析 由x2+2x-1=0可知a=1,b=2,c=-1,∴m+n=-2,mn=-1,∴m2n+mn2=mn(m+n)=-1×(-2)=2,故答案为2.
7.(2020南平一检,21)商场某品牌童装平均每天可售出20件,每件盈利40元.为了迎接春节,商场决定采取 适当的降价措施,增加盈利,减少库存.经市场调查发现,如果每件童装降价2元,那么平均每天就可多售出 4件.(1)如果平均每天销售这种童装盈利1 200元,那么每件童装应降价多少元?(2)当盈利最多时,每件童装应降价多少元?
人教版中考数学总复习第二章方程(组)与不等式(组)第8课时不等式与不等式组课件: 这是一份人教版中考数学总复习第二章方程(组)与不等式(组)第8课时不等式与不等式组课件,共28页。PPT课件主要包含了答案C等内容,欢迎下载使用。
数学中考复习考点研究 第二章 方程(组)与不等式(组) 命题点1 一次方程(组)的解法(必考) PPT课件: 这是一份数学中考复习考点研究 第二章 方程(组)与不等式(组) 命题点1 一次方程(组)的解法(必考) PPT课件,共18页。PPT课件主要包含了要点归纳,等式的性质,2两种消元法,随堂练习等内容,欢迎下载使用。
中考数学复习第二章方程(组)与不等式(组)过关训练课件: 这是一份中考数学复习第二章方程(组)与不等式(组)过关训练课件,共24页。PPT课件主要包含了<m<1,x=3等内容,欢迎下载使用。












