




【原创】2022届高三二轮专题卷 数学(一)平面向量【学生版+教师版】
展开
这是一份【原创】2022届高三二轮专题卷 数学(一)平面向量【学生版+教师版】,文件包含原创2022届高三二轮专题卷数学一平面向量学生版docx、原创2022届高三二轮专题卷数学一平面向量教师版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
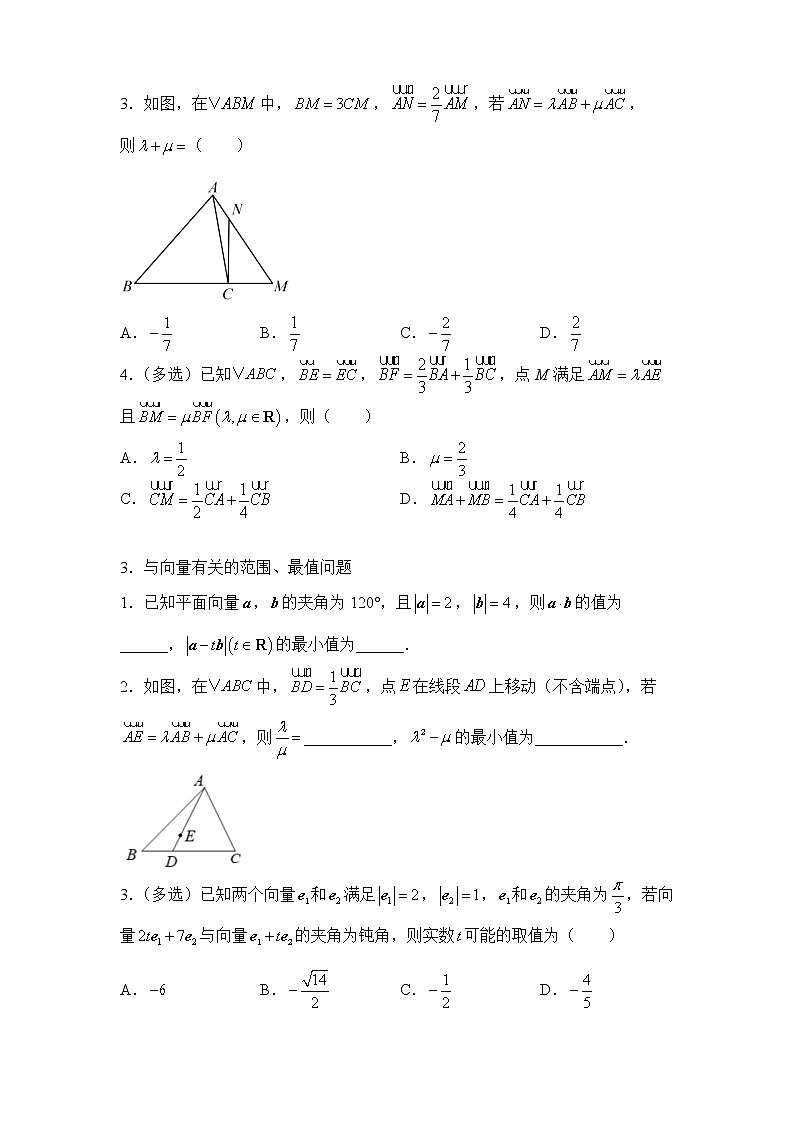
1.与平面向量有关的简单计算1.已知平面向量,,若,则_________.【答案】【解析】因为,则,可得,故,因此,故答案为.2.已知平面向量,,若,则实数的值为( )A.10 B.8 C.5 D.3【答案】A【解析】因为,,所以.因为,所以,解得,故选A.3.如图,A,B,C三点不共线,O为平面ABC外一点,且平面ABC中的小方格均为单位正方形,,,则( )A.1 B. C.2 D.【答案】B【解析】因为,所以,故选B.4.已知为平面上的动点,,为平面上两个定点,且,则动点的轨迹方程为_______.【答案】【解析】设,则,,因为,所以,化简得,所以动点的轨迹方程为,故答案为.5.已知,,,则向量与向量的夹角为______.【答案】【解析】设向量与向量的夹角为,∵,∴,又∵,∴,∵,∴,∴,∴,∵,∴.故答案为.6.已知向量和的夹角为150°,且,,则在上的投影为___________.【答案】或【解析】由,得,因为向量和的夹角为150°,且,所以,得,,所以或,当时,在上的投影为,当时,在上的投影为,综上,在上的投影为或,故答案为或.7.如图,在中,为中线上一点,且,过点的直线与边,分别交于点,.(1)用向量,表示;(2)设向量,,求的值.【答案】(1);(2).【解析】(1)∵为中线上一点,且,∴.(2)∵,,,∴,又,,三点共线,∴,解得,故的值为. 2.向量的线性运算1.已知四边形的对角线交于点O,E为的中点,若,则( )A. B. C. D.1【答案】A【解析】由已知得,,故,又B,O,D共线,故,所以,故选A.2.如图,等腰梯形中,,点为线段上靠近的三等分点,点为线段的中点,则( )A. B. C. D.【答案】B【解析】由题可得,故选B.3.如图,在中,,,若,则( )A. B. C. D.【答案】D【解析】,所以,,故选D.4.(多选)已知,,,点M满足且,则( )A. B.C. D.【答案】AC【解析】,三点共线且为中点,,,,三点共线且为上靠近A的三等分点,,,,,,,A正确,B错误;,C正确;,D不正确,故选AC. 3.与向量有关的范围、最值问题1.已知平面向量,的夹角为120°,且,,则的值为______,的最小值为______.【答案】,【解析】因为平面向量,的夹角为120°,且,,所以,,所以当时,的最小值为,故答案为,.2.如图,在中,,点在线段上移动(不含端点),若,则___________,的最小值为___________.【答案】2,【解析】因为在中,,所以,即.因为点在线段上移动(不含端点),所以设.所以,对比可得.代入,得;代入可得,根据二次函数性质知当时,,故答案为.3.(多选)已知两个向量和满足,,和的夹角为,若向量与向量的夹角为钝角,则实数可能的取值为( )A. B. C. D.【答案】AD【解析】因为,,和的夹角为,所以,因为向量与向量的夹角为钝角,所以,且不能共线,所以,解得,当向量与向量共线时,有,即,解得,所以实数的取值范围,所以实数可能的取值为A,D,故选AD.4.点M在边长为2的正三角形内(包括边界),满足,则的取值范围是( )A. B. C. D.【答案】B【解析】因为点M是正三角形内的一点(包括边界),所以,由,故选B.5.如图所示,已知点G是△ABC的重心,过点G作直线分别交AB,AC两边于与M,N(三角形顶点不重合)两点,且,,则2x+y的最小值为( )A. B. C. D.【答案】A【解析】因为是△ABC的重心,所以,又,,所以,因为三点共线,所以,即,显然,,所以,当且仅当,即,时,等号成立,所以的最小值是,故选A.6.已知、、是平面向量,是单位向量. 若,,则的最大值为_______.【答案】【解析】因为,则,即,因为,即,作,,,,则,,则,固定点,则为的中点,则点在以线段为直径的圆上,点在以点为圆心,为半径的圆上,如下图所示:,设,则,因为,,故,当时,等号成立,即的最大值为,故答案为.7.已知圆O的方程为,P是圆上一点,过P作圆O的两条切线,切点分别为A、B,则的取值范围为____________.【答案】【解析】如图,设PA与PB的夹角为2α,则,∴.P是圆上一点,,,,令,则在上递减,所以当时,,此时P的坐标为,当时,,此时P的坐标为,∴的范围为,故答案为.8.已知圆的半径为3,,为该圆的两条切线,为切点,则的最小值为___________.【答案】【解析】如图所示,设(),,则,,,,当且仅当,即时等号成立,∴的最小值是,故答案为. 4.与其他知识综合1.已知数列的首项为1,又,其中点O在直线l外,其余三点A,B,C均在l上,那么数列的通项公式是( )A. B. C. D.【答案】C【解析】因为,所以,又因为点O在直线l外,三点A,B,C均在l上,故,即,所以,即数列是以为首项,以2为公比的等比数列,故,则,故选C.2.四边形为梯形,且,,,点是四边形内及其边界上的点.若,则点的轨迹的长度是( )A. B. C. D.【答案】B【解析】,即.设向量与的夹角为,则,因为,所以,由向量投影定义得,向量在向量上的投影为2,即动点在过点且垂直于的直线上.在中,,,,由余弦定理得,所以;则,所以.因为是四边形内及其边界上的点,所以点的轨迹为线段,所以点的轨迹的长度为,故选B.
相关试卷
这是一份【原创】2022届高三二轮专题卷 数学(二十)函数与方程【学生版+教师版】,文件包含原创2022届高三二轮专题卷数学二十函数与方程学生版docx、原创2022届高三二轮专题卷数学二十函数与方程教师版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
这是一份【原创】2022届高三二轮专题卷 数学(十九)函数的性质【学生版+教师版】,文件包含原创2022届高三二轮专题卷数学十九函数的性质学生版docx、原创2022届高三二轮专题卷数学十九函数的性质教师版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份【原创】2022届高三二轮专题卷 数学(十六)轨迹方程的求法【学生版+教师版】,文件包含原创2022届高三二轮专题卷数学十六轨迹方程的求法学生版docx、原创2022届高三二轮专题卷数学十六轨迹方程的求法教师版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。








