数学八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定评优课课件ppt

这是一份数学八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定评优课课件ppt，文件包含《1812平行四边形的判定第2课时》同步精品课件pptx、《1812平行四边形判定第2课时》同步精品教案doc等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。
1.探究平行四边形的第四个判定定理。（重点）2.会综合运用平行四边形的性质和判定进行推理和计算。（难点） 3.经历平行四边形判定定理的探索过程，发展合情推理的意识和表述能力，体会几何思维的真正内涵； 4.经历平行四边形的判定定理的探索过程，培养协作、探究精神.
你能说出我们已学的平行四边形的判定方法有哪些吗？
问题：我们知道两组对边平行或相等的四边形是平行四边形， 如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢？
猜想1：一组对边平行的四边形是平行四边形吗？
猜想2：一组对边相等的四边形是平行四边形吗？
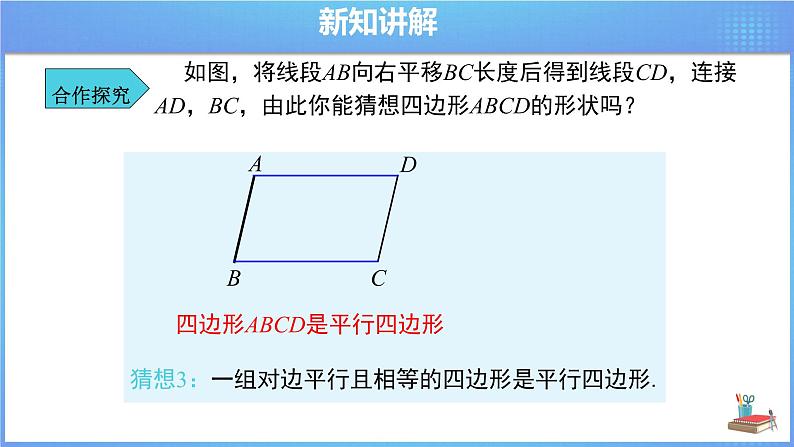
如图，将线段AB向右平移BC长度后得到线段CD，连接AD，BC，由此你能猜想四边形ABCD的形状吗？
四边形ABCD是平行四边形
猜想3：一组对边平行且相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
已知：如图，四边形ABCD中，AB//CD，ABCD．求证：四边形ABCD是平行四边形．
证明：连接AC. ∵AB//CD，∴12. 又∵ABCD，ACCA， ∴△ABC≌△CDA. ∴BCDA. ∴四边形ABCD的两组对边分别相等，它是平行四边形.
平行四边形的判定定理4：一组对边平行且相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AB∥CD，AB=CD,∴四边形ABCD是平行四边形.
现在你学了几种平行四边形的判定方法？
如图，在四边形ABCD中，已知AB//CD，那么再添加条件“ ”，使得四边形ABCD是一个平行四边形．
答案不唯一，言之有理即可.
例 如图，在▱ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形．
证明：∵四边形ABCD是平行四边形， ∴ABCD，EB//FD. 又∵EB AB，FD CD. ∴EBFD. ∴四边形EBFD是平行四边形.
1.能判定一个四边形是平行四边形的条件是( ) A.一组对边平行，另一组对边相等 B.一组对边平行，一组对角互补 C.一组对角相等，一组邻角互补 D.一组对角相等，另一组对角互补
2.如图，E，F分别是▱ABCD的边AB，CD的中点，则图中平行四边形的个数共有( ).
A.2个 B.3个C.4个 D.5个
3.如图，四边形AEFD和EBCF都是平行四边形. 求证：四边形ABCD是平行四边形.
证明：∵四边形AEFD是平行四边形， ∴AD//EF，ADEF. ∵四边形EBCF是平行四边形， ∴BC//EF，BCEF. ∴AD//BC，ADBC， ∴四边形ABCD是平行四边形.
4.如图，在▱ABCD中，E，F分别在边BA，DC的延长线上，已知AECF， P，Q分别是DE，FB的中点，求证：四边形EQFP是平行四边形.
证明：∵四边形ABCD是平行四边形， ∴AB//CD，ABCD. ∵AECF. ∴ABAECDCF，即BEDF. 又∵BE//DF. ∴四边形BEDF是平行四边形. ∴DE//BF，DEBF. ∵P，Q分别是DE，FB的中点. ∴EP//QF，EP DE BFQF. ∴四边形EQFP是平行四边形.
两组对边分别平行的四边形是平行四边形.
1.两组对边分别相等的四边形是平行四边形. 2.两组对角分别相等的四边形是平行四边形. 3.对角线互相平分的四边形是平行四边形. 4.一组对边平行且相等的四边形是平行四边形.
1.平行四边形的判定方法
（1）定义：两组对边分别平行的四边形是平行四边形.
（2）四个判定定理 ①两组对边分别相等的四边形是平行四边形. ②两组对角分别相等的四边形是平行四边形. ③对角线互相平分的四边形是平行四边形. ④一组对边平行且相等的四边形是平行四边形.
教科书第47页练习4习题18.1第4题