初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定获奖ppt课件

这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定获奖ppt课件，文件包含《1812平行四边形的判定第3课时》同步精品课件pptx、《1812平行四边形的判定第3课时》同步精品教案doc等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
1.理解三角形中位线的概念，掌握三角形的中位线定理；(重点）2.能较熟练地应用三角形中位线的性质进行有关的证明和计算；（难点）3.经历观察、操作、猜想、证明的过程，进一步发展推理论证的能力；4.在推理论证的过程中感悟多种证明思路和转化、化归的数学思想.
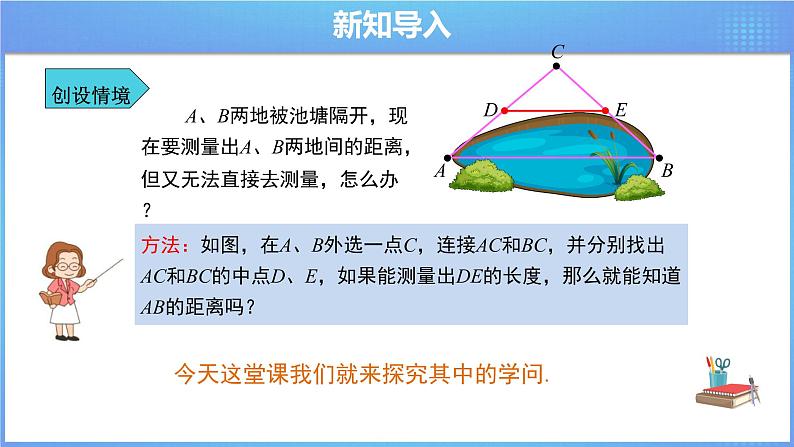
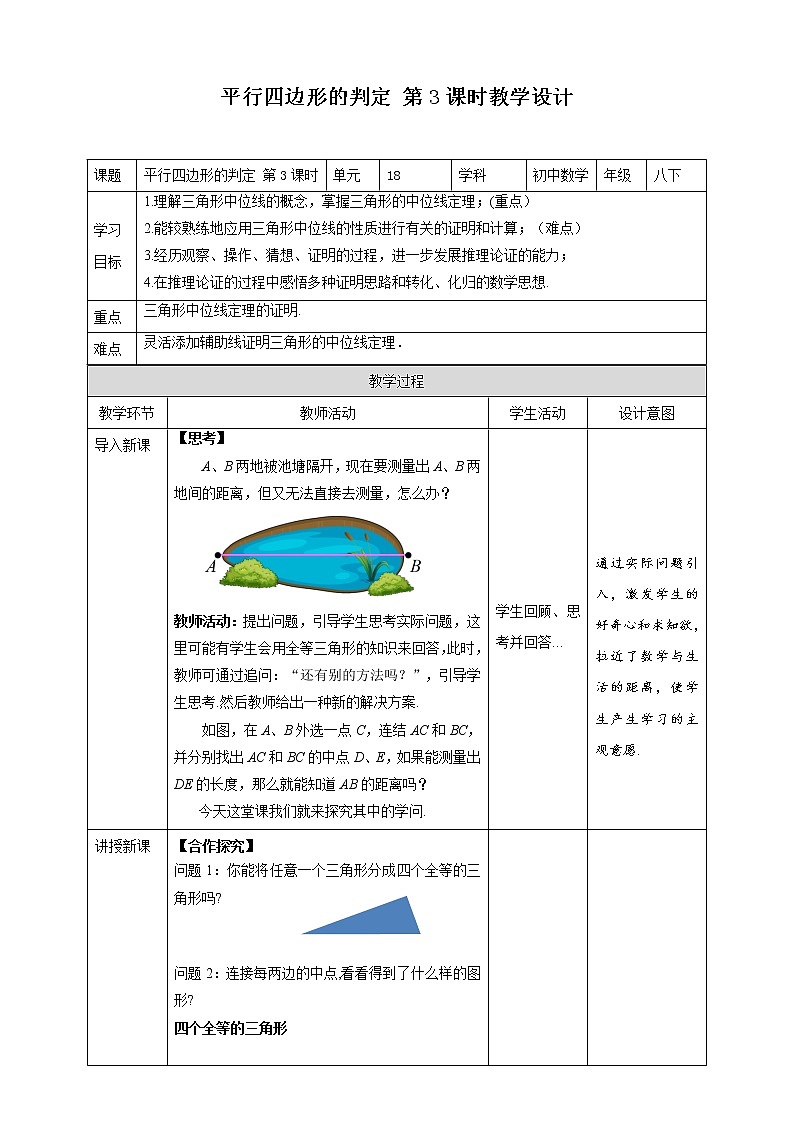
A、B两地被池塘隔开，现在要测量出A、B两地间的距离，但又无法直接去测量，怎么办？
方法：如图，在A、B外选一点C，连接AC和BC，并分别找出AC和BC的中点D、E，如果能测量出DE的长度，那么就能知道AB的距离吗？
今天这堂课我们就来探究其中的学问.
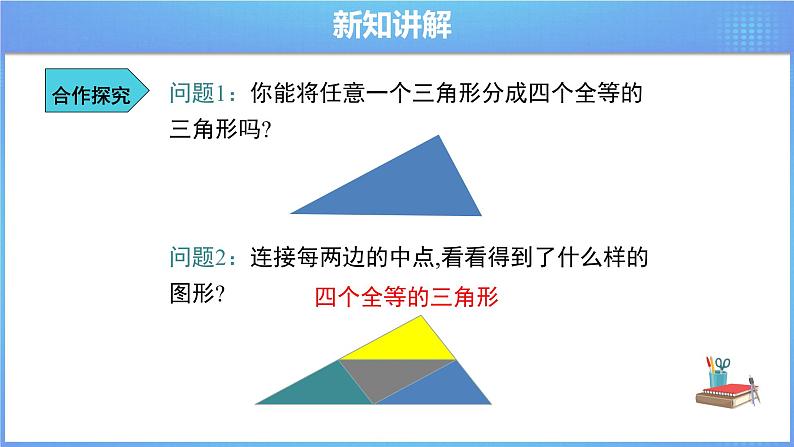
问题1：你能将任意一个三角形分成四个全等的三角形吗?
问题2：连接每两边的中点,看看得到了什么样的图形?
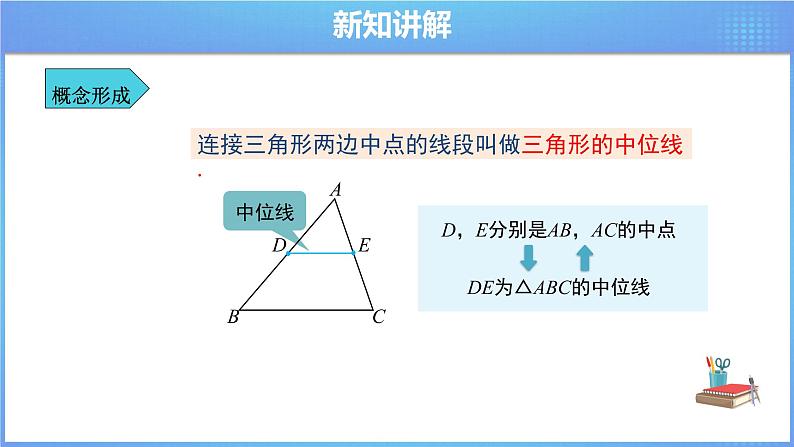
D，E分别是AB，AC的中点
DE为△ABC的中位线
连接三角形两边中点的线段叫做三角形的中位线.
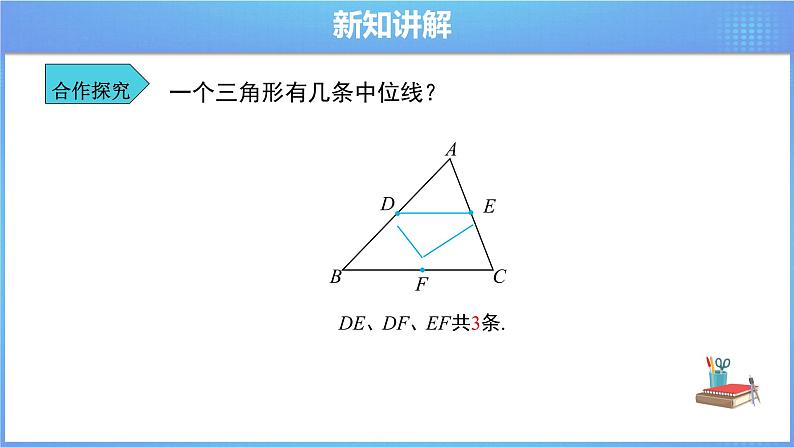
一个三角形有几条中位线？
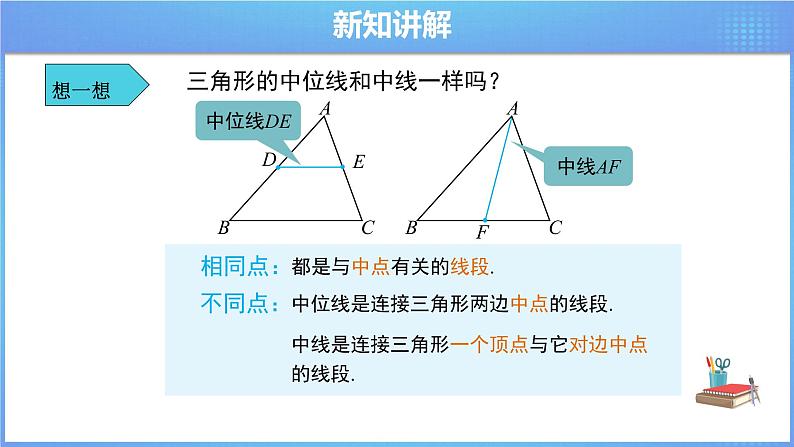
三角形的中位线和中线一样吗？
都是与中点有关的线段.
中位线是连接三角形两边中点的线段.
中线是连接三角形一个顶点与它对边中点的线段.
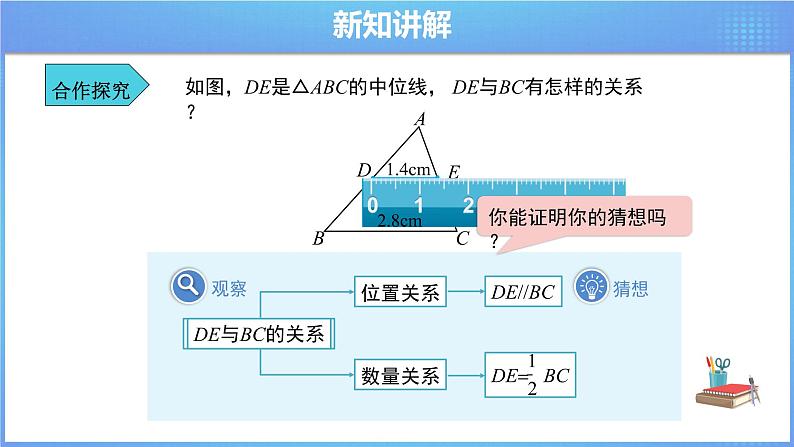
如图，DE是△ABC的中位线， DE与BC有怎样的关系？
证明：延长DE到F，使EFDE，连接FC，DC，AF. ∵AECE，DEEF. ∴四边形ADCF是平行四边形. ∴CF//DA，CFDA. ∴CF BD. ∴四边形DBCF是平行四边形. ∴DF BC.
又∵DE DF. ∴DE//BC， 且DE BC.
证明：延长DE到F，使EFDE，连接FC. ∵AECE，AEDCEF，DEEF. ∴△ADE≌△CFE. ∴ADCF，AFCE. ∴AB//FC.
∴四边形BCFD是平行四边形.
三角形的中位线平行于三角形的第三边，并且等于第三边的一半.
①证明平行问题.②证明一条线段是另一条线段的两倍或一半.
1.如图1，在△ABC中，DE是中位线 (1)若ADE60°，则B 度； (2)若BC=8cm，则DE cm.
2.如图2，在△ABC中，D、E、F分别是 各边中点.EF3cm，DF4cm，DE5cm， 则△ABC的周长 cm.
例 如图，点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点.求证：四边形EFGH是平行四边形．
证明：连接AC．在△ABC中， ∵点E，F分别是边AB，BC的中点， ∴EF//AC，EF AC． 同理，GH//AC，GH AC． ∴EF//GH，且EFGH． ∴四边形EFGH是平行四边形．
1.如图，在▱ABCD中，对角线AC，BD交于点O，E为边BC的中点，连接OE，若AB4，则OE .
2.△ABC中，ABAC，AD是BC边上的高，E为AB的中点，若BC10，AD12，则DE的长为( ) A.5 B.5.5 C.6 D.6.5
3.△ABC中，点D、E、F分别为边BC、AB、CA的中点，则下列关于线段AD和EF之间关系的说法中正确的是( ) A.ADEF B.ADEF C.AD和EF互相平分 D.以上答案都不对
4.如图，在▱ABCD中， E是CD边的中点，F为AE的中点，连结FC、BE交于点G.求证：GFGC.
证明：取BE的中点H，连结HF、HC. ∵F、H分别是AE、BE的中点.
∵▱ABCD中，E是CD边的中点，
∴四边形EFHC是平行四边形.
连接三角形两边中点的线段叫做三角形的中位线．
三角形的中位线平行于三角形的第三边，并且等于第三边的一半.
（1）定义：连接三角形两边中点的线段叫做三角形的中位线．
（2）定理 三角形的中位线平行于三角形的第三边，并且等于第三边的一半。
教科书第49页练习第3题习题18.1第5题