2021学年7.3* 复数的三角表示课文内容ppt课件

这是一份2021学年7.3* 复数的三角表示课文内容ppt课件，共22页。PPT课件主要包含了复数的代数形式，复数a+bi，复数的辐角，辐角主值等内容，欢迎下载使用。

i 叫做虚数单位，并且规定： (1) i 21； (2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立.
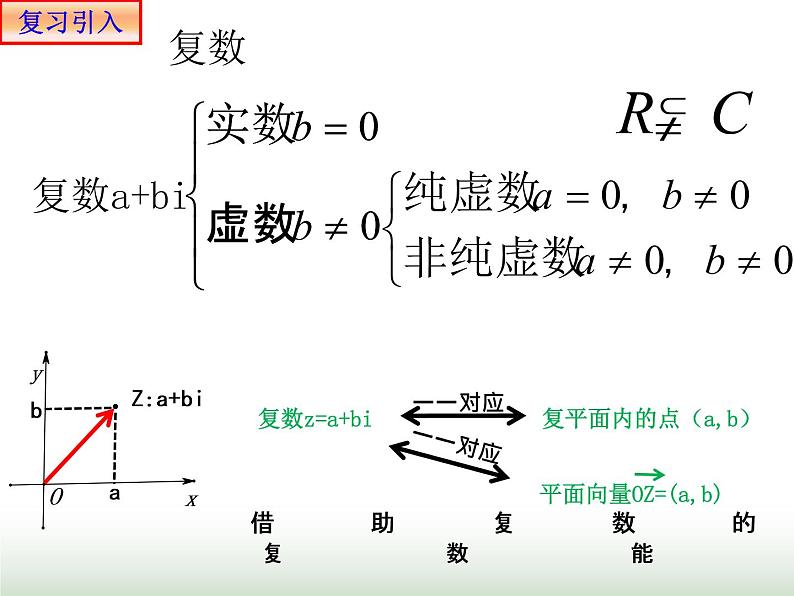
复平面内的点（a,b）
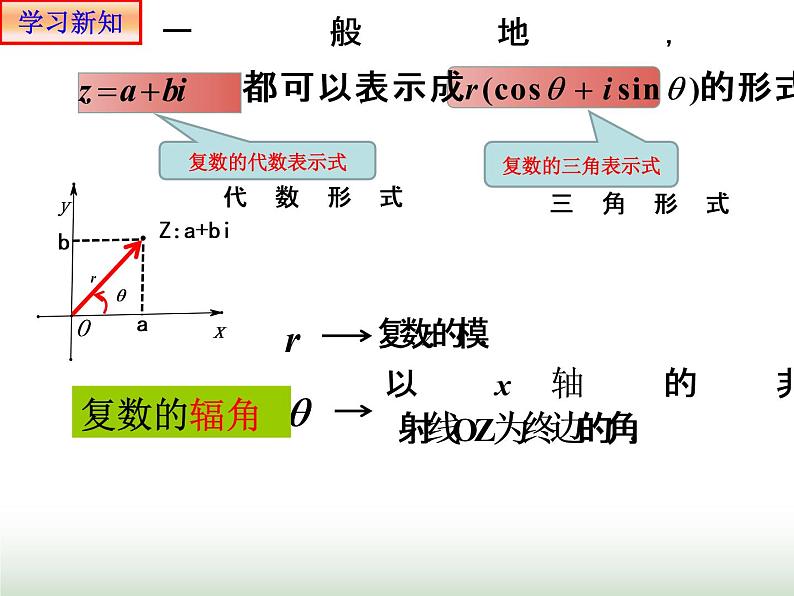
3.写出复数的三角形式
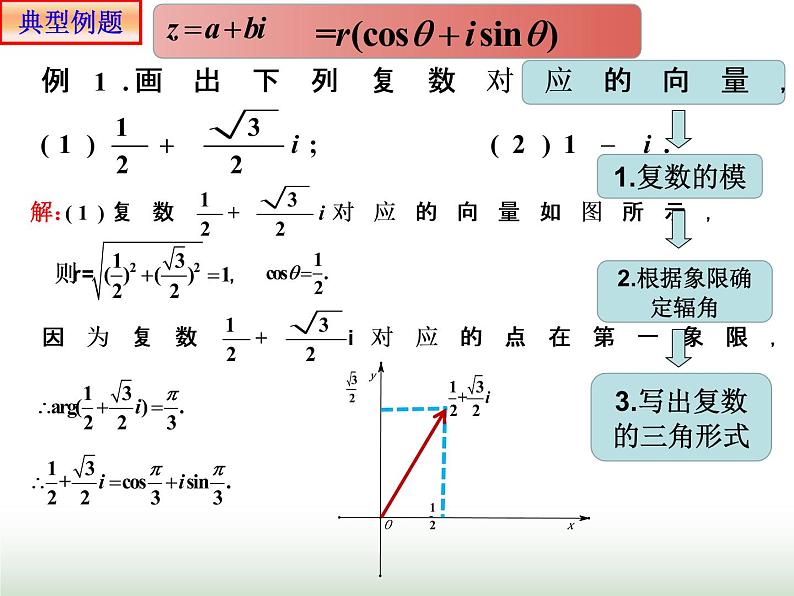
将下列复数表示成三角形式.(1)5i　　(2)8　　(3)-3-3i　　(4)-1+ i
两个非零复数相等当且仅当它们的模与辐角的主值分别相等
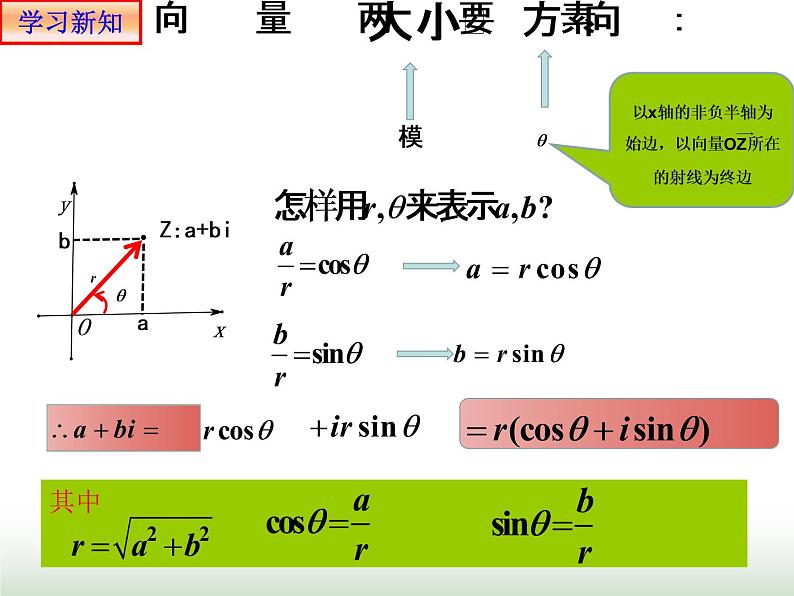
思考：两个用三角形式表示的复数在什么条件下相等？
解题技巧(复数三角形式的判断依据和变形步骤)
(1)判断依据：三角形式的结构特征：模非负，角相同，余弦前，加号连．(2)变形步骤：首先确定复数z对应点所在象限(此处可假定θ为锐角)，其次判断是否要变换三角函数名称，最后确定辐角．此步骤可简称为“定点→定名→定角”.
2(cs 260°＋isin 260°)
3．复数－2(sin 10°＋ics 10°)的三角形式为___________
2．两个复数z1、z2的模与辐角分别相等，是z1＝z2成立的( ) A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分又不必要条件
若z∈C,|z-2|≤1,求|z|的最大、最小值和argz范围.
数形结合思想求复数的模长及辐角范围
分析:结合条件及特点,本题可用数形结合思想求解.