



人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系课前预习课件ppt
展开
这是一份人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系课前预习课件ppt,共22页。PPT课件主要包含了异面直线的定义,α∥β,归纳总结,a∥b,aIbA等内容,欢迎下载使用。
前面我们认识了空间中点、直线、平面之间的一些位置关系,如点在平面内,直线在平面内,两个平面相交,等等,空间中点、直线、平面之间还有其他位置关系吗?空间中点与直线的位置关系有两种:点在直线上和点在直线外. 空间中点与平面的位置关系也有两种:点在平面内和点在平面外
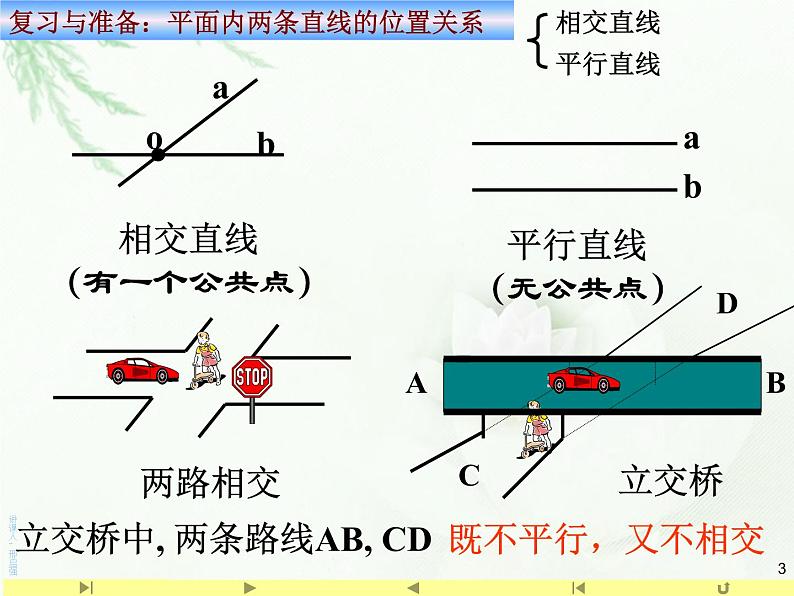
复习与准备:平面内两条直线的位置关系
相交直线(有一个公共点)
立交桥中, 两条路线AB, CD
两直线异面的判别二 : 两条直线不同在任何一个平面内.
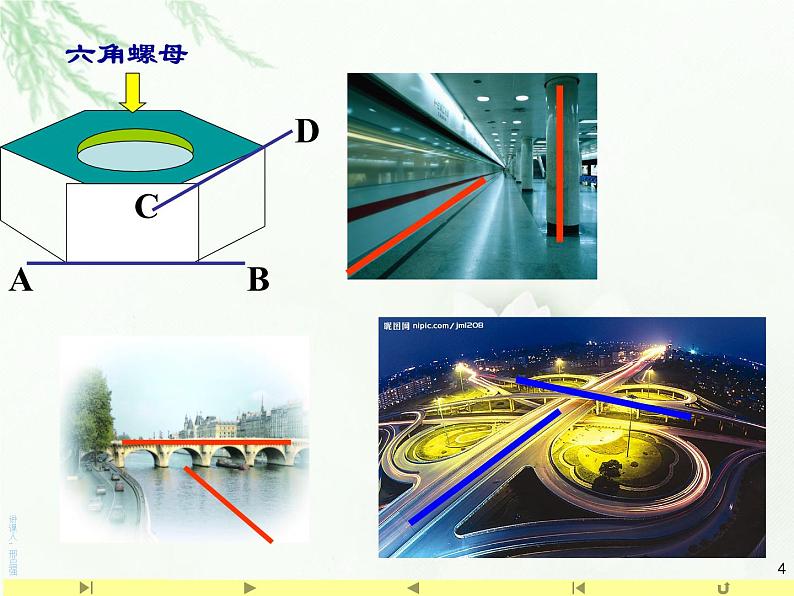
不同在 任何 一个平面内的两条直线叫做异面直线。
两直线异面的判别一 : 两条直线 既不相交、又不平行.
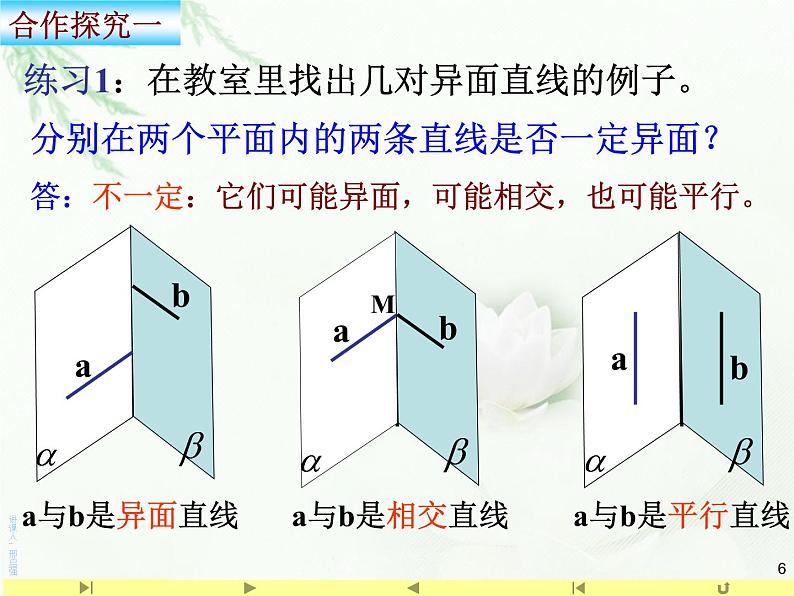
答:不一定:它们可能异面,可能相交,也可能平行。
分别在两个平面内的两条直线是否一定异面?
练习1:在教室里找出几对异面直线的例子。
在同一个平面内,有且只有一个公共点:
空间中直线与直线之间的位置关系
在同一个平面内,没有公共点:
不同在任何一个平面内,没有公共点:
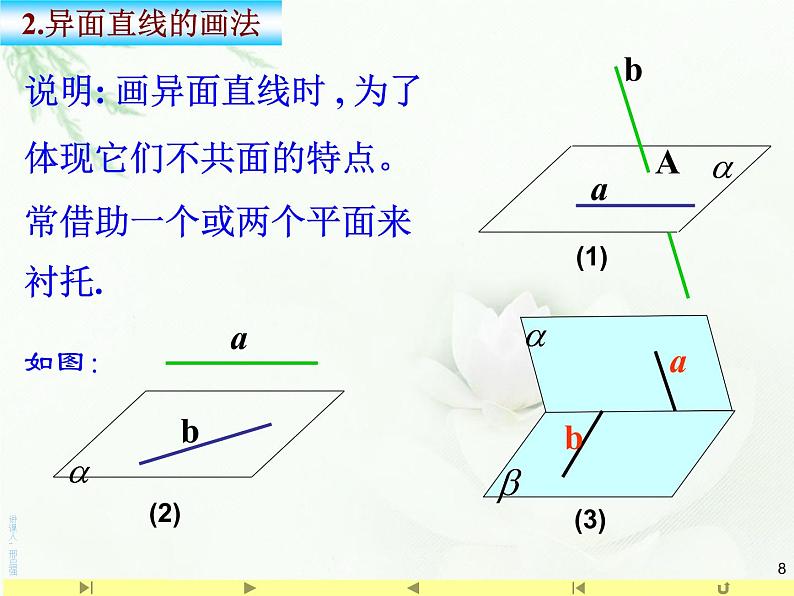
说明: 画异面直线时 , 为了体现它们不共面的特点。常借助一个或两个平面来衬托.
如图是一个正方体的展开图,如果将它还原为正方体, 那么 AB , CD , EF , GH 这四条线段所在直线是异面直线的有 对?
答:共有三对AB与CDAB与GHEF与GH
直线上所有的点都在平面内直线在平面内
直线与平面有一个公共点直线与平面相交
直线与平面无公共点直线与平面平行
我们常把直线与平面相交或平行的情况称为直线在平面外。记作
空间中线与面的位置关系
(2)若l // a,则直线l 与平面a内任一条直线都平行
(1)若直线l上有无数个点不在平面a内,则l // a
(4)若l // a ,则直线l 与平面a内任意一条直线都没有公共点
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
例2、若直线a不平行平面 ,且
则下列结论成立的是( )
(A) 内所有直线与a异面(B) 内不存在与a平行的直线(C) 内存在唯一的直线与a平行(D) 内的直线与a都相交
复习:公理3
若两个不重合平面有一个公共点,则它们有且只有一条过该点的公共直线。
思考:两平面有哪几种位置关系?如何分类?
空间中面与面的位置关系
两个平面有一公共直线两个平面相交
两个平面无公共点两个平面平行
α β=L,a α=A, a β=B
例1 由下图,分别用文字和符号语言表示下列图形中点、直线和平面的位置关系。
直线a分别交平面α、 β于点A、B,平面α和β相交与直线L
平面α与β相交于直线L,直线a在平面α内,直线b在平面β内,直线a和b相交于点P
a α ,b β,α β=L,a b=P,P∈L
一个长方体切一刀可以分成多少块?一个长方体切两刀可以分成多少块?一个长方体切三刀可以分成多少块?
1、一个平面把空间分为几部分?2、二个平面把空间分为几部分?3、三个平面把空间分为几部分?
例3:已知a ∥β,则直线a和直线b的位置关系如何?
(1)空间中点与线、点与面的位置关系
(2)空间中线与线的位置关系
两直线不共面且无公共点两直线异面
两直线共面且有一个公共点两直线相交
两直线共面且无公共点两直线平行
(3)空间中线与面的位置关系
(4)空间中面与面的位置关系
相关课件
这是一份人教A版 (2019)必修 第二册第八章 立体几何初步8.4 空间点、直线、平面之间的位置关系授课课件ppt,共20页。
这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系教学演示ppt课件,共20页。
这是一份2020-2021学年8.4 空间点、直线、平面之间的位置关系示范课课件ppt,文件包含842空间点直线平面之间的位置关系pptx、842分层演练综合提升docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。










