高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用背景图ppt课件

这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用背景图ppt课件，共18页。PPT课件主要包含了复习引入，新课引入，实际问题，解应用题的基本思路，学习新知，变式练习，问题探究，问题解决，形成规律，巩固练习等内容，欢迎下载使用。
1.正弦定理和余弦定理的基本公式是什么？
①已知三角形的任意两角及其一边； ②已知三角形的任意两边与其中一边 的对角.
2. 运用正弦定理能解怎样的三角形？
①已知三边求三角；②已知两边及它们的夹角，求第三边.③已知三角形的任意两边与其中一边 的对角.
3. 运用余弦定理能解怎样的三角形？
我国的嫦娥2号成功绕月飞行， “遥不可及的月亮离我们地球究竟有多远呢？” 在古代，天文学家没有先进的仪器就已经估算出了两者的距离，是什么神奇的方法探索到这个奥秘的呢？我们知道，对于未知的距离、高度等，存在着许多可供选择的测量方案，比如可以应用全等三角形、相似三角形的方法，或借助解直角三角形等等不同的方法，但由于在实际测量问题的真实背景下，某些方法会不能实施。如因为没有足够的空间，不能用全等三角形的方法来测量，所以，有些方法会有局限性。于是上面介绍的问题是用以前的方法所不能解决的。今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用，首先研究如何测量距离。
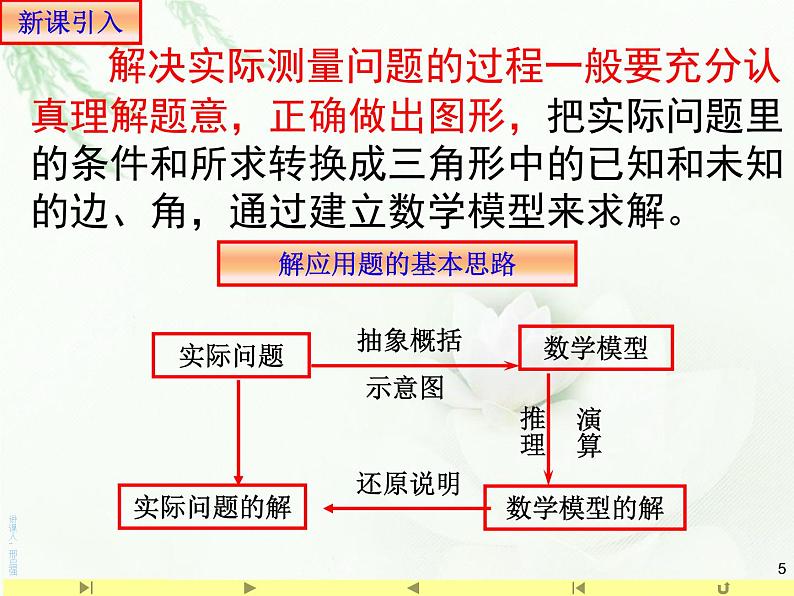
解决实际测量问题的过程一般要充分认真理解题意，正确做出图形，把实际问题里的条件和所求转换成三角形中的已知和未知的边、角，通过建立数学模型来求解。
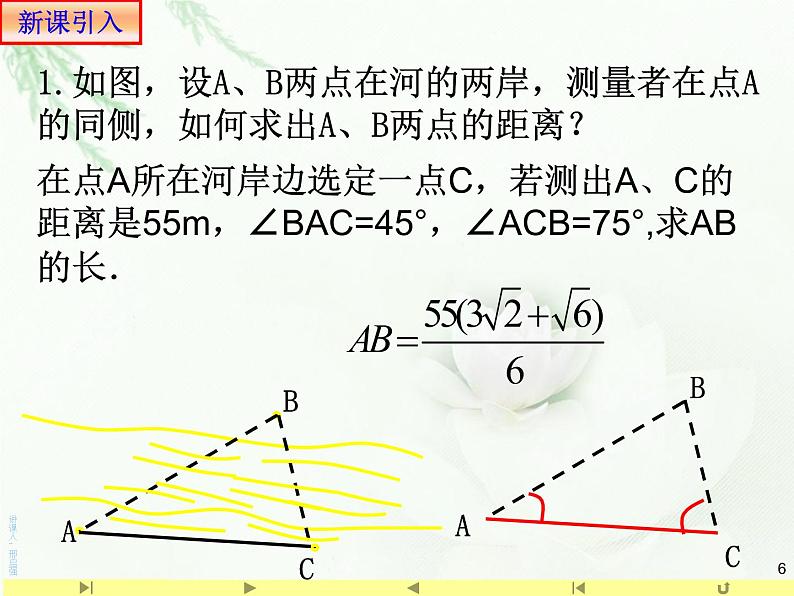
1.如图，设A、B两点在河的两岸，测量者在点A的同侧，如何求出A、B两点的距离？
在点A所在河岸边选定一点C，若测出A、C的距离是55m，∠BAC=45°，∠ACB=75°,求AB的长．
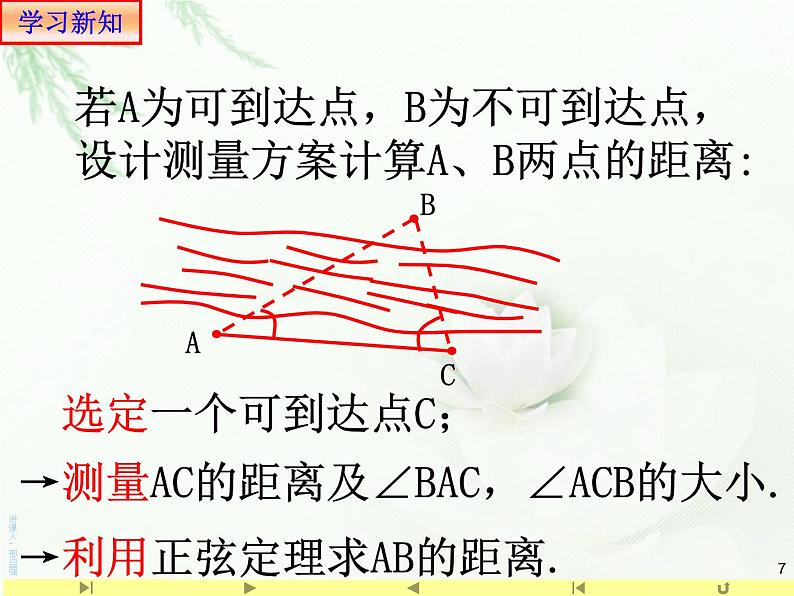
若A为可到达点，B为不可到达点，设计测量方案计算A、B两点的距离:
选定一个可到达点C；
→测量AC的距离及∠BAC，∠ACB的大小.
→利用正弦定理求AB的距离.
两灯塔A、B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东30，灯塔B在观察站C南偏东60，则A、B之间的距离为多少？
2.设A、B两点都在河的对岸（不可到达），你能设计一个测量方案计算A、B两点间的距离吗？
测量者可以在河岸边选定两点C、D，测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.
解：测量者可以在河岸边选定两点C、D，测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中，应用正弦定理得
计算出AC和BC后，再在⊿ABC中，应用余弦定理计算出AB两点间的距离
若测得∠BCD＝∠ADB＝45°，∠ACB＝75°,∠ADC＝30°,且CD＝ ，试求A、B两点间的距离．
解：在△ACD中，∠DAC=180°－(∠ACD+∠ADC)=180°－(75°+45°+30°)=30°∴AC=CD=
在△BCD中，∠CBD=180°－（∠BCD+∠BDC）=180°－(45°+45°+30°）=60°
由正弦定理 ， 得
在△ABC中由余弦定理，
所求A、B两地间的距离为　　　米。
选定两个可到达点C、D；
→测量C、D间的距离及∠ACB、∠ACD、∠BDC、∠ADB的大小；
→利用正弦定理求AC和BC；
→利用余弦定理求AB.
测量两个不可到达点之间的距离方案：
练习：在山下A处用激光测距仪测出到两座山峰B、C的距离分别是2500m和2350m，从A处观察这两目标的视角是135，B、C两山峰相距多远？
2．如图，甲船以每小时
向正北方航行，乙船按固定方向匀速直线航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，此时两船相距20海里，当甲船航行20分钟到达A2处时，乙船航行到甲船的北偏西120°方向的B2处时，此时两船相距 海里，问乙船每小时航行多少海里？
在测量上，根据测量需要适当确定的线段叫做基线,如例1中的AC，例2中的CD.基线的选取不唯一，一般基线越长，测量的精确度越高.
解斜三角形应用题的一般步骤：
（1）分析：理解题意，分清已知与未知， 画出示意图
（2）建模：根据已知条件与求解目标，把已知量与求解量尽量集中在有关的三角形中，建立一个解斜三角形的数学模型
（3）求解：利用正弦定理或余弦定理有序地 解出三角形，求得数学模型的解
（4）检验：检验上述所求的解是否符合实际 意义，从而得出实际问题的解