资料中包含下列文件,点击文件名可预览资料内容




还剩6页未读,
继续阅读
所属成套资源:2022年七年级数学寒假辅导专题讲义(人教版)
成套系列资料,整套一键下载
专题01 掌握三大技能,轻松解答数轴动态问题 2022年七年级数学寒假辅导讲义(人教版)
展开
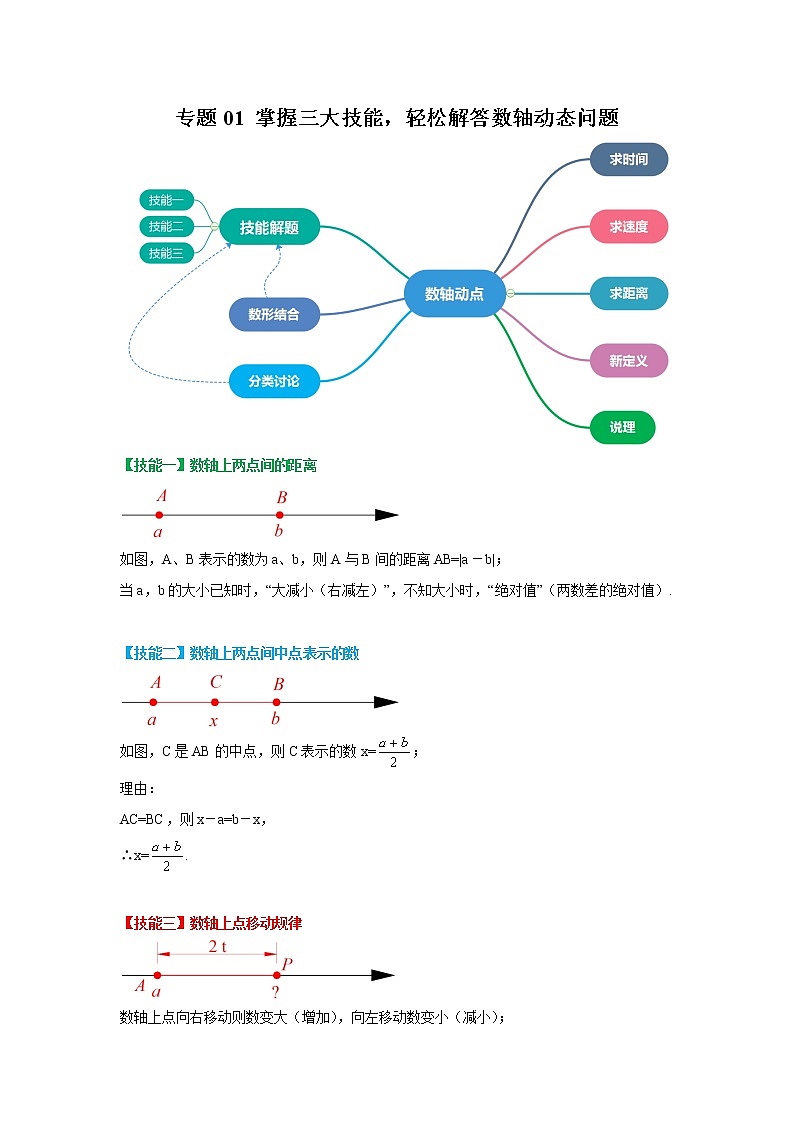
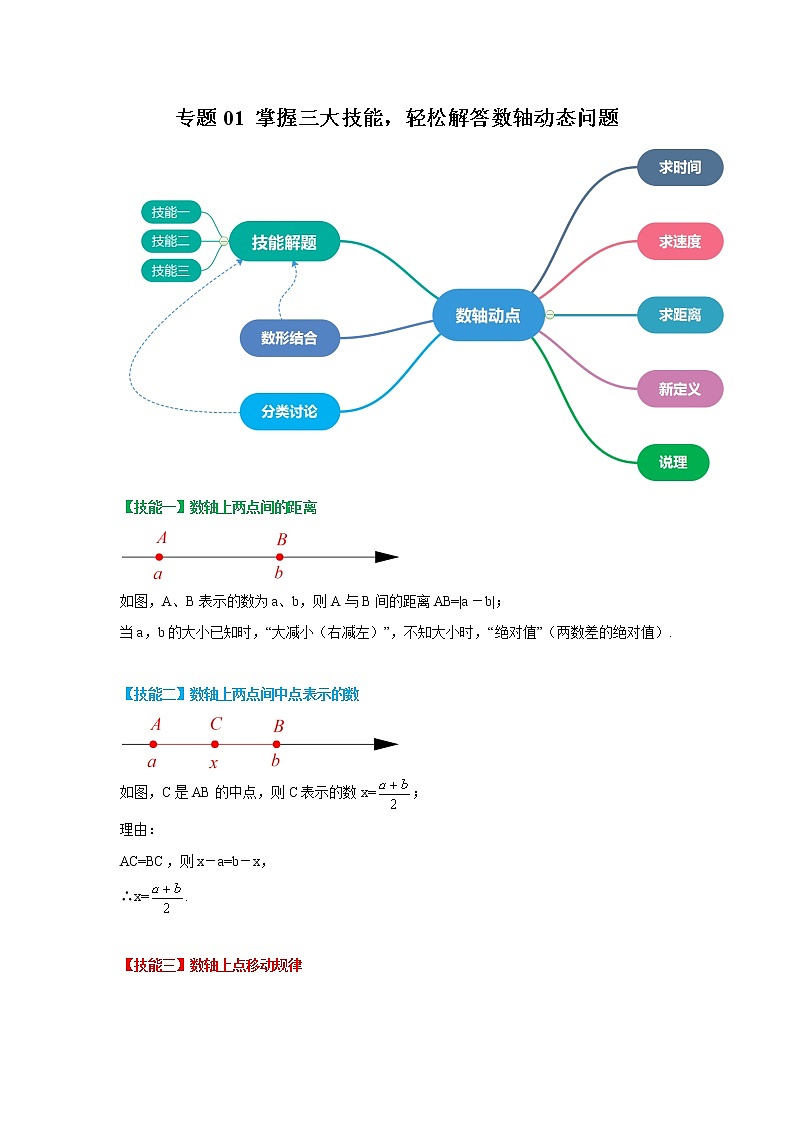
专题01 掌握三大技能,轻松解答数轴动态问题
【技能一】数轴上两点间的距离
如图,A、B表示的数为a、b,则A与B间的距离AB=|a-b|;
当a,b的大小已知时,“大减小(右减左)”,不知大小时,“绝对值”(两数差的绝对值).
【技能二】数轴上两点间中点表示的数
如图,C是AB的中点,则C表示的数x=;
理由:
AC=BC,则x-a=b-x,
∴x=.
【技能三】数轴上点移动规律
数轴上点向右移动则数变大(增加),向左移动数变小(减小);
当数a表示的点向右移动b个单位长度后到达点表示的数为a+b;向左移动b个单位长度后到达点表示的数为a-b.
例:P从A出发,以2个单位/秒速度向右运动,t秒后达到的点表示的数为:a+2t.
数轴是数形结合的产物,分析数轴上点的运动要结合图形进行分析,点在数轴上运动形成的路径可看作数轴上线段的和差关系.
考点一:求动点速度
例1.【2020·龙城期中】已知多项式的常数项是a,次数是b,且a,b两个数轴上所对应的点分别为A、B,若点A、点B同时沿数轴向正方向运动,点A的速度是点B的2倍,且3秒后,,点B的速度为 .
【答案】或.
【解析】解:由题意知a=-4,b=3,
设B点速度为x单位/秒,则A的速度为(2x)单位/秒,
3秒后,A点表示点为-4+3×2x=-4+6x,B点表示的数为3+3x,
∴OA=|-4+6x|,OB=3+3x,
∴|-4+6x|=3+3x,
解得:x=或x=
故答案为:或.
考点二:求动点运动时间
例2.【2020·江苏期中】我们知道:在数轴上,点M表示实数为a,点N表示实数为b,当 时,点M、N之间的距离记作:MN =;当时,点M、N之间的距离记作:MN =a-b,例如:, 则MN =.
如图,点A、B、C是数轴上从左向右依次排列的三点,且,,点B表示的数是.
(1)点A表示的数是 ,点C表示的数是 ;
(2)动点M、N分别从A、C同时出发,点M沿数轴向右运动,速度为1个单位长度∕秒,点N沿数轴向左运动,速度为2个单位长度∕秒,运动t秒后:
①点M表示的数 ,点N表示的数 ;(用含t的代数式表示)
②求当t为何值时,点M、N、B三点中相邻两个点之间的距离相等.(M、N、B三点中任意两点不重合).
【答案】(1)-10, 5;(2)①-10+t,5-2t;②见解析.
【解析】解:(1)∵AC=15,BC=9,
∴AB=6,
∴点A表示的数为-4-6=-10,点C表示的数为-10+15=5.
故答案为:点A表示的数为-10,点C表示的数为5.
(2)设运动时间为t时,
①AM=t,点M表示的数为-10+t;CN=2t,点N表示的数为5-2t,
②分三种情况讨论:
当B为中点时,(-10+t)+(5-2t)=2×(-4),解得t=3;
当N为中点时,(-10+t)+(-4)=2×(5-2t),解得t=4.8;
当M为中点时,(5-2t) +(-4)=2×(-10+t),解得t=5.25;
综上所述,当t为3秒或4.8秒或5.25秒时,点M,N,B三点中相邻两个点之间的距离相等.
例3. 【2020·杭州月考】已知数轴上两点A、B对应的数分别为-1,3,点P为数轴上一动点,其对应的数为x.
(1)若点到点、点的距离相等,则点对应的数为______.
(2)利用数轴探究:找出满足的的所有值是______.
(3)当点以每秒6个单位长的速度从点向右运动时,点以每秒6个单位长的速度向右运动,点以每秒钟5个单位长的速度向右运动,问它们同时出发,几秒后点到点、点的距离相等?
【答案】(1)1;(2)-3或5;(3)2秒或4秒.
【解析】解:(1)∵点P到点A、点B的距离相等
∴x+1=3-x,解得x=1,
即点P表示的数为1.
(2)①当x>3时,
x-3+x+1=8,解得:x=5.
②当x<-1时,
3-x-x-1=8,解得:x=-3.
③当-1≤x≤3时,|x-3|+|x+1|=4≠8,不成立,
∴满足原方程的所有值为:-3或5;
故答案为:-3或-5.
(3)分两种情况:
①当P点在AB之间时.则5x+3-6x=1.解得:x=2
②当P点在AB右侧时,此时A、B重合
则5x+4=6x.解得:x=4
综上所述:它们同时出发,2秒或4秒后P到点A、点B的距离相等.
例4. 【2020·云南官渡期中】如图,数轴上的点和点分别表示0和10,点是线段上一动点.点沿以每秒2个单位的速度往返运动1次,是线段的中点,设点运动时间为秒(不超过10秒).若点在运动过程中,当时,则运动时间的值为
【答案】或或或.
【解析】解:由题意知,B点表示的数为5,
当PB=2时,P点表示的数为3或7,
(1)当P从O到A运动时,PB=2时,则t=或;
(2)当P从A到O运动时,PB=2时,则t=或;
故答案为:或或或.
例5. 【2020·湖北孝感月考】已知数轴上有、两个点对应的数分别是、,且满足;
(1)求、的值;
(2)点是数轴上、之间的一个点,使得,求出点所对应的数;
(3)点,点为数轴上的两个动点,点从点以3个单位长度每秒的速度向右运动,点同时从点以2个单位长度每秒的速度向左运动,设运动时间为秒,若,求时间的值.
【答案】见解析.
【解析】解:(1)∵,
∴a+3=0,b-9=0,
∴a=-3,b=9.
(2)设M点表示的数为x,
∵AM=2BM,
∴x+3=2(9-x)
解得:x=5
即M点表示的数为5.
(3)由题意知,AP=3t,BQ=2t,P点表示的数为3t-3,Q点表示的数为9-2t,
∴PQ=|9-2t-3t+3|=|12-5t|,
∴3t+2t=2|12-5t|,
解得:t=或t=
综上所述,t=或t=时,满足题意.
例6. 【2020·东安实验学校期中】数轴上点A表示的有理数为20,点B表示的有理数为-10,点P从点A出发以每秒5个单位长度的速度在数轴上往左运动,到达点B后立即返回,返回过程中的速度是每秒2个单位长度,运动至点A停止,设运动时间为t(单位:秒).
(1)当t=5时,点P表示的有理数为 .
(2)在点P往左运动的过程中,点P表示的有理数为 (用含t的代数式表示).
(3)当点P与原点距离5个单位长度时,t的值为 .
【答案】(1)-5;(2)20-5t;(3)3;5;8.5;13.5.
【解析】解:(1)由题意得:AB=30,
点P从点A运动到点B所需时间为:30÷5=6秒,
点P从点B返回,运动到点A所需时间为30÷2=15秒,
则当t=5时,PA=25,
∴点P表示的有理数为20-25=-5,
故答案为:-5;
(2)在点P往左运动的过程中,PA=5t,
则点P表示的有理数为20-5t,
故答案为:20-5t;
(3)①当点P从点A运动到点B时,
由(2)可知,,
解得t=3或t=5;
②当点P从点B返回,运动到点A,
由题意知P点表示的数为2(t-6)-10=2t-22,
则,
解得t=8.5或t=13.5
故答案为:3或5或8.5或13.5.
考点三:新定义类型
例7. 阅读理解:若为数轴上三点,若点到的距离是点到的距离2倍,我们就称点是的好点.例如,如图1,点是的好点:点是的好点.
(1)如图2,为数轴上两点,点所表示的数为,点所表示的数为4.在数轴上的好点所表示的数是__________.
(2)如图3,为数轴上两点,点所表示的数为,点所表示的数为40.现有一只电子蚂蚁从点出发,以2个单位每秒的速度向左运动,到达点停止.当为何值时,P、A和中恰有一个点为其余两点的好点?
【答案】(1)0;(2)见解析.
【解析】解:(1)设所求的数为x,根据题意得:
4-x=2(x+2),解得:x=0,
故答案为:0.
(2)设点P表示的数为y,
①当点P为【A,B】的好点,由题意得:
y+20=2(40-y),解得:y=20,
∴t=10 秒;
②当P为【B,A】的好点,由题意得:
40-y=2(y+20),解得y=0,
∴t=20秒
③当B为【A,P】的好点,由题意得:
40+20=2(40-y),解得:y=10,
∴t=(40-10)÷2=15秒;
④当A为【B,P】的好点,由题意得:
40+20=2(y+20),解得:y=10,
∴t=(40-10)÷2=15秒;
综上所述:当t的值为10或15或20时,P、A和B中恰有一个点为其余两点的好点.
例8. 【2019·广州市期中】数轴上有三点,给出如下定义;若其中一个点与其他两个点的距离恰好满足倍的数量关系,则称该点是其它两个点的:“关联点”
(1)例图,数轴上点三点所表示的数分别为,点到点的距离 ,点到点的距离是 ,因为是的两倍,所以称点是点的“关联点”.
(2)若点表示数点表示数,下列各数所对应的点分别是,其中是点的“关联点”的是 ;
(3)点表示数,点表示数为数轴上一个动点;若点在点的左侧,且点是点的“关联点”,求此时点表示的数;若点在点的右侧,点中,有一个点恰好是其它两个点的“关联点”.请直接写出此时点表示的数.
【答案】(1)2,1;(2)C1,C3(3)见解析.
【解析】解:(1)由题意知,AB=3-1=2,BC=4-3=1
故答案是:2,1;
(2)点A表示的数为-2,点B表示的数为1,C1表示的数为-1,
∴AC1=1,BC1=2,
∴C1是点A、B的“关联点”;
同理,C2、C4不是点A、B的“关联点”,C3是点A、B的“关联点”.
故答案为:C1,C3.
(3)①若点P在点B的左侧,且点P是点A,B的“关联点”,设点P表示的数为x
(I) 当P在点A的左侧时,则有:2PA=PB,即2(-10-x)=15-x
解得:x=-35
(II)当点P在A,B之间时,有2PA=PB或PA=2PB
有2(x+10)=15-x或x+10=2(15-x)
解得:x=或x=
∴点P表示的数为-35或或.
②若点P在点B的右侧
(I)若点P是A,B的“关联点”则有2PB=PA
即2(x-15)=x+10
解得:x=40
(II)若点B是A,P的“关联点”则有2AB=PB或AB=2PB
即2(15+10)=x-15或15+10=2(x-15)
解得x=65或x=
(III)若点A是B,P的“关联点”则有2AB=AP
即2(15+10)=x+10
解得x=40
∴点P表示的数为40或65或.
考点四:求动点表示的数
例9.【河北期末】如图,点为数轴的原点,点对应的数为,点对应的数为,且,点为数轴上的动点,且点对应的数为.当时,的值为 .
【答案】7或11.
【解析】解:由题意知,a=-4,b=10,
当x<-4时,PA=-4-x,PB=10-x,
∴-4-x+2(10-x)=17,解得:x=(舍)
当-4≤x≤10时,x+4+2(10-x)=17,解得:x=7
当x>10时,x+4+2(x-10)=17,解得:x=11,
综上所述,答案为:7或11.
例10. 【2020·浙江苍南期末】如图,点A,P,Q,B在一条不完整的数轴上,点A表示数-3,点B表示数3,若动点P从点A出发以每秒1个单位长度向终点B匀速运动,同时动点Q从点B出发以每秒2个单位长度向终点A匀速运动,其中一点到达终点时,另一个点也随之停止运动,当BP=3AQ时,点P在数轴上表示的数是
【答案】.
【解析】解:由题意知,两点运动时间为6÷2=3秒
设运动时间为t秒,则P点表示的数为-3+t,Q点表示的数为3-2t,
BP=3-(-3+t)=6-t,AQ=3-2t-(-3)=6-2t,
∴6-t=3(6-2t),解得:t=
此时P点表示的数为-3+t=,
故答案为:.
考点五:说理
例11.【2019·北京市月考】阅读材料: 在数轴上,点 A 在原点 0 的左边,距离原点 4 个单位长度,点 B 在原点的右边,点 A 和点 B 之间的距离为 14个单位长度.
(1)点 A 表示的数是 ,点 B 表示的数是 ;
(2)点 A、B 同时出发沿数轴向左移动,速度分别为 1 个单位长度/秒,3 个单位长度/秒,经过多少秒,点 A 与点 B重合?
(3)点 M、N 分别从点 A、B 出发沿数轴向右移动,速度分别为 1 个单位长度/秒、2 个单位长度/秒,点 P 为 ON 的中点,设 OP-AM 的值为 y,在移动过程中,y 值是否发生变化?若不变,求出 y 值;若变化,说明理由.
【答案】见解析.
【解析】解:(1)由题意知,A表示的数为-4,B表示的数为10.
(2)由题意知经过(10+4)÷(3-1)=7秒,点A与点B重合.
(3)设运动时间为t 秒,
则M点表示的数为-4+t,N点表示的数为10+2t,
∵P为ON中点,
∴P点表示数为=5+t,AM=t,
∴y= OP-AM=5+t-t=5
故y值不会发生变化,y=5.
例12. 【2020·甘肃兰州期中】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合,研究数轴我们发现了许多重要的规律:数轴上点、点表示的数为、,则,两点之间的距离,若,则可简化为;线段的中点表示的数为.
(问题情境)
已知数轴上有,两点,分别表示的数为,8,点以每秒3个单位的速度沿数轴向右匀速运动,点以每秒2个单位向左匀速运动,设运动时间为秒().
(综合运用)
(1)运动开始前,,两点的距离为______;线段的中点所表示的数______.
(2)点运动秒后所在位置的点表示的数为______;点运动秒后所在位置的点表示的数为______;(用含的式子表示)
(3)它们按上述方式运动,,两点经过多少秒会相距4个单位长度?
(4)若,按上述方式继续运动下去,线段的中点能否与原点重合?若能,求出运动时间,并直接写出中点的运动方向和运动速度;若不能,请说明理由.(当,两点重合,则中点也与,两点重合).
【答案】(1)18,-1;(2)-10+3t;8-2t;(3)(4)见解析.
【解析】解:(1)AB=18,线段AB中点M表示的数为:-1.
(2)答案为:-10+3t;8-2t;
(3)设A、B两点经过t秒会相距4个单位长度,
当点A在点B左侧时,3t+2t=18-4,解得t=2.8;
当点A在点B右侧时,3t+2t=18+4,解得t=4.4,
即两点经过2.8秒或4.4秒会相距4个单位长度.
(4)能.
设A、B按上述方式继续运动k秒线段的中点M能与原点重合,
得,解得k=2,
运动开始前M点的位置是-1,运动2秒后到达原点,
由此得M点的运动方向向右,其速度为:个单位长度/秒.
考点六:综合题型
例13.如图,在数轴上,点,分别表示,9,点、分别从点、同时开始沿数轴正方向运动,点的速度是每秒3个单位,点的速度是每秒1个单位,运动时间为秒,在运动过程中,当点,点和原点这三点中的一点恰好是另外两点为端点的线段的中点时,求满足条件整数的值.
【答案】见解析.
【解析】解:当运动时间为t秒时,点P表示的数为3t-15,点Q表示的数为t+9.
当点O为线段PQ的中点时,3t-15+t+9=0,
解得:t=;
当点P为线段OQ的中点时,0+t+9=2(3t-15),
解得:t=;
当点Q为线段QP的中点时,0+3t-15=2(t+9),
解得:t=33.
综上所述:当运动时间为秒、秒或33秒时,点P,点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点.
∴整数t的值为33.
例14.【2020·永嘉县期中】已知数轴上三点,,对应的数分别为,0,3,点为数轴上任意一点,其对应的数为.
(1)如果点到点、点的距离相等,那么的值是______.
(2)数轴上是否存在点,使点到点、点的距离之和是8?若存在,求出的值;若不存在,请说明理由.
(3)如果点以每分钟1个单位长度的速度从点向右运动,同时另一点从点以每分钟2个单位长度的速度向左运动.设分钟时点和点到点的距离相等,则的值为______.(直接写出答案)
【答案】见解析.
【解析】解:(1)由题意得:3-x=x-(-1),
解得:x=1
(2)存在,∵MN=3-(-1)=4,
∴点P不可能在M、N之间.
当点P在点M的左侧时,(-1-x)+(3-x)=8,解得:x=-3;
当点P在点N的右侧时,x-(-1)+(x-3)=8,解得:x=5;
∴x=-3或x=5;
(3)当点P和点Q相遇时,t+2t=3,解得:t=1;
当点Q运动到点M的左侧时,t+1=2t-4,解得t=5;
∴t=1或t=5.
例15. (2020·甘肃兰州·七年级期中)已知:如图,点、点为数轴上两点,点表示的数为,点表示的数为,与满足.
(1)直接写出、的值,______,______;
(2)若在点和点之间有一点,且点到点的距离与到点的距离相等,动点从出发,以1个单位/秒的速度向运动,同时另一个动点从出发,以2个单位/秒的速度向点运动.若、中有一点到达终点时,另一个点也随之停止运动,设运动时间为秒,的长为(),请用含有的式子表示;
(3)在(2)的条件下,当点到点的距离是点到点距离的2倍时,求到点与点距离相等的点所表示的数.
【答案】见解析.
【解析】解:(1)答案为:-4,8;
(2)点M表示的数为:2
①当0≤t<3时,即点Q在点M右侧,y=6-2t;
②当3<t≤6时,即点Q到达点M或在点M左侧,y=2y-6.
(3)由题意得AM=BM=6,PM=6-t
①6-t=2(6-2t)解得:t=2
此时,P表示的数为-2,Q表示的数为4.
到点P与点Q距离相等的点所表示的数为1.
②6-t=2(2t-6)解得:t=3.6
此时,P表示的数为-0.4,Q表示的数为0.8
到点P与点Q距离相等的点所表示的数为0.2.
例16.【2019·兰州天庆期末】如图,点从原点出发沿数轴向左运动,同时点从原点出发沿数轴向右运动,秒钟后,两点相距个单位长度,已知点的速度是点A的速度的倍.(速度单位:单位长度/秒)
(1)求出点、点运动的速度.
(2)若、两点从(1)中位置开始,仍以原来的速度同时沿数轴向左运动,几秒时原点恰好处在点点的正中间?
(3)若、两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点同时从点位置出发向点运动,当遇到点后,立即返回向点运动,遇到点又立即返回向点运动,如此往返,直到点追上点时,点一直以单位长度/秒的速度运动,那么点从开始运动到停止运动,行驶的路程是多少单位长度.
【答案】见解析.
【解析】解:(1)设A点速度为x单位/秒,则B点速度为(3x)单位/秒,
由题意得:4(x+3x)=16,解得:x=1
即A点速度为1单位/秒,B点速度为3单位/秒.
(2)在(1)中,A、B两点运动4秒后到达点分别为:-4,12.
设y秒后原点在A与B之间,
A点表示数为:-4-y,B点表示的数为:12-3y,
∴-4-y+12-3y=0,解得:y=2
故2秒后原点在A与B之间.
(3)由题意知,B点追上A点所需时间为16÷(3-1)=8秒,
此时C点运动路程为20×8=160个单位长度.
【技能一】数轴上两点间的距离
如图,A、B表示的数为a、b,则A与B间的距离AB=|a-b|;
当a,b的大小已知时,“大减小(右减左)”,不知大小时,“绝对值”(两数差的绝对值).
【技能二】数轴上两点间中点表示的数
如图,C是AB的中点,则C表示的数x=;
理由:
AC=BC,则x-a=b-x,
∴x=.
【技能三】数轴上点移动规律
数轴上点向右移动则数变大(增加),向左移动数变小(减小);
当数a表示的点向右移动b个单位长度后到达点表示的数为a+b;向左移动b个单位长度后到达点表示的数为a-b.
例:P从A出发,以2个单位/秒速度向右运动,t秒后达到的点表示的数为:a+2t.
数轴是数形结合的产物,分析数轴上点的运动要结合图形进行分析,点在数轴上运动形成的路径可看作数轴上线段的和差关系.
考点一:求动点速度
例1.【2020·龙城期中】已知多项式的常数项是a,次数是b,且a,b两个数轴上所对应的点分别为A、B,若点A、点B同时沿数轴向正方向运动,点A的速度是点B的2倍,且3秒后,,点B的速度为 .
【答案】或.
【解析】解:由题意知a=-4,b=3,
设B点速度为x单位/秒,则A的速度为(2x)单位/秒,
3秒后,A点表示点为-4+3×2x=-4+6x,B点表示的数为3+3x,
∴OA=|-4+6x|,OB=3+3x,
∴|-4+6x|=3+3x,
解得:x=或x=
故答案为:或.
考点二:求动点运动时间
例2.【2020·江苏期中】我们知道:在数轴上,点M表示实数为a,点N表示实数为b,当 时,点M、N之间的距离记作:MN =;当时,点M、N之间的距离记作:MN =a-b,例如:, 则MN =.
如图,点A、B、C是数轴上从左向右依次排列的三点,且,,点B表示的数是.
(1)点A表示的数是 ,点C表示的数是 ;
(2)动点M、N分别从A、C同时出发,点M沿数轴向右运动,速度为1个单位长度∕秒,点N沿数轴向左运动,速度为2个单位长度∕秒,运动t秒后:
①点M表示的数 ,点N表示的数 ;(用含t的代数式表示)
②求当t为何值时,点M、N、B三点中相邻两个点之间的距离相等.(M、N、B三点中任意两点不重合).
【答案】(1)-10, 5;(2)①-10+t,5-2t;②见解析.
【解析】解:(1)∵AC=15,BC=9,
∴AB=6,
∴点A表示的数为-4-6=-10,点C表示的数为-10+15=5.
故答案为:点A表示的数为-10,点C表示的数为5.
(2)设运动时间为t时,
①AM=t,点M表示的数为-10+t;CN=2t,点N表示的数为5-2t,
②分三种情况讨论:
当B为中点时,(-10+t)+(5-2t)=2×(-4),解得t=3;
当N为中点时,(-10+t)+(-4)=2×(5-2t),解得t=4.8;
当M为中点时,(5-2t) +(-4)=2×(-10+t),解得t=5.25;
综上所述,当t为3秒或4.8秒或5.25秒时,点M,N,B三点中相邻两个点之间的距离相等.
例3. 【2020·杭州月考】已知数轴上两点A、B对应的数分别为-1,3,点P为数轴上一动点,其对应的数为x.
(1)若点到点、点的距离相等,则点对应的数为______.
(2)利用数轴探究:找出满足的的所有值是______.
(3)当点以每秒6个单位长的速度从点向右运动时,点以每秒6个单位长的速度向右运动,点以每秒钟5个单位长的速度向右运动,问它们同时出发,几秒后点到点、点的距离相等?
【答案】(1)1;(2)-3或5;(3)2秒或4秒.
【解析】解:(1)∵点P到点A、点B的距离相等
∴x+1=3-x,解得x=1,
即点P表示的数为1.
(2)①当x>3时,
x-3+x+1=8,解得:x=5.
②当x<-1时,
3-x-x-1=8,解得:x=-3.
③当-1≤x≤3时,|x-3|+|x+1|=4≠8,不成立,
∴满足原方程的所有值为:-3或5;
故答案为:-3或-5.
(3)分两种情况:
①当P点在AB之间时.则5x+3-6x=1.解得:x=2
②当P点在AB右侧时,此时A、B重合
则5x+4=6x.解得:x=4
综上所述:它们同时出发,2秒或4秒后P到点A、点B的距离相等.
例4. 【2020·云南官渡期中】如图,数轴上的点和点分别表示0和10,点是线段上一动点.点沿以每秒2个单位的速度往返运动1次,是线段的中点,设点运动时间为秒(不超过10秒).若点在运动过程中,当时,则运动时间的值为
【答案】或或或.
【解析】解:由题意知,B点表示的数为5,
当PB=2时,P点表示的数为3或7,
(1)当P从O到A运动时,PB=2时,则t=或;
(2)当P从A到O运动时,PB=2时,则t=或;
故答案为:或或或.
例5. 【2020·湖北孝感月考】已知数轴上有、两个点对应的数分别是、,且满足;
(1)求、的值;
(2)点是数轴上、之间的一个点,使得,求出点所对应的数;
(3)点,点为数轴上的两个动点,点从点以3个单位长度每秒的速度向右运动,点同时从点以2个单位长度每秒的速度向左运动,设运动时间为秒,若,求时间的值.
【答案】见解析.
【解析】解:(1)∵,
∴a+3=0,b-9=0,
∴a=-3,b=9.
(2)设M点表示的数为x,
∵AM=2BM,
∴x+3=2(9-x)
解得:x=5
即M点表示的数为5.
(3)由题意知,AP=3t,BQ=2t,P点表示的数为3t-3,Q点表示的数为9-2t,
∴PQ=|9-2t-3t+3|=|12-5t|,
∴3t+2t=2|12-5t|,
解得:t=或t=
综上所述,t=或t=时,满足题意.
例6. 【2020·东安实验学校期中】数轴上点A表示的有理数为20,点B表示的有理数为-10,点P从点A出发以每秒5个单位长度的速度在数轴上往左运动,到达点B后立即返回,返回过程中的速度是每秒2个单位长度,运动至点A停止,设运动时间为t(单位:秒).
(1)当t=5时,点P表示的有理数为 .
(2)在点P往左运动的过程中,点P表示的有理数为 (用含t的代数式表示).
(3)当点P与原点距离5个单位长度时,t的值为 .
【答案】(1)-5;(2)20-5t;(3)3;5;8.5;13.5.
【解析】解:(1)由题意得:AB=30,
点P从点A运动到点B所需时间为:30÷5=6秒,
点P从点B返回,运动到点A所需时间为30÷2=15秒,
则当t=5时,PA=25,
∴点P表示的有理数为20-25=-5,
故答案为:-5;
(2)在点P往左运动的过程中,PA=5t,
则点P表示的有理数为20-5t,
故答案为:20-5t;
(3)①当点P从点A运动到点B时,
由(2)可知,,
解得t=3或t=5;
②当点P从点B返回,运动到点A,
由题意知P点表示的数为2(t-6)-10=2t-22,
则,
解得t=8.5或t=13.5
故答案为:3或5或8.5或13.5.
考点三:新定义类型
例7. 阅读理解:若为数轴上三点,若点到的距离是点到的距离2倍,我们就称点是的好点.例如,如图1,点是的好点:点是的好点.
(1)如图2,为数轴上两点,点所表示的数为,点所表示的数为4.在数轴上的好点所表示的数是__________.
(2)如图3,为数轴上两点,点所表示的数为,点所表示的数为40.现有一只电子蚂蚁从点出发,以2个单位每秒的速度向左运动,到达点停止.当为何值时,P、A和中恰有一个点为其余两点的好点?
【答案】(1)0;(2)见解析.
【解析】解:(1)设所求的数为x,根据题意得:
4-x=2(x+2),解得:x=0,
故答案为:0.
(2)设点P表示的数为y,
①当点P为【A,B】的好点,由题意得:
y+20=2(40-y),解得:y=20,
∴t=10 秒;
②当P为【B,A】的好点,由题意得:
40-y=2(y+20),解得y=0,
∴t=20秒
③当B为【A,P】的好点,由题意得:
40+20=2(40-y),解得:y=10,
∴t=(40-10)÷2=15秒;
④当A为【B,P】的好点,由题意得:
40+20=2(y+20),解得:y=10,
∴t=(40-10)÷2=15秒;
综上所述:当t的值为10或15或20时,P、A和B中恰有一个点为其余两点的好点.
例8. 【2019·广州市期中】数轴上有三点,给出如下定义;若其中一个点与其他两个点的距离恰好满足倍的数量关系,则称该点是其它两个点的:“关联点”
(1)例图,数轴上点三点所表示的数分别为,点到点的距离 ,点到点的距离是 ,因为是的两倍,所以称点是点的“关联点”.
(2)若点表示数点表示数,下列各数所对应的点分别是,其中是点的“关联点”的是 ;
(3)点表示数,点表示数为数轴上一个动点;若点在点的左侧,且点是点的“关联点”,求此时点表示的数;若点在点的右侧,点中,有一个点恰好是其它两个点的“关联点”.请直接写出此时点表示的数.
【答案】(1)2,1;(2)C1,C3(3)见解析.
【解析】解:(1)由题意知,AB=3-1=2,BC=4-3=1
故答案是:2,1;
(2)点A表示的数为-2,点B表示的数为1,C1表示的数为-1,
∴AC1=1,BC1=2,
∴C1是点A、B的“关联点”;
同理,C2、C4不是点A、B的“关联点”,C3是点A、B的“关联点”.
故答案为:C1,C3.
(3)①若点P在点B的左侧,且点P是点A,B的“关联点”,设点P表示的数为x
(I) 当P在点A的左侧时,则有:2PA=PB,即2(-10-x)=15-x
解得:x=-35
(II)当点P在A,B之间时,有2PA=PB或PA=2PB
有2(x+10)=15-x或x+10=2(15-x)
解得:x=或x=
∴点P表示的数为-35或或.
②若点P在点B的右侧
(I)若点P是A,B的“关联点”则有2PB=PA
即2(x-15)=x+10
解得:x=40
(II)若点B是A,P的“关联点”则有2AB=PB或AB=2PB
即2(15+10)=x-15或15+10=2(x-15)
解得x=65或x=
(III)若点A是B,P的“关联点”则有2AB=AP
即2(15+10)=x+10
解得x=40
∴点P表示的数为40或65或.
考点四:求动点表示的数
例9.【河北期末】如图,点为数轴的原点,点对应的数为,点对应的数为,且,点为数轴上的动点,且点对应的数为.当时,的值为 .
【答案】7或11.
【解析】解:由题意知,a=-4,b=10,
当x<-4时,PA=-4-x,PB=10-x,
∴-4-x+2(10-x)=17,解得:x=(舍)
当-4≤x≤10时,x+4+2(10-x)=17,解得:x=7
当x>10时,x+4+2(x-10)=17,解得:x=11,
综上所述,答案为:7或11.
例10. 【2020·浙江苍南期末】如图,点A,P,Q,B在一条不完整的数轴上,点A表示数-3,点B表示数3,若动点P从点A出发以每秒1个单位长度向终点B匀速运动,同时动点Q从点B出发以每秒2个单位长度向终点A匀速运动,其中一点到达终点时,另一个点也随之停止运动,当BP=3AQ时,点P在数轴上表示的数是
【答案】.
【解析】解:由题意知,两点运动时间为6÷2=3秒
设运动时间为t秒,则P点表示的数为-3+t,Q点表示的数为3-2t,
BP=3-(-3+t)=6-t,AQ=3-2t-(-3)=6-2t,
∴6-t=3(6-2t),解得:t=
此时P点表示的数为-3+t=,
故答案为:.
考点五:说理
例11.【2019·北京市月考】阅读材料: 在数轴上,点 A 在原点 0 的左边,距离原点 4 个单位长度,点 B 在原点的右边,点 A 和点 B 之间的距离为 14个单位长度.
(1)点 A 表示的数是 ,点 B 表示的数是 ;
(2)点 A、B 同时出发沿数轴向左移动,速度分别为 1 个单位长度/秒,3 个单位长度/秒,经过多少秒,点 A 与点 B重合?
(3)点 M、N 分别从点 A、B 出发沿数轴向右移动,速度分别为 1 个单位长度/秒、2 个单位长度/秒,点 P 为 ON 的中点,设 OP-AM 的值为 y,在移动过程中,y 值是否发生变化?若不变,求出 y 值;若变化,说明理由.
【答案】见解析.
【解析】解:(1)由题意知,A表示的数为-4,B表示的数为10.
(2)由题意知经过(10+4)÷(3-1)=7秒,点A与点B重合.
(3)设运动时间为t 秒,
则M点表示的数为-4+t,N点表示的数为10+2t,
∵P为ON中点,
∴P点表示数为=5+t,AM=t,
∴y= OP-AM=5+t-t=5
故y值不会发生变化,y=5.
例12. 【2020·甘肃兰州期中】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合,研究数轴我们发现了许多重要的规律:数轴上点、点表示的数为、,则,两点之间的距离,若,则可简化为;线段的中点表示的数为.
(问题情境)
已知数轴上有,两点,分别表示的数为,8,点以每秒3个单位的速度沿数轴向右匀速运动,点以每秒2个单位向左匀速运动,设运动时间为秒().
(综合运用)
(1)运动开始前,,两点的距离为______;线段的中点所表示的数______.
(2)点运动秒后所在位置的点表示的数为______;点运动秒后所在位置的点表示的数为______;(用含的式子表示)
(3)它们按上述方式运动,,两点经过多少秒会相距4个单位长度?
(4)若,按上述方式继续运动下去,线段的中点能否与原点重合?若能,求出运动时间,并直接写出中点的运动方向和运动速度;若不能,请说明理由.(当,两点重合,则中点也与,两点重合).
【答案】(1)18,-1;(2)-10+3t;8-2t;(3)(4)见解析.
【解析】解:(1)AB=18,线段AB中点M表示的数为:-1.
(2)答案为:-10+3t;8-2t;
(3)设A、B两点经过t秒会相距4个单位长度,
当点A在点B左侧时,3t+2t=18-4,解得t=2.8;
当点A在点B右侧时,3t+2t=18+4,解得t=4.4,
即两点经过2.8秒或4.4秒会相距4个单位长度.
(4)能.
设A、B按上述方式继续运动k秒线段的中点M能与原点重合,
得,解得k=2,
运动开始前M点的位置是-1,运动2秒后到达原点,
由此得M点的运动方向向右,其速度为:个单位长度/秒.
考点六:综合题型
例13.如图,在数轴上,点,分别表示,9,点、分别从点、同时开始沿数轴正方向运动,点的速度是每秒3个单位,点的速度是每秒1个单位,运动时间为秒,在运动过程中,当点,点和原点这三点中的一点恰好是另外两点为端点的线段的中点时,求满足条件整数的值.
【答案】见解析.
【解析】解:当运动时间为t秒时,点P表示的数为3t-15,点Q表示的数为t+9.
当点O为线段PQ的中点时,3t-15+t+9=0,
解得:t=;
当点P为线段OQ的中点时,0+t+9=2(3t-15),
解得:t=;
当点Q为线段QP的中点时,0+3t-15=2(t+9),
解得:t=33.
综上所述:当运动时间为秒、秒或33秒时,点P,点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点.
∴整数t的值为33.
例14.【2020·永嘉县期中】已知数轴上三点,,对应的数分别为,0,3,点为数轴上任意一点,其对应的数为.
(1)如果点到点、点的距离相等,那么的值是______.
(2)数轴上是否存在点,使点到点、点的距离之和是8?若存在,求出的值;若不存在,请说明理由.
(3)如果点以每分钟1个单位长度的速度从点向右运动,同时另一点从点以每分钟2个单位长度的速度向左运动.设分钟时点和点到点的距离相等,则的值为______.(直接写出答案)
【答案】见解析.
【解析】解:(1)由题意得:3-x=x-(-1),
解得:x=1
(2)存在,∵MN=3-(-1)=4,
∴点P不可能在M、N之间.
当点P在点M的左侧时,(-1-x)+(3-x)=8,解得:x=-3;
当点P在点N的右侧时,x-(-1)+(x-3)=8,解得:x=5;
∴x=-3或x=5;
(3)当点P和点Q相遇时,t+2t=3,解得:t=1;
当点Q运动到点M的左侧时,t+1=2t-4,解得t=5;
∴t=1或t=5.
例15. (2020·甘肃兰州·七年级期中)已知:如图,点、点为数轴上两点,点表示的数为,点表示的数为,与满足.
(1)直接写出、的值,______,______;
(2)若在点和点之间有一点,且点到点的距离与到点的距离相等,动点从出发,以1个单位/秒的速度向运动,同时另一个动点从出发,以2个单位/秒的速度向点运动.若、中有一点到达终点时,另一个点也随之停止运动,设运动时间为秒,的长为(),请用含有的式子表示;
(3)在(2)的条件下,当点到点的距离是点到点距离的2倍时,求到点与点距离相等的点所表示的数.
【答案】见解析.
【解析】解:(1)答案为:-4,8;
(2)点M表示的数为:2
①当0≤t<3时,即点Q在点M右侧,y=6-2t;
②当3<t≤6时,即点Q到达点M或在点M左侧,y=2y-6.
(3)由题意得AM=BM=6,PM=6-t
①6-t=2(6-2t)解得:t=2
此时,P表示的数为-2,Q表示的数为4.
到点P与点Q距离相等的点所表示的数为1.
②6-t=2(2t-6)解得:t=3.6
此时,P表示的数为-0.4,Q表示的数为0.8
到点P与点Q距离相等的点所表示的数为0.2.
例16.【2019·兰州天庆期末】如图,点从原点出发沿数轴向左运动,同时点从原点出发沿数轴向右运动,秒钟后,两点相距个单位长度,已知点的速度是点A的速度的倍.(速度单位:单位长度/秒)
(1)求出点、点运动的速度.
(2)若、两点从(1)中位置开始,仍以原来的速度同时沿数轴向左运动,几秒时原点恰好处在点点的正中间?
(3)若、两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点同时从点位置出发向点运动,当遇到点后,立即返回向点运动,遇到点又立即返回向点运动,如此往返,直到点追上点时,点一直以单位长度/秒的速度运动,那么点从开始运动到停止运动,行驶的路程是多少单位长度.
【答案】见解析.
【解析】解:(1)设A点速度为x单位/秒,则B点速度为(3x)单位/秒,
由题意得:4(x+3x)=16,解得:x=1
即A点速度为1单位/秒,B点速度为3单位/秒.
(2)在(1)中,A、B两点运动4秒后到达点分别为:-4,12.
设y秒后原点在A与B之间,
A点表示数为:-4-y,B点表示的数为:12-3y,
∴-4-y+12-3y=0,解得:y=2
故2秒后原点在A与B之间.
(3)由题意知,B点追上A点所需时间为16÷(3-1)=8秒,
此时C点运动路程为20×8=160个单位长度.
相关资料
更多








