



专题02 化动为静,破解几何动态问题 2022年七年级数学寒假辅导讲义(人教版)
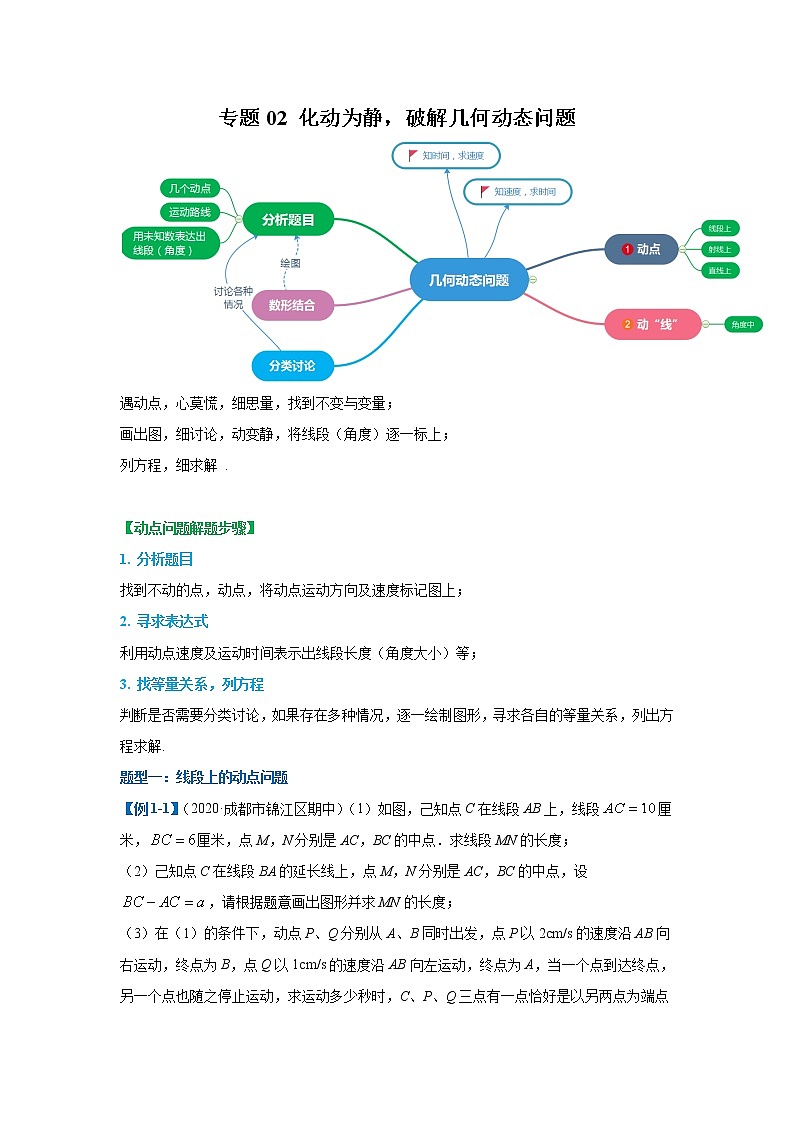
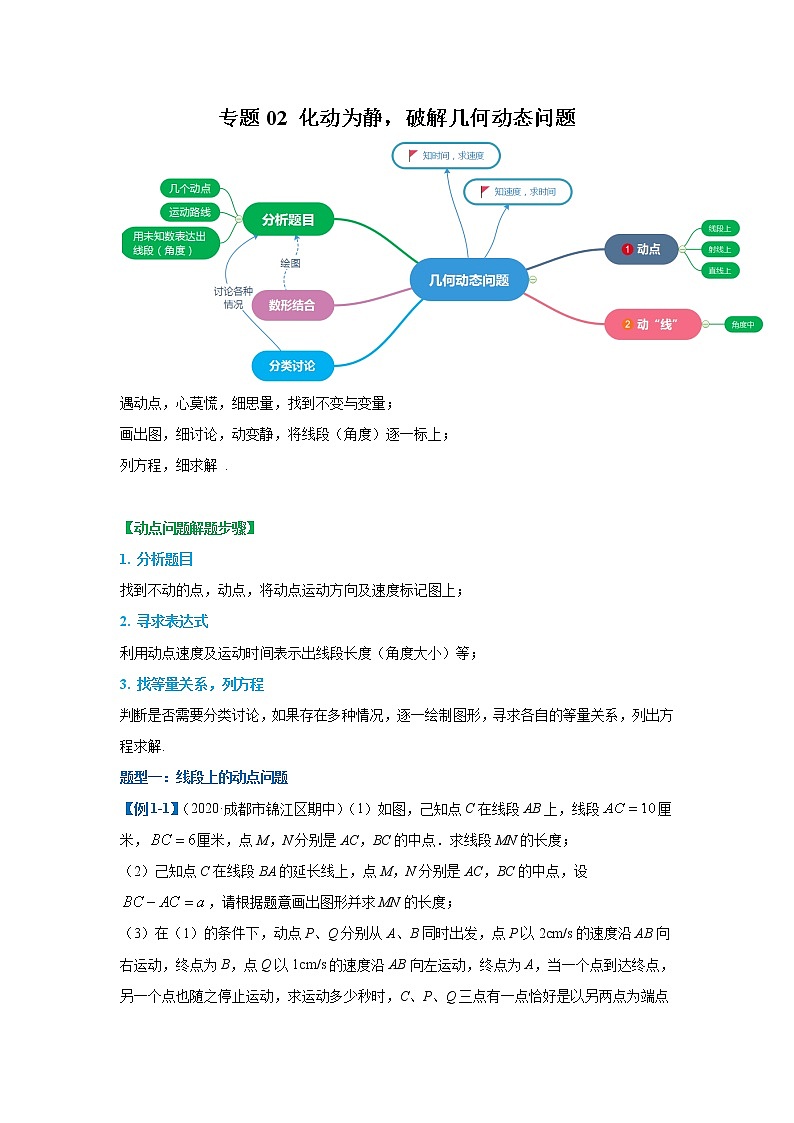
展开专题02 化动为静,破解几何动态问题
遇动点,心莫慌,细思量,找到不变与变量;
画出图,细讨论,动变静,将线段(角度)逐一标上;
列方程,细求解 .
【动点问题解题步骤】
1. 分析题目
找到不动的点,动点,将动点运动方向及速度标记图上;
2. 寻求表达式
利用动点速度及运动时间表示出线段长度(角度大小)等;
3. 找等量关系,列方程
判断是否需要分类讨论,如果存在多种情况,逐一绘制图形,寻求各自的等量关系,列出方程求解.
题型一:线段上的动点问题
【例1-1】(2020·成都市锦江区期中)(1)如图,己知点C在线段AB上,线段厘米,厘米,点M,N分别是AC,BC的中点.求线段MN的长度;
(2)己知点C在线段BA的延长线上,点M,N分别是AC,BC的中点,设,请根据题意画出图形并求MN的长度;
(3)在(1)的条件下,动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点.
【例1-2】(2020·丹东市期中)如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若,求线段MN的长;
(2)若C为线段AB上一动点,满足,其它条件不变,你能猜想MN的长度吗?你能用一句简洁的话描述你发现的结论吗?
【变式1-1】(2020·江西南昌市期末)已知:如图1,点M是线段AB上一定点,AB=12cm,C、D两点分别从M、B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AM=4cm,当点C、D运动了2s,此时AC= ,DM= ;(直接填空)
(2)当点C、D运动了2s,求AC+MD的值.
(3)若点C、D运动时,总有MD=2AC,则AM= (填空)
(4)在(3)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.
【变式1-2】(2020·河南南阳市期中)如图一,点在线段上,图中有三条线段、和,若其中一条线段的长度是另外一条线段长度的倍,则称点是线段的“巧点”.
(1)填空:线段的中点 这条线段的巧点(填“是”或“不是”或“不确定是”)
(问题解决)
(2)如图二,点和在数轴上表示的数分别是和,点是线段的巧点,求点在数轴上表示的数.
(应用拓展)
(3)在(2)的条件下,动点从点处,以每秒个单位的速度沿向点匀速运动,同时动点从点出发,以每秒个单位的速度沿向点匀速运动,当其中一点到达终点时,两个点运动同时停止,当、、三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间的所有可能值.
题型二:折线上的动点问题
【例2-1】(2020·镇江市月考)如图,将一条数轴在原点和点处各折一下,得到一条“折线数轴”.图中点表示,点表示10,点表示18,我们称点和点在数轴上相距28个长度单位.动点、同时出发,点从点出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点运动到点期间速度变为原来的一半,之后立刻恢复原速;动点从点出发,以1单位/秒的速度沿着数轴的负方向运动,从点运动到点期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为秒.问:
(1)动点从点运动至点需要多少时间?
(2)、两点相遇时,求出相遇点所对应的数是多少;
(3)求当为何值时,、两点在数轴上相距的长度与、两点在数轴上相距的长度相等.
【变式2-1】(2020·浙江模拟)如图,数轴上,点A表示的数为,点B表示的数为,点C表示的数为9,点D表示的数为13,在点B和点C处各折一下,得到条“折线数轴”,我们称点A和点D在数上相距20个长度单位,动点P从点A出发,沿着“折线数轴”的正方向运动,同时,动点Q从点D出发,沿着“折线数轴”的负方向运动,它们在“水平路线”射线和射线上的运动速度相同均为2个单位/秒,“上坡路段”从B到C速度变为“水平路线”速度的一半,“下坡路段”从C到B速度变为“水平路线”速度的2倍.设运动的时间为t秒,问:
(1)动点P从点A运动至D点需要时间为________秒;
(2)P、Q两点到原点O的距离相同时,求出动点P在数轴上所对应的数;
(3)当Q点到达终点A后,立即调头加速去追P,“水平路线”和“上坡路段”的速度均提高了1个单位/秒,当点Q追上点P时,直接写出它们在数轴上对应的数.
【变式2-2】(2019·武汉月考)如图1,在数轴上有一条线段AB,,表示的数分别是-2和-7.
(1)若将线段AB的一端平移到原点处,则平移的距离为 ;
(2)如图2,C为线段AB上一点,以点C为折点,将此数轴向右对折,若点落在点的左边且,求C点对应的数;
(3)移动线段AB,使A对应的数为15,则B对应的数为 (直接填空),此时数轴上的动点M,N分别从A,B出发向左作匀速运动,速度分别为4单位长度/秒和2单位长度/秒,请问数轴上是否存在定点P,当动点M在线段OA上移动过程中始终满足OM=2PN,若存在求点P对应的数;若不存在,请说明理由.
题型三:角度中的动点问题
【例3-1】(2020·江苏盐城市月考)七年级学生小聪和小明完成了数学实验《钟面上的数学》后,制作了一个模拟钟面,如图所示,点O为模拟钟面的圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA顺时针转动,OB逆时针转动,OA运动速度为每秒转动15°,OB运动速度为每秒转动5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒(t>0),请你试着解决他们提出的下列问题:
(1)OA顺时针转动,OB逆时针转动,当t= 秒时,OA与OB第一次重合;
(2)OA顺时针转动,OB逆时针转动,当t=3秒时,∠AOB= °;
(3)若他们同时顺时针转动,t为何值时,OA与OB的夹角为20°?
(4)若他们同时顺时针转动,t为何值时,ON平分OA与OB的夹角?OA平分OB与ON的夹角?
【变式3-1】(2020·焦作市月考)已知数轴有A、B两点,分别表示的数为a、b,且|a+12|+|b﹣18|=0.
(1)a= ,b= ,点A和点B之间的距离为 ;
(2)如图1,动点P沿线段AB自点A向点B以2个单位长度/秒的速度运动,同时动点Q沿线段BA自点B向点A以4个单位/秒的速度运动,经过 秒,动点P,Q两点能相遇;
(3)如图1,点P沿线段AB自点A向点B以2个单位/秒的速度运动,点P出发3秒后,点Q沿线段BA自点B向A以4个单位/秒的速度运动,问再经过几秒P,Q两点相距6个单位长度;
(4)如图2,AO=4厘米,PO=2厘米,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自点B向点A运动,假若点P,Q两点能相遇,直接写出点Q运动的速度.
【变式3-2】(浙江月考)已知:如图1,点A、O、B依次在度线MN上,现将射线OA绕点O沿顺时针方向以每秒3°的速度旋转,同时射线OB绕点O沿进时针方向以每秒6°的速度前转,如图2,设旋转时间为t(0秒≤t≤60秒).
(1)用含的代数式表示下列各角的度数:______,______.
(2)在运动过程中,当0秒秒时,=45°,求t的值.
(3)在旋转过程中是否存在这样的,使得射线是由射线.射线、射线中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出的值;如果不存在,请说明理由.








