初中数学人教版八年级下册17.2 勾股定理的逆定理教学ppt课件

这是一份初中数学人教版八年级下册17.2 勾股定理的逆定理教学ppt课件，共14页。PPT课件主要包含了勾股定理的逆命题，应用新知，∠A900，谁与争锋等内容，欢迎下载使用。
1、什么是命题的题设和结论？（回忆）
3、什么是互为逆定理？
两个命题中, 如果它们的题设、结论正好相反,那么这两个命题叫做互逆命题.
如果把其中一个叫做原命题, 那么另一个叫做它的逆命题.
题设是已知事项，结论是题设推出的结果。
一般，如果后面是题设，那么后面是结论。
如果一个定理的逆命题经过证明是正确的, 那么它也是一个定理, 称这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.
古埃及人曾用下面的方法得到直角
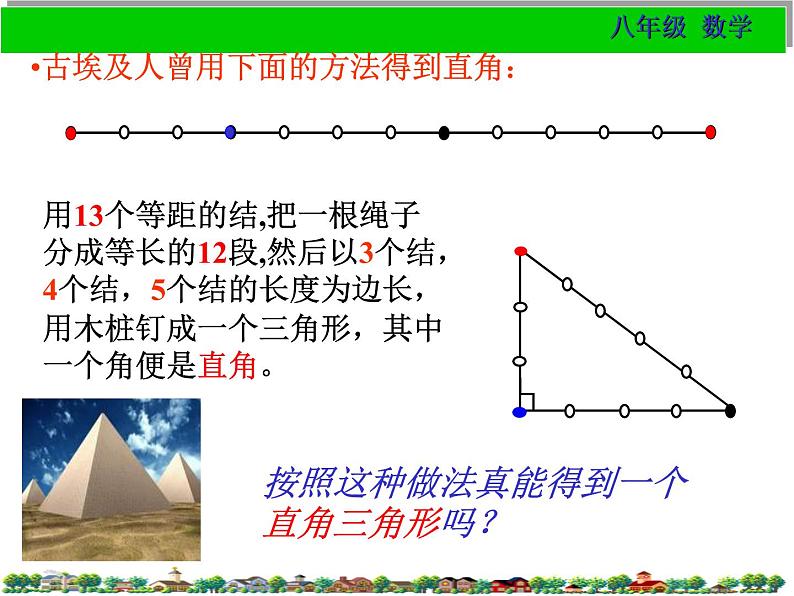
按照这种做法真能得到一个直角三角形吗？
古埃及人曾用下面的方法得到直角：
用13个等距的结,把一根绳子分成等长的12段,然后以3个结，4个结，5个结的长度为边长，用木桩钉成一个三角形，其中一个角便是直角。
　　勾股定理　如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2=c2．
　　题设（条件）：直角三角形的两直角边长为a，b，斜边长为c ．
　　结论：a2+b2=c2．
回忆旧知　再次梳理
如果三角形的三边长a，b，c ，且满足a2+b2=c2，那么这个三角形是直角三角形。
∴ A′B′2= a2+b2
∴ A′B′ 2=c2
∴ △ ABC ≌△ A′B′C′（SSS）
∴ ∠ C= ∠ C′ (全等三角形 对应角相等）
已知:在△ABC中，AB=c ， BC=a ，CA=b， 且a2+b2=c2
求证:△ ABC是直角三角形
证明:画一个△A′B′C′,使∠ C′=900,B′C′=a, C′A′=b
在△ ABC和△ A′B′C′中
∴ △ ABC是直角三角形（直角三角形的定义）
如果三角形的三边长a，b，c 满足a2+b2=c2，那么这个三角形是直角三角形。
(1)两条直线平行，内错角相等．(2)如果两个实数相等，那么它们的平方相等．(3)如果两个实数相等，那么它们的绝对值相等．(4)全等三角形的对应角相等．
说出下列命题的逆命题．这些命题的逆命题成立吗?
逆命题: 内错角相等，两条直线平行. 成立
逆命题:如果两个实数的平方相等，那么这两个实数相等. 不成立
逆命题:如果两个实数的绝对值相等，那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
判断由a、b、c组成的三角形是不是直角三角形：(1) a＝15 , b ＝8 , c＝17
(2) a＝13 , b ＝15 , c＝14
（1）解：∵152＋82＝225＋64＝289 172＝289 ∴ 152＋82＝172 ∴这个三角形是直角三角形
运用勾股定理的关键是较小两数的平方和等于最大数的平方。
下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数，称为勾股数.
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形