第2讲 函数小题 2022高考新题好题汇编

第2讲 函数小题

一、单选题

1．（2021·全国高三专题练习（文））已知，，，则（    ）

A． B．

C． D．

【答案】D

【分析】

先证明，再证明，即得解.

【详解】

，

，

因为，

所以.

故选：D

【点睛】

关键点睛：解答本题的关键在于熟练掌握指数对数函数的运算和性质，从而达到比较大小的目的.

2．（2021·广东汕头市·高三一模）若，则（    ）

A． B．1 C． D．3

【答案】B

【分析】

根据指对数的关系得，代入目标式求值即可.

【详解】

由题意知：，即.

故选：B.

3．（2021·广东广州市·高三一模）2020年11月10日，我国“奋斗者”号载人深潜器在马里亚纳海沟成功坐底，下潜深度达到惊人的，创造了我国载人深潜的新记录.当“奋斗者”号下潜至某一深度时，处于其正上方海面处的科考船用声呐装置向“奋斗者”号发射声波.已知声波在海水中传播的平均速度约为，若从发出至回收到声波所用时间为，则“奋斗者”号的实际下潜深度约为（    ）

A． B． C． D．

【答案】B

【分析】

可得声波从海面传到“奋斗者”号的时间为3s，即可求出实际下潜深度.

【详解】

可得声波从海面传到“奋斗者”号的时间为，

则“奋斗者”号的实际下潜深度约为.

故选：B.

4．（2021·广东湛江市·高三一模）已知a=3.20.1，b=log25，c=log32，则（    ）

A．b>a>c B．c>b>a C．b>c>a D．a>b>c

【答案】A

【分析】

由指数函数和对数函数得单调性即可得出结果.

【详解】

所以

故选：A

5．（2021·广东韶关市·高三一模）人的心脏跳动时，血压在增加或减少.血压的最大值､最小值分别称为收缩压和舒张压，血压计上的读数就是收缩压和舒张压，读数为标准值.设某人的血压满足函数式，其中为血压(单位：)，为时间(单位：)，则下列说法正确的是（    ）

A．收缩压和舒张压均高于相应的标准值 B．收缩压和舒张压均低于相应的标准值

C．收缩压高于标准值，舒张压低于标准值 D．收缩压低于标准值，舒张压高于标准值

【答案】C

【分析】

根据已知函数式求得收缩压和舒张压，与标准值比较可得．

【详解】

由三角函数知识，函数的最大值(即收缩压)为126，函数的最小值(即舒张压)为76，比较得：收缩压高与标准值，舒张压低于标准值，

故选：C.

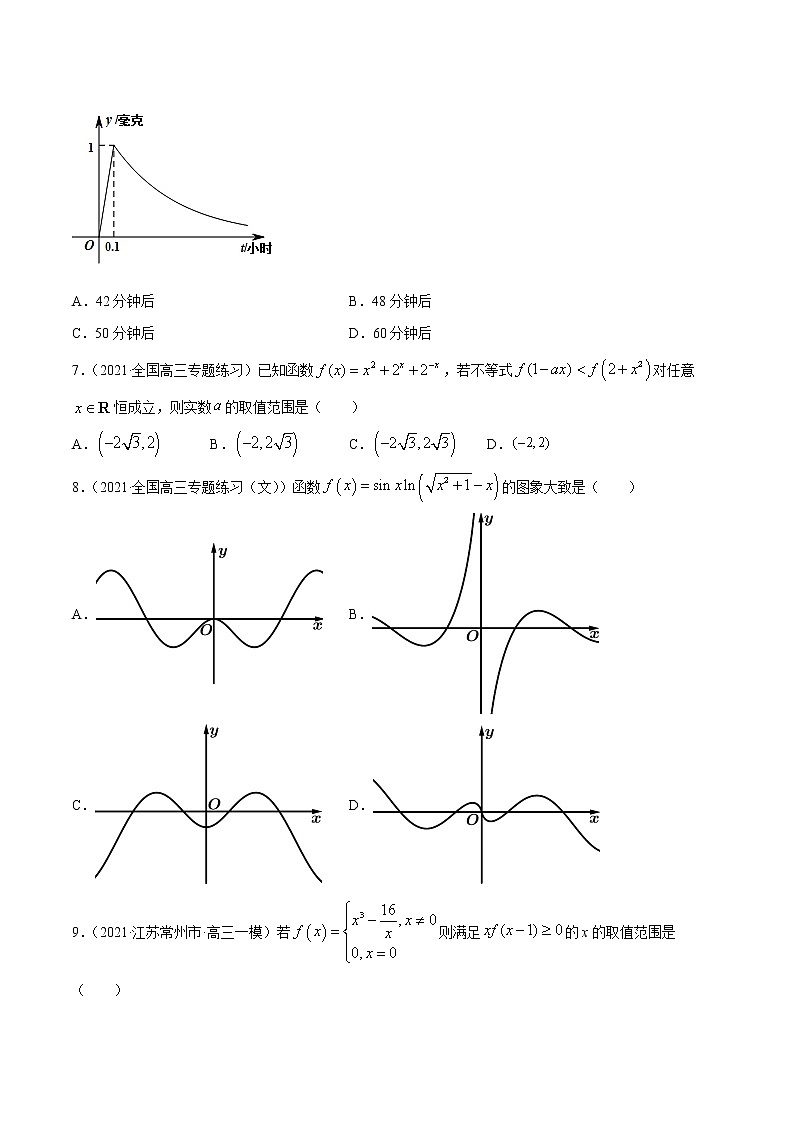
6．（2021·广东揭阳市·高三一模）在新冠肺炎疫情期间，某学校定期对教室进行药熏消毒.教室内每立方米空气中的含药量（单位：毫克）随时间（单位：小时）的变化情况如图所示.在药物释放的过程中，与成正比；药物释放完毕后，与的函数关系式为（为常数）.据测定，当空气中每立方米的含药量降低到0.2毫克以下时，学生方可进入教室.那么，从药物释放开始到学生能回到教室，至少在（    ）（参考数值）

A．42分钟后 B．48分钟后

C．50分钟后 D．60分钟后

【答案】B

【分析】

根据函数图象求出时的函数解析式，即求出的值，再解不等式求得答案.

【详解】

把点代入中，，解得.

所以当时，

因为当空气中每立方米的含药量降低到0.2毫克以下时，学生方可进入教室

所以，解得.

至少需要经过分钟后，学生才能回到教室.

故选：B.

7．（2021·全国高三专题练习）已知函数，若不等式对任意恒成立，则实数的取值范围是（    ）

A． B． C． D．

【答案】D

【分析】

先利用定义确定函数为偶函数，再利用单调性证明在上为增函数，所以不等式化简为，转化为在上恒成立，求出的取值范围.

【详解】

函数的定义域为，且，所以为偶函数.

又当时, 是增函数，

任取，且，

，，

所以在上是增函数，即在上是增函数.

所以不等式对任意恒成立，转化为，即，从而转化为和在上恒成立

①若在上恒成立，则，解得；

②若在上恒成立，，则，解得；

综上所述，实数的取值范围是.

故选：D.

【点睛】

方法点睛：本题考查了解抽象不等式，要设法把隐性划归为显性的不等式求解，方法是：

（1）把不等式转化为的模型；

（2）判断函数的单调性，再根据函数的单调性将不等式的函数符号“”脱掉，得到具体的不等式（组）来求解，但要注意奇偶函数的区别.

8．（2021·全国高三专题练习（文））函数的图象大致是（    ）

A． B．

C． D．

【答案】A

【分析】

根据，排除B、C选项；再由函数的奇偶性，排除D选项，即可求解.

【详解】

由题意，函数，可得，可排除B、C选项；

又由

，

所以函数为偶函数，所以排除D选项.

故选：A.

9．（2021·江苏常州市·高三一模）若则满足的x的取值范围是（    ）

A． B．

C． D．

【答案】B

【分析】

按或0，，和四种情况，分别化简解出不等式，可得x的取值范围．

【详解】

①当或0时，成立；

②当时，，可有，解得；

③当且时，

若，则，解得

若，则，解得

所以

则原不等式的解为，

故选：B

10．（2021·浙江高三专题练习）函数在其定义域上的图象大致为（    ）

A． B．

C． D．

【答案】D

【分析】

可判断函数为奇函数，再根据时的符号可得正确的选项.

【详解】

函数的定义域为，它关于原点对称.

又，故为奇函数，故排除AB选项，

又当时，，

故选：D.

11．（2021·辽宁沈阳市·高三一模）技术的数学原理之一是著名的香农公式:.它表示:在受噪声干扰的信道中，最大信息传递速度取决于信道带宽，信道内信号的平均功率，信道内部的高斯噪声功率的大小，其中叫做信噪比.当信噪比较大时，公式中真数中的可以忽略不计.假设目前信噪比为若不改变带宽，而将最大信息传播速度提升那么信噪比要扩大到原来的约（    ）

A．倍 B．倍 C．倍 D．倍

【答案】D

【分析】

根据题意可得，，两式联立，再利用对数函数的单调性求解.

【详解】

由条件可知，

设将最大信息传播速度提升

那么信噪比要扩大到原来的倍，

则，

所以，

即，

所以，

解得，

故答案为：D

12．（2021·全国高三专题练习）下列函数中，既是奇函数，又在上单调递减的是（    ）

A． B．

C． D．

【答案】B

【分析】

利用函数奇偶性的定义判断各选项中函数的奇偶性，利用导数法判断各选项中函数在区间上的单调性，由此可得出合适的选项.

【详解】

对于A选项，由，解得，

所以，函数的定义域为，该函数为非奇非偶函数，A选项不满足条件；

对于B选项，由，可得，即函数的定义域为.

，该函数为奇函数，

当时，，

所以，函数在上单调递减，B选项满足条件；

对于C选项，由，解得，所以，函数的定义域为，

，该函数为奇函数，

当时，，该函数在上为增函数，C选项不满足条件；

对于D选项，函数的定义域为，

，该函数为奇函数，

当时，，该函数在上为增函数，D选项不满足条件.

故选：B.

【点睛】

方法点睛：函数单调性的判定方法与策略：

（1）定义法：一般步骤：设元作差变形判断符号得出结论；

（2）图象法：如果函数是以图象的形式给出或者函数的图象易作出，结合图象可得出函数的单调区间；

（3）导数法：先求出函数的导数，利用导数值的正负确定函数的单调区间；

（4）复合函数法：先将函数分解为内层函数和外层函数，再讨论这两个函数的单调性，然后根据复合函数法“同增异减”的规则进行判定.

13．（2021·河南高三月考（文））函数的部分图象大致是（    ）

A． B．

C． D．

【答案】D

【分析】

通过函数的定义域判断选项C，通过函数的奇偶性判断选项B，当时，通过函数的正负判断选项A，即可得出结果.

【详解】

因为，

所以的定义域为，

则，故排除C；

而，

所以为奇函数，

其图象关于原点对称，故排除B；

当时，，，所以排除A．

故选：D．

14．（2021·全国高三专题练习（理））溶液酸碱度是通过计算的，的计算公式为，其中表示溶液中氢离子的浓度，单位是摩尔/升，人体血液的氢离子的浓度通常在之间，如果发生波动，就是病理现象，那么，正常人体血液的值的范围是（    ）

A． B． C． D．

【答案】D

【分析】

按题设所给公式求相应的值即可.

【详解】

依题意，，因此，正常人体血液的值的范围是．

故选:D．

15．（2020·江西九江市·九江七中高三期中（文））函数的图象大致为（   ）

A． B．

C． D．

【答案】A

【分析】

由函数为奇函数，图象关于原点对称，排除B项；又因为，排除C项；又因为，排除D项，即可得到答案.

【详解】

由题意知，函数，满足，

所以函数为奇函数，图象关于原点对称，所以B选项错误；

又因为，所以C选项错误；

又因为，所以D选项错误，

故选：A.

【点睛】

思路点睛：函数图象的辨识可从以下方面入手：

(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．

(2)从函数的单调性，判断图象的变化趋势；

(3)从函数的奇偶性，判断图象的对称性；

(4)从函数的特征点，排除不合要求的图象.

16．（2021·全国高三专题练习）区块链作为一种革新的技术，已经被应用于许多领域.在区块链技术中，若密码的长度设定为256比特，则密码一共有种可能；因此，为了破解密码，最坏情况需要进行次运算.现在有一台机器，每秒能进行次运算，假设机器一直正常运转，那么在最坏情况下这台机器破译密码所需时间大约为（    ）（参考数据：）

A．秒 B．秒 C．秒 D．秒

【答案】B

【分析】

根据题目意思得到，根据对数运算求出 .

【详解】

解：设这台机器破译所需时间大约为秒，

则，两边同时取底数为10的对数

得，

所以，

所以

所以，

所以.

故选：B.

【点睛】

对数运算的一般思路:

（1）拆：首先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后利用对数运算性质化简合并；

（2）合：将对数式化为同底数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算.

二、多选题

17．（2021·全国高一单元测试）若10a＝4，10b＝25，则（    ）

A．a+b＝2 B．b﹣a＝1 C．ab＞8lg22 D．b﹣a＜lg6

【答案】AC

【分析】

由指对互化求出，进而利用对数的运算法则求出a+b和b﹣a的值，可判断ACD，且ab＝2lg2×2lg5＝4lg2•lg5＞4lg2•lg4，可判断C．

【详解】

∵10a＝4，10b＝25，∴a＝lg4，b＝lg25，∴a+b＝lg4+lg25＝lg100＝2，

b﹣a＝lg25﹣lg4＝lg＞lg6，ab＝2lg2×2lg5＝4lg2•lg5＞4lg2•lg4=8lg22．

故选：AC．

18．（2021·全国高三专题练习）已知函数，则下列说法正确的是（    ）

A．函数是偶函数 B．函数是奇函数

C．函数在上为增函数 D．函数的值域为

【答案】AD

【分析】

利用函数单调性的定义及判定方法，可判定A正确，B错误；求得函数的导数，根据导数求得函数的单调性与最值，可判定C不正确，D正确.

【详解】

由题意，函数的定义域为关于原点对称，

又由，

所以函数是偶函数，所以A正确，B错误；

由函数，可得，

当时，，可得，

所以在区间单调递减；

当时，，可得，

所以在区间单调递增，

所以当时，函数取得最小值，最小值为，

所以函数的值域为，所以C不正确，D正确.

故选：AD.

三、填空题

19．（2021·广东深圳市·高三一模）冈珀茨模型是由冈珀茨（Gompertz）提出，可作为动物种群数量变化的模型，并用于描述种群的消亡规律.已知某珍稀物种t年后的种群数量y近似满足冈珀茨模型：（当时，表示2020年初的种群数量），若年后，该物种的种群数量将不足2020年初种群数量的一半，则m的最小值为_________.

【答案】6

【分析】

依题意得通过计算化简得，则问题可解．

【详解】

令由题意知，，

所以 得， 则

所以，解得，所以m的最小值为6

故答案为：6

【点睛】

本题通过实际问题考查指对数不等式，关键要掌握指对数不等式求解法则．

20．（2021·浙江高三专题练习）已知y=f(x)的图象关于坐标原点对称，且对任意的x∈R，f(x+2)=f(-x)恒成立，当时，f(x)=2x，则f(2021)=_____________.

【答案】

【分析】

由已知条件推出函数的周期，利用函数的周期和奇偶性求值即可．

【详解】

y=f(x)的图象关于坐标原点对称，则

又，可得，即的周期为

故答案为：

21．（2021·湖南衡阳市·高三一模）使得“”成立的一个充分条件是___________.

【答案】（答案不唯一，）.

【分析】

由于，故不等式等价于，解得，故只需写出的子集即可.

【详解】

由于，故等价于，解得：，

使得“”成立的一个充分条件只需为集合的子集即可，

故答案可以为：

故答案为：

【点睛】

本题考查充分条件，指数不等式，考查运算求解能力，是中档题.解题的关键在于根据已知解指数不等式，进而需求不等式解集的子集即可.

22．（2021·全国高三专题练习）函数为奇函数，当时，.若，则a的取值范围为______.

【答案】

【分析】

先由函数是奇函数求出，然后讨论的符号求出，再解不等式得出答案.

【详解】

函数为奇函数，则

当时，，则

所以当时，

即，

当时，，则，

由，则，即，解得或

由时，得.

当时，即，则，

由，则，即，解得

由，则此时无解.

当,，即，则，

则不成立.

综上所述：a的取值范围为

故答案为：

【点睛】

关键点睛：本题考查利用奇函数求函数解析式和解不等式，解答本题的关键是先利用奇函数求出，在根据的符号分别求出，在解不等式，属于中档题.