第15讲 概率与统计解答题 2022高考新题好题汇编
展开第15讲 概率与统计解答题
一、解答题
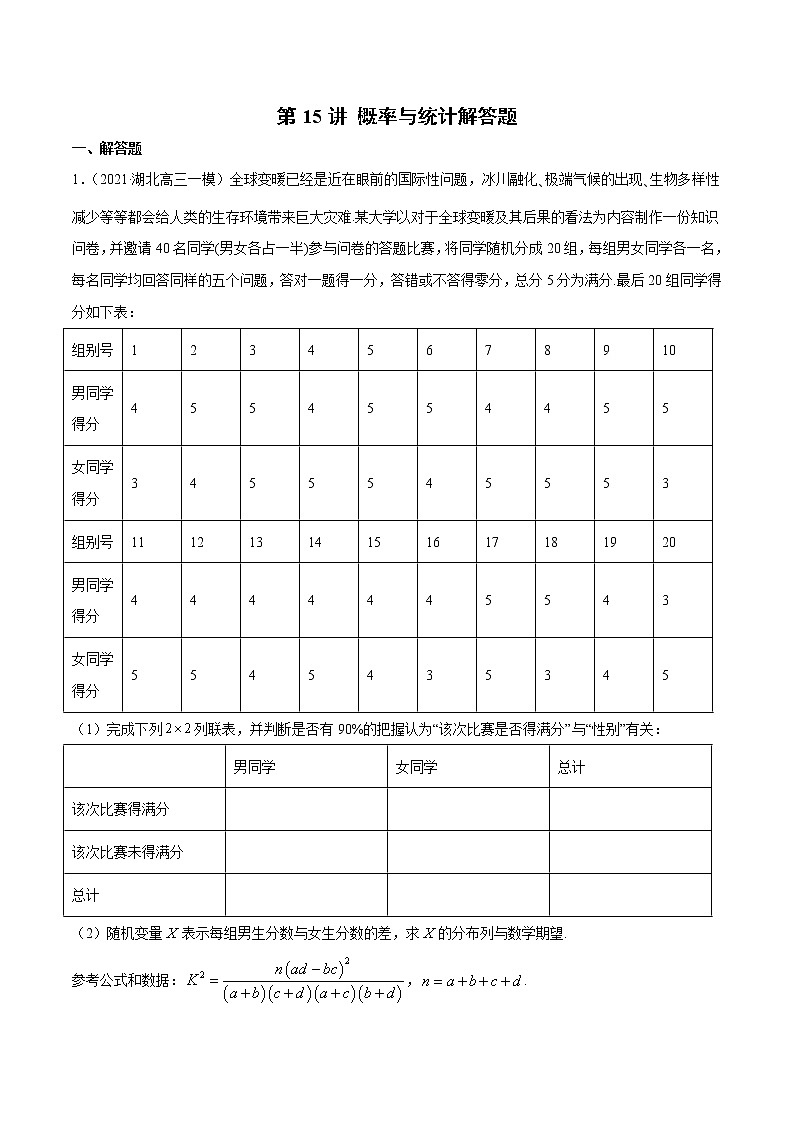
1.(2021·湖北高三一模)全球变暖已经是近在眼前的国际性问题,冰川融化、极端气候的出现、生物多样性减少等等都会给人类的生存环境带来巨大灾难.某大学以对于全球变暖及其后果的看法为内容制作一份知识问卷,并邀请40名同学(男女各占一半)参与问卷的答题比赛,将同学随机分成20组,每组男女同学各一名,每名同学均回答同样的五个问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后20组同学得分如下表:
组别号
1
2
3
4
5
6
7
8
9
10
男同学得分
4
5
5
4
5
5
4
4
5
5
女同学得分
3
4
5
5
5
4
5
5
5
3
组别号
11
12
13
14
15
16
17
18
19
20
男同学得分
4
4
4
4
4
4
5
5
4
3
女同学得分
5
5
4
5
4
3
5
3
4
5
(1)完成下列列联表,并判断是否有90%的把握认为“该次比赛是否得满分”与“性别”有关:
男同学
女同学
总计
该次比赛得满分
该次比赛未得满分
总计
(2)随机变量表示每组男生分数与女生分数的差,求的分布列与数学期望.
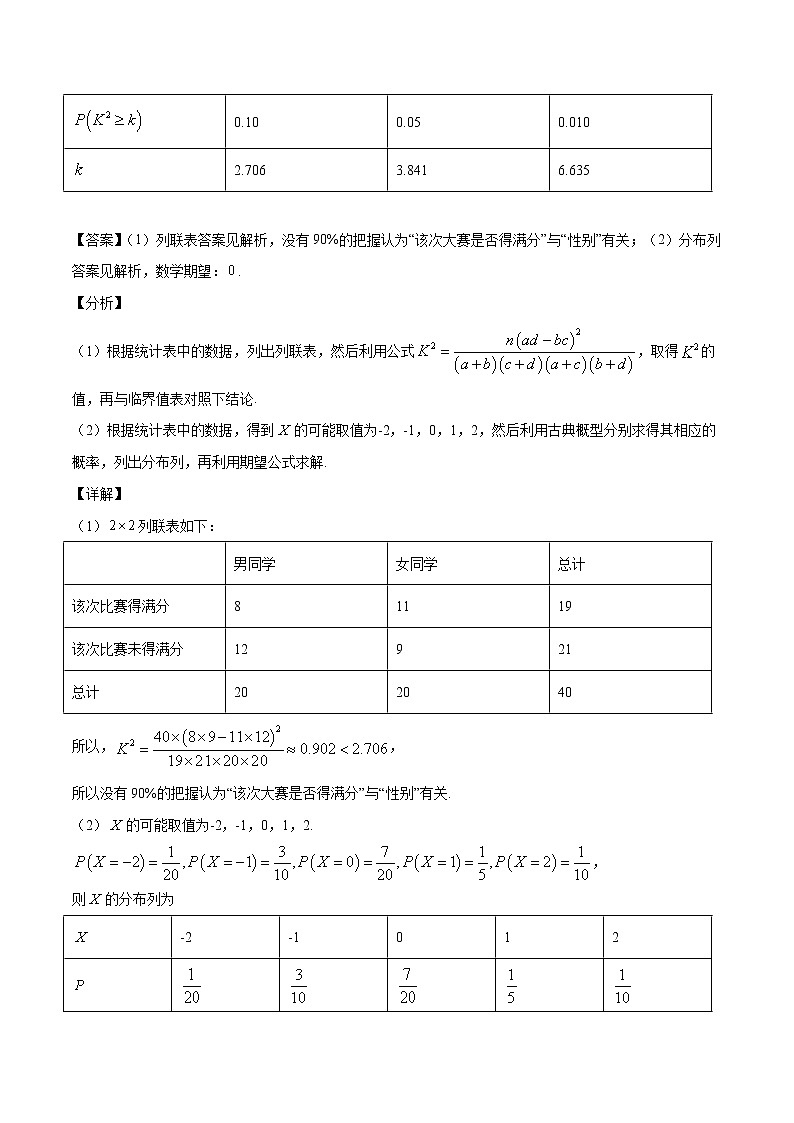
参考公式和数据:,.
0.10
0.05
0.010
2.706
3.841
6.635
【答案】(1)列联表答案见解析,没有90%的把握认为“该次大赛是否得满分”与“性别”有关;(2)分布列答案见解析,数学期望:.
【分析】
(1)根据统计表中的数据,列出列联表,然后利用公式,取得的值,再与临界值表对照下结论.
(2)根据统计表中的数据,得到的可能取值为-2,-1,0,1,2,然后利用古典概型分别求得其相应的概率,列出分布列,再利用期望公式求解.
【详解】
(1)列联表如下:
男同学
女同学
总计
该次比赛得满分
8
11
19
该次比赛未得满分
12
9
21
总计
20
20
40
所以,,
所以没有90%的把握认为“该次大赛是否得满分”与“性别”有关.
(2)的可能取值为-2,-1,0,1,2.
,
则的分布列为
-2
-1
0
1
2
所以.
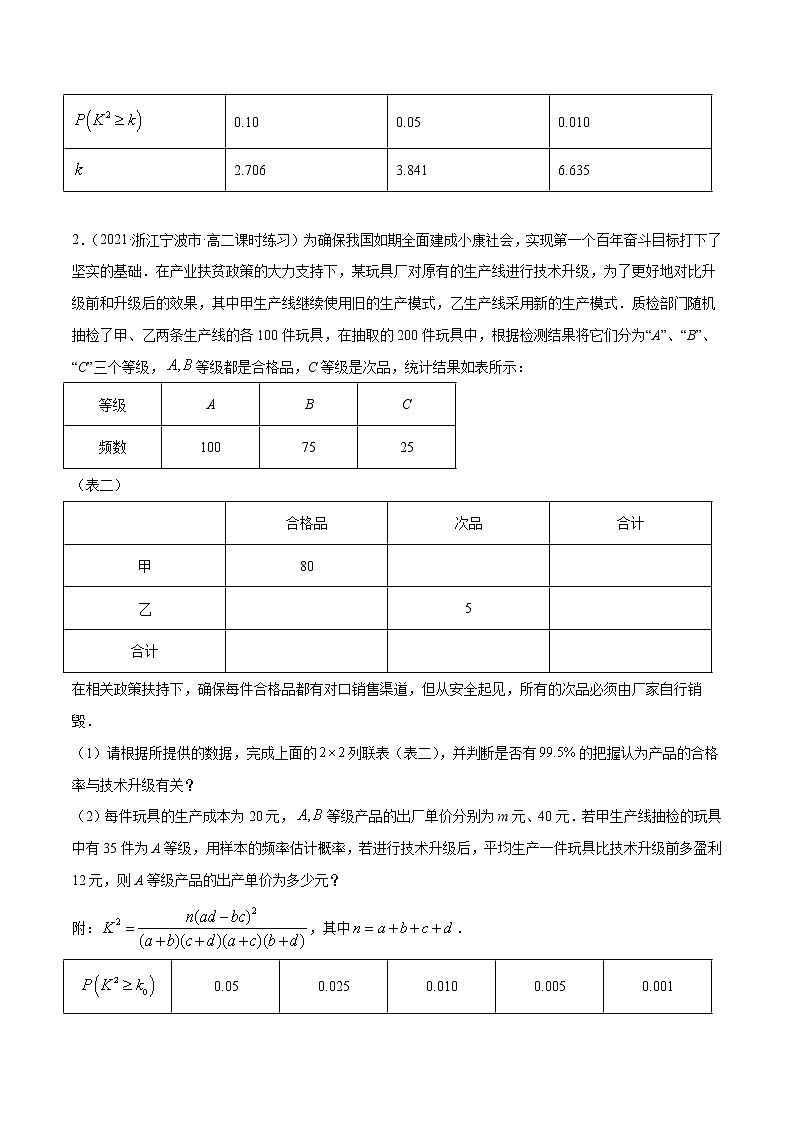
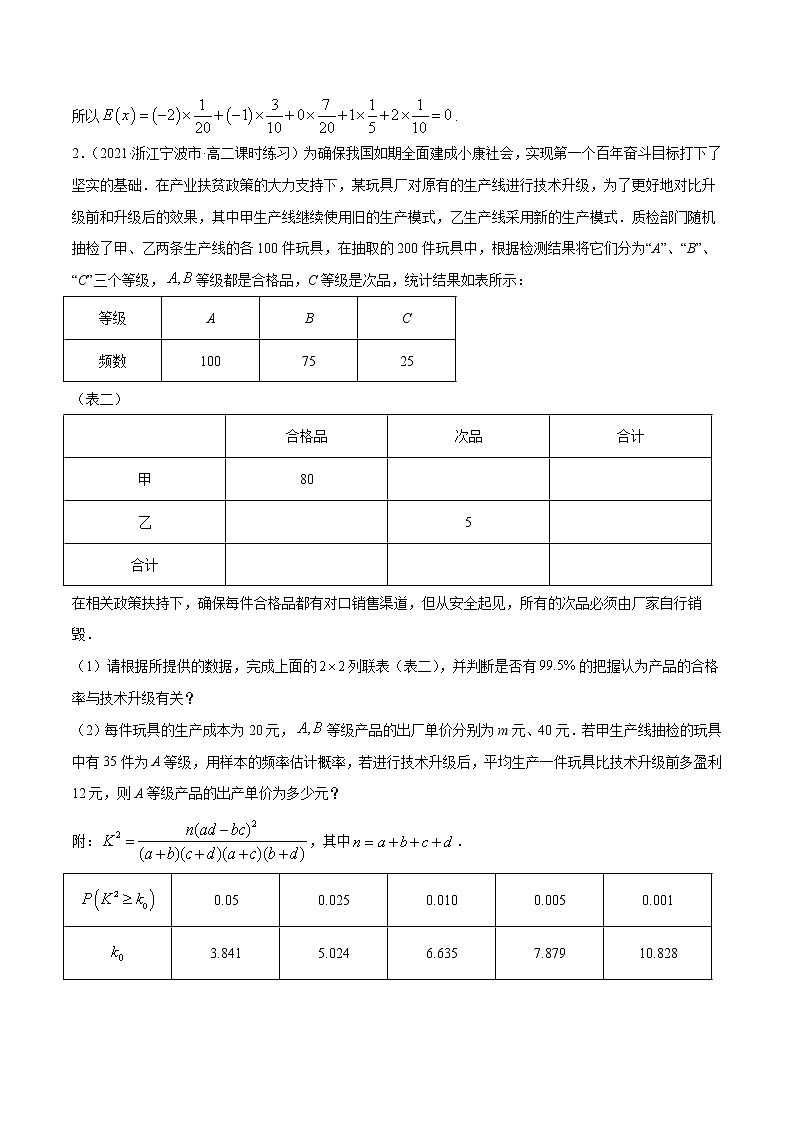
2.(2021·浙江宁波市·高二课时练习)为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础.在产业扶贫政策的大力支持下,某玩具厂对原有的生产线进行技术升级,为了更好地对比升级前和升级后的效果,其中甲生产线继续使用旧的生产模式,乙生产线采用新的生产模式.质检部门随机抽检了甲、乙两条生产线的各100件玩具,在抽取的200件玩具中,根据检测结果将它们分为“A”、“B”、“C”三个等级,等级都是合格品,C等级是次品,统计结果如表所示:
等级
A
B
C
频数
100
75
25
(表二)
合格品
次品
合计
甲
80
乙
5
合计
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由厂家自行销毁.
(1)请根据所提供的数据,完成上面的列联表(表二),并判断是否有的把握认为产品的合格率与技术升级有关?
(2)每件玩具的生产成本为20元,等级产品的出厂单价分别为m元、40元.若甲生产线抽检的玩具中有35件为A等级,用样本的频率估计概率,若进行技术升级后,平均生产一件玩具比技术升级前多盈利12元,则A等级产品的出产单价为多少元?
附:,其中.
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
【答案】(1)列联表见解析;有的把握认为产品的合格率与技术升级有关;(2)60元.
【分析】
(1)由已知数据完成列联表,根据卡方检验公式计算卡方值,结合对照表即可判断产品的合格率与技术升级的相关程度;
(2)法一:由甲乙生产线的数据确定它们取得不同利润的分布列,根据分布列求各自利润的期望值,由求参数m即可;法二:根据甲乙生产线的数据,结合均值的求法求它们的平均值,结合求参数m即可;
【详解】
解:(1)根据所提供的数据,可得列联表:
合格品
次品
合计
甲
80
20
100
乙
95
5
100
合计
175
25
200
设产品的合格率与技术升级无关.
由,
可得.
,故有的把握认为产品的合格率与技术升级有关.
(2)法一:甲生产线抽检的产品中有35件等级,45件等级,20件等级,
对于甲生产线,单件产品利润的取值可能为,
的分布列如下:
20
则,
乙生产线抽检的产品中有65件等级,30件等级,5件等级;
对于乙生产线,单位产品利润的取值可能为,
的分布列如下:
20
则,
依题意.,
,所以,等级产品的出产单价为60元.
法二:甲生产线抽检的产品中有35件等级,45件等级,20件等级,
乙生产线抽检的产品中有65件等级,30件等级,5件等级;
因为用样本的频率估计概率
所以对于甲生产线,单件产品的利润
对于乙生产线,单件产品的利润
依题意.,
,所以,等级产品的出产单价为60元.
【点睛】
关键点点睛:
(1)应用卡方检验公式计算卡方值,比照对照表判断相关性;
(2)应用分布列求期望或直接求数据的平均值,结合已知求参数.
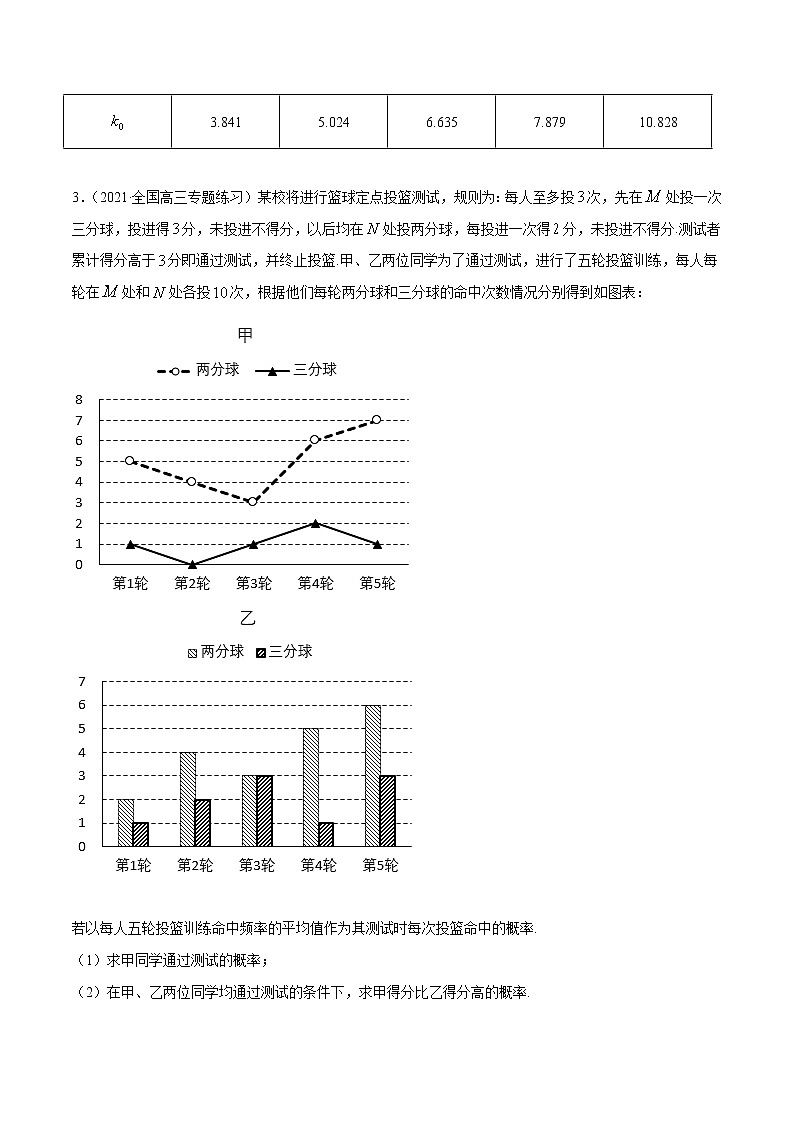
3.(2021·全国高三专题练习)某校将进行篮球定点投篮测试,规则为:每人至多投次,先在处投一次三分球,投进得分,未投进不得分,以后均在处投两分球,每投进一次得分,未投进不得分.测试者累计得分高于分即通过测试,并终止投篮.甲、乙两位同学为了通过测试,进行了五轮投篮训练,每人每轮在处和处各投次,根据他们每轮两分球和三分球的命中次数情况分别得到如图表:
若以每人五轮投篮训练命中频率的平均值作为其测试时每次投篮命中的概率.
(1)求甲同学通过测试的概率;
(2)在甲、乙两位同学均通过测试的条件下,求甲得分比乙得分高的概率.
【答案】(1);(2).
【分析】
(1)记甲同学累计得分为,计算出甲同学两分球和三分球投篮命中的概率,进而可计算得出,即为所求;
(2)设“甲得分比乙得分高”为事件,“甲、乙两位同学均通过了测试”为事件,计算出、,利用条件概率公式可求得,即为所求.
【详解】
(1)甲同学两分球投篮命中的概率为,
甲同学三分球投篮命中的概率为,
设甲同学累计得分为,
则,
所以,甲同学通过测试的概率为;
(2)乙同学两分球投篮命中率为,
乙同学三分球投篮命中率为.
设乙同学累计得分为,则,
,
设“甲得分比乙得分高”为事件,“甲、乙两位同学均通过了测试”为事件,
则,
,
由条件概率公式可得.
【点睛】
思路点睛:用定义法求条件概率的步骤:
(1)分析题意,弄清概率模型;
(2)计算、;
(3)代入公式求.
4.(2021·广东广州市·高三一模)某中学举行篮球趣味投篮比赛,比赛规则如下:每位选手各投5个球,每一个球可以选择在区投篮也可以选择在区投篮,在区每投进一球得2分,投不进球得0分;在区每投进一球得3分,投不进球得0分,得分高的选手胜出.已知参赛选手甲在区和区每次投篮进球的概率分别为和,且各次投篮的结果互不影响.
(1)若甲投篮得分的期望值不低于7分,则甲选择在区投篮的球数最多是多少个?
(2)若甲在区投3个球且在区投2个球,求甲在区投篮得分高于在区投篮得分的概率.
【答案】(1)3;(2)
【分析】
(1)先求出甲在区和在B区投一次得分的期望,设在区投次,计算出总的期望,列出不等式可求;
(2)可得甲在区投篮得分高于在区投篮得分的情况有5种情况,分别求出概率,相加即可得出.
【详解】
(1)甲在区进球的概率为,投进一球得2分,则在区投一次得分的期望为,
同理在B区投一次得分的期望为,
设在区投次,在B区投次,
则总的期望值,解得,
则甲选择在区投篮的球数最多是3个;
(2)由题可得甲在区投3个球,得分可能是0,2,4,6,在区投2个球,得分可能是0,3,6,
则甲在区投篮得分高于在区投篮得分的情况有:
A区2分B区0分,概率为,
A区4分B区0分,概率为,
A区4分B区3分,概率为,
A区6分B区0分,概率为,
A区6分B区3分,概率为,
则甲在区投篮得分高于在区投篮得分的概率为.
【点睛】
关键点睛:本题考查概率的有关计算,解题的关键是正确找出所有的情况,并能争取利用概率公式计算.
5.(2021·全国高三专题练习)某校针对高一学生安排社团活动,周一至周五每天安排一项活动,活动安排表如下:
时间
周一
周二
周三
周四
周五
活动项目
篮球
国画
排球
声乐
书法
要求每位学生选择其中的三项,学生甲决定选择篮球,不选择书法;乙和丙无特殊情况,任选三项.
(1)求甲选排球且乙未选排球的概率;
(2)用X表示甲、乙、丙三人选择排球的人数之和,求X的分布列和数学期望.
【答案】(1);(2)分布列见解析,
【分析】
(1)设事件,分别求出甲、乙同学选排球的概率,由相互独立事件同时发生的概率,即可得出结果.
(2)求出丙同学选排球的概率,X的可能取值为0,1,2,3,分别求出概率,进而可得结果.
【详解】
(1)设A表示事件“甲同学选排球” B表示事件“乙同学选排球”
则
因为事件A,B相互独立,所以甲同学选排球且乙同学未选排球的概率为:
(2)设C表示事件“丙同学选排球”,则
X的可能取值为0,1,2,3则
;
X的分布列为
X
0
1
2
3
P
数学期望为
6.(2021·全国高三专题练习)在一次大范围的随机知识问卷调查中,通过随机抽样,得到参加问卷调查的100人的得分统计结果如下表所示:
得分
频数
2
13
21
25
24
11
4
(1)由频数分布表可以大致认为,此次问卷调查的得分,近似为这100人得分的平均值(同一组中的数据用该组区间的左端点值作代表).
①求的值;
②若,求的值;
(2)在(1)的条件下,为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于的可以获赠2次随机话费,得分低于的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元)
20
50
概率
现有市民甲参加此次问卷调查,记(单位:元)为该市民参加问卷调查获赠的话费,求的分布列与数学期望.
【答案】(1)①;②;(2)分布列答案见解析,数学期望为41.25元.
【分析】
(1)根据题意直接计算平均值即可,再结合正态分布的对称性得到,即得a值;
(2)先根据正态分布知获赠1次和2次随机话费的概率均为,再结合获得随机话费的金额和概率情况写分布列,并计算期望即可.
【详解】
解:(1)①由题意得:,
,
②,
由正态分布曲线的对称性得,,
解得;
(2)由题意得,,即获赠1次和2次随机话费的概率均为,
故获赠话费的的所有可能取值为20,40,50,70,100
,
,
,
,
.
的分布列为:
20
40
50
70
100
元.
所以的数学期望为41.25元.
【点睛】
思路点睛:
求离散型随机变量的分布列及期望的一般步骤:
(1)根据题中条件确定随机变量的可能取值;
(2)求出随机变量所有可能取值对应的概率,即可得出分布列;
(3)根据期望的概念,结合分布列,即可得出期望(在计算时,要注意随机变量是否服从特殊的分布,如超几何分布或二项分布等,可结合其对应的概率计算公式及期望计算公式,简化计算).
7.(2021·全国高三专题练习)太阳能热水器因节能环保而深受广大消费者的青睐,但它也有缺点——持续阴天或雨天便无法正常使用.为了解决这一缺陷,现在的太阳能热水器水箱上都安装了辅助电加热器,如果天气不好或冬季水温无法满足需要时,就可以通过辅助电加热器把水温升高,方便用户使用.某工厂响应“节能减排”的号召,决定把原来给锅炉加热的电热水器更换成电辅式太阳能热水器.电辅式太阳能热水器的耗电情况受当天的日照时长和日均气温影响,假设每天的日照情况和日均气温相互独立,该电辅式太阳能热水器每日耗电情况如下表所示:
日照情况
日均气温不低于15℃
日均气温低于15℃
日照充足
耗电0千瓦时
耗电5千瓦时
日照不足
耗电5千瓦时
耗电10千瓦时
日照严重不足
耗电15千瓦时
耗电20千瓦时
根据调查,当地每天日照充足的概率为,日照不足的概率为,日照严重不足的概率为.2020年这一年的日均气温的频率分布直方图如图所示,区间分组为,,,,,.
(1)求图中的值,并求一年中日均气温不低于15℃的频率;
(2)用频率估计概率,已知该工厂原来的电热水器平均每天耗电20千瓦时,试估计更换电辅式太阳能热水器后这一年能省多少电?(一年以365天计算)
【答案】(1),;(2)千瓦时.
【分析】
(1)根据频率分布直方图中频率和为1求出区间的频率,再除以组距求得的值,再利用长方形面积等于频率,求出不低于15℃的频率;
(2)由(1)知一年中日均气温不低于15℃的概率的估计值为,低于15℃的概率的估计值为,分析题意可知,使用电辅式太阳能热水器日均耗电量的可能取值为0,5,10,15,20,分别算出事件对应的概率,写出分布列,即可得出期望,得到使用电辅式太阳能热水器一天节省的电量,进而得到一年可以节省的电量.
【详解】
(1)依题意得.
一年中日均气温不低于15℃的频率为.
(2)这一年中日均气温不低于15℃的概率的估计值为,一年中日均气温低于15℃的概率的估计值为,
设使用电辅式太阳能热水器日均耗电量为,的所有可能取值为0,5,10,15,20,,,,.
所以的分布列为
0
5
10
15
20
所以的数学期望
所以使用电辅式太阳能热水器一天节省的电量为(千瓦时)
所以使用电辅式太阳能热水器一年节省的电量为(千瓦时)
【点睛】
方法点睛:本题考查离散型随机变量的分布列和数学期望,求离散型随机变量的分布列,首先要根据具体情况确定X的取值情况,然后利用排列,组合,概率知识求出X取各个值时对应的概率,对应服从某种特殊分布的随机变量,其分布列可以直接应用公式给出,考查学生逻辑推理能力与计算能力,属于中档题.
8.(2021·广东梅州市·高三一模)某电子产品加工厂购买配件并进行甲、乙两道工序处理,若这两道工序均处理成功,则该配件加工成型,可以直接进入市场销售;若这两道工序均处理不成功,则该配件报废;若这两道工序只有一道工序处理成功,则该配件需要拿到丙部门检修,若检修合格,则该配件可以进入市场销售,若检修不合格,则该配件报废.根据以往经验,对于任一配件,甲、乙两道工序处理的结果相互独立,且处理成功的概率分别为,,丙部门检修合格的概率为.
(1)求该工厂购买的任一配件可以进入市场销售的概率.
(2)已知配件的购买价格为元/个,甲、乙两道工序的处理成本均为元/个,丙部门的检修成本为元个,若配件加工成型进入市场销售,售价可达元/个;若配件报废,要亏损购买成本以及加工成本.若市场大量需求配件的成型产品,试估计该工厂加工个配件的利润.(利润售价购买价格加工成本)
【答案】(1);(2)万元.
【分析】
(1)根据题意分析出哪种情形下配件可进入市场销售,利用相互独立事件的概率计算公式进行求解即可;
(2)先设工厂加工5000个配件的利润为元,加工一个配件的利润为元,则,再求出的所有可能取值及其对应的概率,进而可得的期望,最后利用数学期望的性质即可得解.
【详解】
(1)记任一配件加工成型可进入市场销售为事件,甲、乙两道工序分别处理成功为事件,,丙部门检修合格为事件.
则.
(2)设该工厂加工个配件的利润为元,加工一个配件的利润为元,则.
由题可知的所有可能取值为,,,,
则,
,
,
.
的分布列为
104
88
∴,
∴.
∴估计该工厂加工个配件的利润为万元.
【点睛】
关键点点睛:求解本题第(2)问的关键是准确求出离散型随机变量的所有取值及其对应的概率,并且在求出分布列后,注意运用分布列的两个性质(①,;②)检验所求的分布列是否正确;(2)在求出后,会利用期望的性质求.
9.(2021·浙江宁波市·高二课时练习)某地发现6名疑似病人中有1人感染病毒,需要通过血清检测确定该感染人员,血清检测结果呈阳性的即为感染人员,呈阴性表示没感染.拟采用两种方案检测:方案甲:将这6名疑似病人血清逐个检测,直到能确定感染人员为止;方案乙:将这6名疑似病人随机分成2组,每组3人.先将其中一组的血清混在一起检测,若结果为阳性,则表示感染人员在该组中,然后再对该组中每份血清逐个检测,直到能确定感染人员为止;若结果为阴性,则对另一组中每份血清逐个检测,直到能确定感染人员为止,
(1)求这两种方案检测次数相同的概率;
(2)如果每次检测的费用相同,请预测哪种方案检测总费用较少?并说明理由.
【答案】(1);(2)乙方案,理由见解析.
【分析】
设甲方案检测的次数,记乙方案检测的次数,
(1)记两种方案检测的次数相同为事件A,根据独立事件的概率的乘法公式,即可求解;
(2)分别求得随机变量和的期望,结合期望的大小,即可求解.
【详解】
由题意可设甲方案检测的次数是X,
则,记乙方案检测的次数是,则,
(1)记两种方案检测的次数相同为事件A,
则,
所以两种方案检测的次数相同的概率为.
(2)由,
所以,
,则,
因为,所以采用乙方案.
【点睛】
求随机变量的期望与方差的方法及步骤:
1、理解随机变量的意义,写出可能的全部值;
2、求取每个值对应的概率,写出随机变量的分布列;
3、由期望和方差的计算公式,求得数学期望;
4、若随机变量的分布列为特殊分布列(如:两点分布、二项分布、超几何分布),可利用特殊分布列的期望和方差的公式求解.
10.(2021·江苏高三专题练习)某市为创建全国文明城市,市文明办举办了一次文明知识网络竞赛,全市市民均有且只有一次参赛机会,满分为100分,得分大于等于80分的为优秀.竞赛结束后,随机抽取了参赛中100人的得分为样本,统计得到样本平均数为71,方差为81.假设该市有10万人参加了该竞赛活动,得分Z服从正态分布.
(1)估计该市这次竞赛活动得分优秀者的人数是多少万人?
(2)该市文明办为调动市民参加竞赛的积极性,制定了如下奖励方案:所有参加竞赛活动者,均可参加“抽奖赢电话费”活动,竞赛得分优秀者可抽奖两次,其余参加者抽奖一次.抽奖者点击抽奖按钮,即随机产生一个两位数(10,11,,99),若产生的两位数的数字相同,则可奖励40元电话费,否则奖励10元电话费.假设参加竞赛活动的所有人均参加了抽奖活动,估计这次活动奖励的电话费总额为多少万元?
参考数据:若,则.
【答案】(1)1.6(万人);(2)150.8万元.
【分析】
(1)由得标准差,所以优秀者得分,由及正态分布的对称性可得答案;
(2)设抽奖一次获得的话费为X元可得X的取值及概率,计算出抽奖一次获得电话费的期望值,再算出抽奖总次数可得答案.
【详解】
(1)因得分,所以标准差,所以优秀者得分,
由得,,
因此,估计这次参加竞赛活动得分优秀者的人数为(万人).
(2)设抽奖一次获得的话费为X元,
则,
所以抽奖一次获得电话费的期望值为,
又由于10万人均参加抽奖,且优秀者参加两次,
所以抽奖总次数为万次,
因此,估计这次活动所需电话费为万元.
【点睛】
本题考查了正态分布的性质及期望,解题的关键点是熟悉正态分布的性质和计算随机变量的取值和概率,考查了的计算能力.
11.(2021·全国高三专题练习(理))某学校共有1000名学生参加知识竞赛,其中男生400人,为了解该校学生在知识竞赛中的情况,采取分层抽样随机抽取了100名学生进行调查,分数分布在分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
将分数不低于750分的学生称为“高分选手”.
(1)求的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从分数落在,内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量,求的分布列及数学期望;
(3)若样本中属于“高分选手”的女生有10人,完成下列列联表,并判断是否有%的把握认为该校学生属于“高分选手”与“性别”有关?
属于“高分选手”
不属于“高分选手”
合计
男生
女生
合计
(参考公式:,期中)
【答案】(1),中位数650,众数600;(2)分布列见解析;期望为;(3)填表见解析;有.
【分析】
(1)由频率分布直方图中频率和为1可求得,每组数据用该组区间的中点值乘以频率相加得均值;
(2)由频率分布直方图知从,中抽取7人,从,中抽取3人,随机变量的所有可能取值有0,1,2,3,求出各概率得分布列,然后由期望公式得期望;
(3)样本中男生40人,女生60人属于“高消费群”的25人,其中女生10人,由频率分布直方图求出高消费群人数,可得高消费群中男生人数,从而可填写列联表,并计算出后可得结论.
【详解】
(1)由题意知,
解得,
样本平均数为,
中位数650,众数600.
(2)由题意,从中抽取7人,从中抽取3人,
随机变量的所有可能取值有0,1,2,3.
,
所以随机变量的分布列为:
0
1
2
3
随机变量的数学期望.
(3)由题可知,样本中男生40人,女姓60人,属于“高分选手”的25人,其中女姓10人;得出以下列联表;
属于“高分选手”
不属于“高分选手”
合计
男生
15
25
40
女生
10
50
60
合计
25
75
100
,
所以有%的把握认为该校学生属于“高分选手”与性别有关.
【点睛】
超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.超几何分布的特征是:①考查对象分两类;②已知各类对象的个数;③从中抽取若干个个体,考查某类个体个数X的概率分布,超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.
12.(2021·辽宁沈阳市·高三一模)习近平总书记曾提出,“没有全民健康,就没有全面小康”.为响应总书记的号召,某社区开展了“健康身体,从我做起”社区健身活动.运动分为徒手运动和器械运动两大类.该社区对参与活动的人进行了调查,其中男性人,女性人,所得统计数据如下表所示:(单位:人)
性别
器械类
徒手类
合计
男性
女性
合计
(1)请将题中表格补充完整,并判断能否有99%把握认为“是否选择器械类与性别有关”?
(2)为了检验活动效果,该社区组织了一次竞赛活动.竞赛包括三个项目,一个是器械类,两个是徒手类,规定参与者必需三个项日都参加.据以往经验,参赛者通过器械类竞赛的概率是,通过徒手类竞赛的概率都是,且各项目是否通过相互独立.用表示某居民在这次竞赛中通过的项目个数,求随机变量的分布列和数学期望.
(参考数据:)
附:
【答案】(1)表格见解析,有;(2)答案见解析,.
【分析】
(1)根据男性人,女性人和表中已有的数据完成表格即可;利用 求得的值,再与临界值标对照下结论.
(2)易知随机变量的所有可能取值有,再分别求得相应的概率,列出分布列,根据分布列再去期望.
【详解】
(1)根据器械类总人数人,其中男性人,可得女性为人,
根据总人数人,得到徒手类总人数人,其中女性人,可得男性人.
完成表格如下:
性别
器械类
徒手类
合计
男性
女性
合计
所以,
所以,有把握认为“是否选择物理类与性别有关”.
(2)随机变量的所有可能取值有.
因为
所以的分布列为
所以数学期望.
【点睛】
方法点睛:求解离散型随机变量X的分布列的步骤:①理解X的意义,写出X可能取的全部值;②求X取每个值的概率;③写出X的分布列.求离散型随机变量的分布列的关键是求随机变量所取值对应的概率.
13.(2021·全国高三专题练习)据调查,目前对于已经近视的小学生,有两种配戴眼镜的选择,一种是佩戴传统的框架眼镜;另一种是佩戴角膜塑形镜,这种眼镜是晚上睡觉时佩戴的一种特殊的隐形眼镜(因其在一定程度上可以减缓近视的发展速度越来越多的小学生家长选择角膜塑形镜控制孩子的近视发展),市从该地区小学生中随机抽取容量为的样本,其中因近视佩戴眼镜的有人(其中佩戴角膜塑形镜的有人,其中名是男生,名是女生).
(1)若从样本中选一位学生,已知这位小学生戴眼镜,那么,他戴的是角膜塑形镜的概率是多大?
(2)从这名戴角膜塑形镜的学生中,选出个人,求其中男生人数的分布列;
(3)若将样本的频率当做估计总体的概率,请问,从市的小学生中,随机选出位小学生,求佩戴角膜塑形镜的人数的期望和方差.
【答案】(1);(2)分布列答案见解析;(3)期望是,方差是.
【分析】
(1)先根据该市的样本求得这位学生佩戴眼镜的概率和佩戴眼镜是角塑性眼镜的概率,再利用条件概率的计算公式计算即得结果;
(2)从8名学生选3个,男生人数X服从超几何分布,按照,k=0,1,2,写出分布列即可;
(3)依题意随机变量服从二项分布,利用公式计算期望和方差即可.
【详解】
解:(1)根据题中样本数据,设“这位小学生佩戴眼镜”为事件A,则,
“这位小学生佩戴的眼镜是角膜塑形镜”为事件,则“这位小学生佩戴眼镜,且眼镜是角膜塑形镜”为事件,则,
故所求的概率为: ,
所以从样本中选一位学生,已知这位小学生戴眼镜,则他戴的是角膜塑形镜的概率是;
(2)依题意,佩戴角膜塑形镜的有人,其中名是男生,名是女生,故从中抽3人,男生人数X的所有可能取值分别为0,1,2,
其中:;
;
.
所以男生人数的分布列为:
(3)由已知可得:
则:,
所以佩戴角膜塑形镜的人数的期望是,方差是.
【点睛】
思路点睛:
求离散型随机变量的分布列及期望的一般步骤:
(1)根据题中条件确定随机变量的可能取值;
(2)求出随机变量所有可能取值对应的概率,即可得出分布列;
(3)根据期望的概念,结合分布列,即可得出期望(在计算时,要注意随机变量是否服从特殊的分布,如超几何分布或二项分布等,可结合其对应的概率计算公式及期望计算公式,简化计算).
14.(2021·河南高三月考(理))为了树立和践行绿水青山就是金山银山的理念,加强环境的治理和生态的修复,某市在其辖区内某一个县的27个行政村中各随机选择农田土壤样本一份,对样本中的铅、锦、铭等重金属的含量进行了检测,并按照国家土壤重金属污染评价级标准(清洁、尚清洁、轻度污染、中度污染、重度污染)进行分级,绘制了如图所示的条形图
(1)从轻度污染以上(包括轻度污染)的行政村中按分层抽样的方法抽取6个,求在轻度、中度、重度污染的行政村中分别抽取的个数;
(2)规定:轻度污染记污染度为1,中度污染记污染度为2,重度污染记污染度为3.从(1)中抽取的6个行政村中任选3个,污染度的得分之和记为X,求X的数学期望.
【答案】(1)从轻度污染的行政村中抽取个,从中度污染的行政村中抽取个,从重度污染的行政村中抽取个;(2)5.
【分析】
(1)根据题意,轻度污染以上(包括轻度污染)的行政村共个,再根据分层抽样分别算出所抽取的轻度污染、中度污染、重度污染行政村的个数即可;
(2)X的所有可能取值为3,4,5,6,7,写出每算出一个数据的概率,得出分布列,再根据期望公式即可得解.
【详解】
(1)轻度污染以上(包括轻度污染)的行政村共个,
所以从轻度污染的行政村中抽取个,从中度污染的行政村中抽取个,从重度污染的行政村中抽取个.
(2)X的所有可能取值为3,4,5,6,7.
,
,
,
,
.
所以X的分布列为
X
3
4
5
6
7
P
所以.
15.(2021·浙江宁波市·高二课时练习)某电器企业统计了近年的年利润额(千万元)与投入的年广告费用(十万元)的相关数据,散点图如图,对数据作出如下处理:令,,得到相关数据如表所示:
(1)从①;②;③三个函数中选择一个作为年广告费用和年利润额的回归类型,判断哪个类型符合,不必说明理由;
(2)根据(1)中选择的回归类型,求出与的回归方程;
(3)预计要使年利润额突破亿,下一年应至少投入多少广告费用?(结果保留到万元)
参考数据:,.
参考公式:回归方程中斜率和截距的最小二乘估计公式分别为,.
【答案】(1)选择回归类型更好;(2);(3)下一年应至少投入万元广告费用.
【分析】
(1)根据散点图的形状可选择合适的函数模型;
(2)作变换,,将表格中数据代入最小二乘法公式,求出、的值,进而可得出关于的回归方程;
(3)令,结合参考数据解出的范围,由此可得出结论.
【详解】
解:(1)由散点图知,年广告费用和年利润额的回归类型并不是直线型的,而是曲线型的,且与呈正相关.
所以选择回归类型更好;
(2)对两边取自然对数,得,
,,则,
由表中数据得,,
所以,所以,
所以年广告费用和年利润额的回归方程为;
(3)由(2),知,令,得,得,
所以, 所以(十万元).
故下一年应至少投入万元广告费用.
【点睛】
关键点点睛:本题考查非线性回归模型的应用,解决本题的关键就是对非线性回归函数模型作变换,将其转化为线性回归函数模型,结合最小二乘法求解.
16.(2021·全国高三专题练习)槟榔芋又名香芋,衡阳市境内主要产于祁东县.槟榔芋富含淀粉、蛋白质、脂肪和多种维生素,可加工成芋兰片,芋丝等副食品,深受广大消费者喜爱.衡阳市某超市购进一批祁东槟榔芋,并随机抽取了50个统计其质量,得到的结果如下表所示:
质量/克
数量/个
2
5
12
22
6
3
(1)若购进这批槟榔芋100千克,同一组数据用该区间中点值作代表,试估计这批槟榔芋的数量(所得结果四舍五入保留整数);
(2)以频率估计概率,若在购进的这批槟榔芋中,随机挑选3个,记3个槟榔芋中质量在间的槟榔芋数量为随机变量,求的分布列和数学期望.
【答案】(1)517;(2)分布列见解析,0.3.
【分析】
(1)由统计表计算出平均质量,然后可得个数.
(2)所有可能取值为0,1,2,3,而一个槟榔芋质量在间概率由表格可得,然后计算出各概率可得概率分布列,再由期望公式计算期望.
【详解】
(1)设50个槟榔芋中,每个槟榔芋的平均质量为,则
(克)
所以这批槟榔芋的数量约为(个)
(2)所有可能取值为0,1,2,3.
由表中数据可知,任意挑选一个槟榔芋,质量在的概率为
所以,,
,,
故的分布列为:
0
1
2
3
0.729
0.243
0.027
0.001
.
17.(2021·全国高三专题练习)某商城玩具柜台元旦期间促销,购买甲、乙系列的盲盒,并且集齐所有的产品就可以赠送元旦礼品.而每个甲系列盲盒可以开出玩偶,,中的一个,每个乙系列盲盒可以开出玩偶,中的一个.
(1)记事件:一次性购买个甲系列盲盒后集齐,,玩偶;事件:一次性购买个乙系列盲盒后集齐,玩偶;求概率及;
(2)礼品店限量出售甲、乙两个系列的盲盒,每个消费者每天只有一次购买机会,且购买时,只能选择其中一个系列的一个盲盒.通过统计发现:第一次购买盲盒的消费者购买甲系列的概率为,购买乙系列的概率为;而前一次购买甲系列的消费者下一次购买甲系列的概率为,购买乙系列的概率为;前一次购买乙系列的消费者下一次购买甲系列的概率为,购买乙系列的概率为;如此往复,记某人第次购买甲系列的概率为.
①;
②若每天购买盲盒的人数约为100,且这100人都已购买过很多次这两个系列的盲盒,试估计该礼品店每天应准备甲、乙两个系列的盲盒各多少个.
【答案】(1),;(2)①;②应准备甲系列盲盒40个,乙系列盲盒60个.
【分析】
(1)根据题意,集齐,,玩偶的个数可以分三类情况:,, 玩偶中,每个均有出现两次、,, 玩偶中,一个出现一次,一个出现两次,一个出现三次、,, 玩偶中,两个出现一次,另一个出现四次讨论计算,并根据古典概率计算即可;对于,先考虑一次性购买个乙系列盲盒没有集齐,玩偶的概率再求解.
(2)①根据题意,,当时,,再根据数列知识计算即可;
②由①得购买甲系列的概率近似于,故用表示一天中购买甲系列盲盒的人数,则,再根据二项分布的期望计算即可.
【详解】
解:(1)由题意基本事件共有:种情况,
其中集齐,,玩偶的个数可以分三类情况,
,, 玩偶中,每个均有出现两次,共种;
,, 玩偶中,一个出现一次,一个出现两次,一个出现三次,共种;
,, 玩偶中,两个出现一次,另一个出现四次,共种;
故.
根据题意,先考虑一次性购买个乙系列盲盒没有集齐,玩偶的概率,即,
所以.
(2)①由题意可知:,当时,,
∴,
所以是以为首项,为公比的等比数列,
∴,
②因为每天购买盲盒的100人都已购买过很多次,
所以,对于每一个人来说,某天来购买盲盒时,可以看作n趋向无穷大,
所以购买甲系列的概率近似于,假设用表示一天中购买甲系列盲盒的人数,则,
所以,即购买甲系列的人数的期望为40,
所以礼品店应准备甲系列盲盒40个,乙系列盲盒60个.
【点睛】
本题考查排列组合,数列递推关系,二项分布的数学期望等,考查运算求解能力,是中档题.本题第一问解题的关键在于根据题意,分类计数,注意考虑全面,避免重漏,第二问解题的关键在于根据题意得关于的递推关系,进而利用数列知识求解.
18.(2021·全国高三专题练习)2020年国庆节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握国庆节期间车辆出行的高峰情况,在某高速公路收费站点记录了3日上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费站点,它们通过该收费站点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作、9:40~10:00记作,10:00~10:20记作,10:20~10:40记作,例如:10点04分,记作时刻64.
(Ⅰ)估计这600辆车在9:20~10:40时间内通过该收费站点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(Ⅱ)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列;
(Ⅲ)根据大数据分析,车辆在每天通过该收费站点的时刻T服从正态分布,其中可用3日数据中的600辆车在9:20~10:40之间通过该收费站点的时刻的平均值近似代替,用样本的方差近似代替(同一组中的数据用该组区间的中点值代表).假如4日全天共有1000辆车通过该收费站点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
附:若随机变量T服从正态分布,则,,.
【答案】(Ⅰ)10:04;(Ⅱ)答案见解析;(Ⅲ)819.
【分析】
(Ⅰ)结合频率分布直方图,利用平均数公式求解.
(Ⅱ)结合频率分布直方图,利用分层抽样的方法可知,抽取的10辆车中,在这一区间内的车辆数为,则 X的可能的取值为0,1,2,3,4,再分别求得相应的概率,列出分布列.
(Ⅲ)由(1)得,再利用频率分布直方图求得,然后利用原则求解.
【详解】
(Ⅰ)这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为:
,即10∶04
(Ⅱ)由频率分布直方图和分层抽样的方法可知,抽取的10辆车中,在10:00前通过的车辆数就是位于时间分组中在[20,60)这一区间内的车辆数,
即,
所以X的可能的取值为0,1,2,3,4.
所以, ,,
, .
所以X的分布列为:
X
0
1
2
3
4
P
(Ⅲ)由(1)得,
所以,
估计在9:46~10:40之间通过的车辆数也就是在46,100通过的车辆数,
由,得
,
所以估计在在9:46~10:40之间通过的车辆数为.
【点睛】
方法点睛:(1)求解离散型随机变量X的分布列的步骤:①理解X的意义,写出X可能取的全部值;②求X取每个值的概率;③写出X的分布列.(2)求离散型随机变量的分布列的关键是求随机变量所取值对应的概率,在求解时,要注意应用计数原理、古典概型等知识.
第13讲 数列解答题 2022高考新题好题汇编: 这是一份第13讲 数列解答题 2022高考新题好题汇编,文件包含第13讲数列解答题解析版docx、第13讲数列解答题原卷版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
第12讲 解三角形解答题 2022高考新题好题汇编: 这是一份第12讲 解三角形解答题 2022高考新题好题汇编,文件包含第12讲解三角形解答题解析版pdf、第12讲解三角形解答题原卷版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
第11讲 复数小题 2022高考新题好题汇编: 这是一份第11讲 复数小题 2022高考新题好题汇编,文件包含第11讲复数小题解析版docx、第11讲复数小题原卷版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。












