
初中数学人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线导学案
展开专题四 平行线几何模型-平行线+角平分线(巩固篇)
(专项练习)
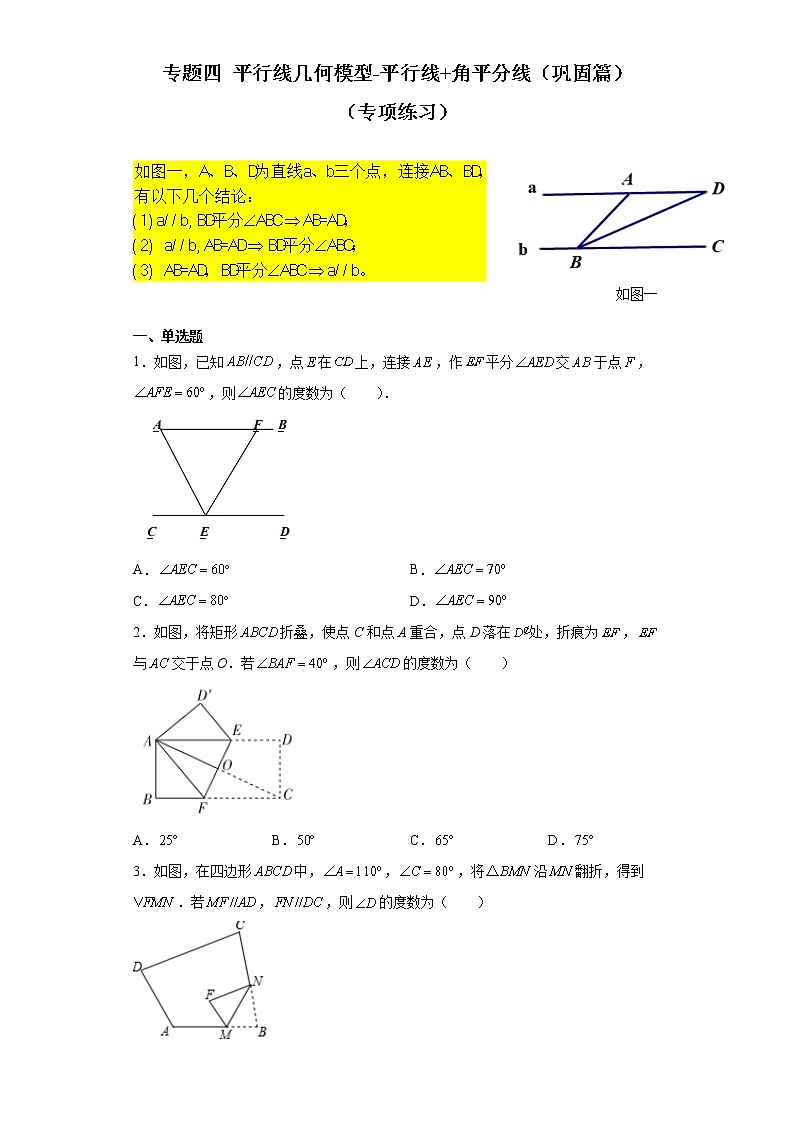
如图一
一、单选题
1.如图,已知,点在上,连接,作平分交于点,,则的度数为( ).
A. B.
C. D.
2.如图,将矩形折叠,使点C和点A重合,点D落在处,折痕为,与交于点O.若,则的度数为( )
A. B. C. D.
3.如图,在四边形中,,,将沿翻折,得到.若,,则的度数为( )
A. B. C. D.
4.如图,直线,点是上一点,的角平分线交于点,若,,则的大小为( )
A.136° B.138° C.140° D.148°
5.如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6.如图,将长方形纸片ABCD,沿折痕MN折叠,B分别落在A1,B1的位置,A1B1交AD于点E,若∠BNM=65°,以下结论:①∠B1NC=50°;②∠A1ME=50°;③A1M∥B1N;④∠DEB1=40°.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
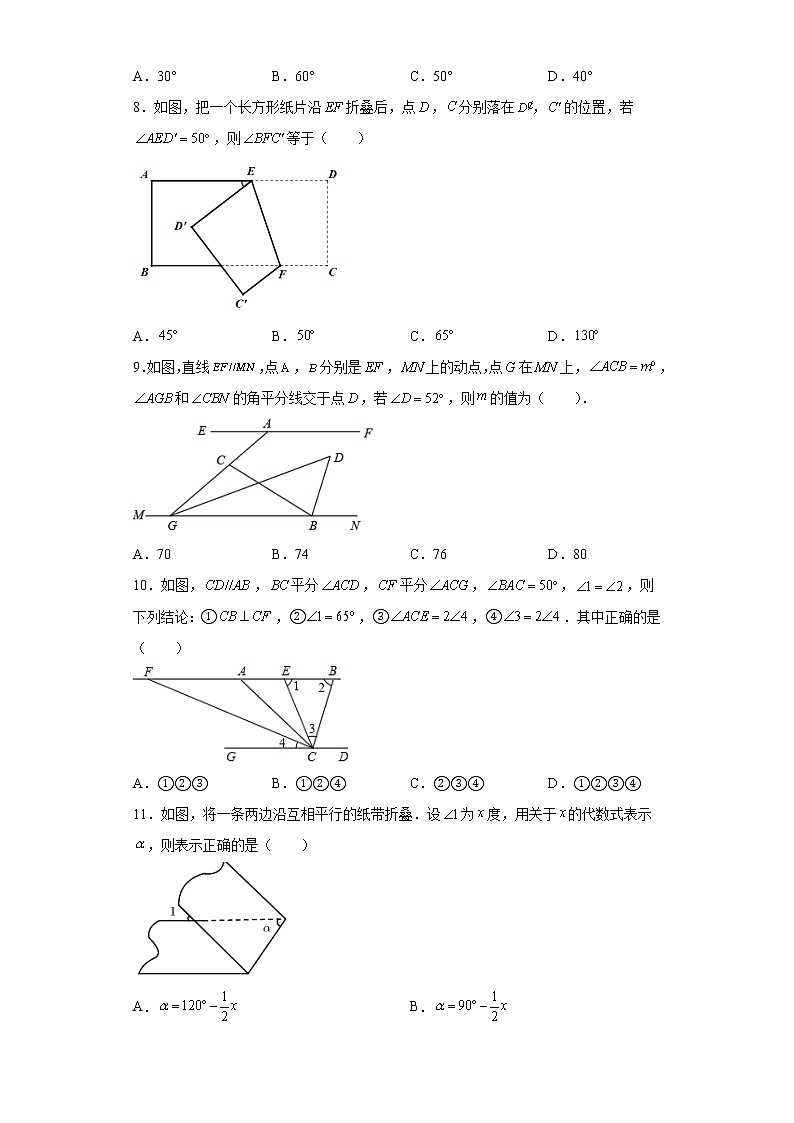
7.如图,ABCD,E为CD上的一点,射线EF经过点A,EC=EA,若∠ACE=30°,则∠BAF=( )
A.30° B.60° C.50° D.40°
8.如图,把一个长方形纸片沿折叠后,点,分别落在,的位置,若,则等于( )
A. B. C. D.
9.如图,直线,点,分别是,上的动点,点在上,,和的角平分线交于点,若,则的值为( ).
A.70 B.74 C.76 D.80
10.如图,,平分,平分,,,则下列结论:①,②,③,④.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
11.如图,将一条两边沿互相平行的纸带折叠.设为度,用关于的代数式表示,则表示正确的是( )
A. B.
C. D.
12.如图,平分平分,则下列结论:①;②;③;④其中正确结论有( )个.
A. B. C. D.4
13.如图,若平分平分,则的度数( )
A. B. C. D.
14.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
15.如图,已知长方形纸片ABCD, 点E、F在BC边上,点G、H在AD边上,分别沿EG、FH折叠,使点B和点C都落在点M处,若a +β=224°,则∠EMF的度数为( )
A.90° B.91° C.92° D.94°
16.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
17.如图,已知,平分,平分,则下列判断:①;②平分;③;④中,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
18.如图将一条两边互相平行的纸带按如图折叠,若∠EFG+∠EGD=150°,则∠EGD=_____
19.如图,四边形中,,连接,平分,E是直线上一点,,,则的长为________.
20.如图,正方形ABCD中,BD为对角线,且BE为∠ABD的角平分线,并交CD延长线于点E,则∠E=______°.
21.如图ABDE,BF平分∠ABC,反向延长射线BF,与∠EDC的平分线DG相交于点P,若∠BPD=44°,则∠C=___.
22.如图,已知ACBD,BC平分∠ABD,CE平分∠DCM,且BC⊥CE.则下列结论:①CB平分∠ACD,②ABCD,③∠A=∠BDC,④点P是线段BE上任意一点,则∠APM=∠BAP+∠PCD.正确的是______.
23.如图,,的平分线交于点,是上的一点,的平分线交于点,且,下列结论:①平分;②;③与互余的角有2个;④若,则.其中正确的是______(请把正确结论的序号都填上)
24.如图,已知AB∥EF,点O在两平行线之间,点C在直线AB上,连接OC,OE,恰好CO平分∠ACD,OG在∠COE的内部,OI、OH分别平分∠COG、∠EOG.若∠BCD=50°,∠E=75°,则∠IOH的度数是___.
25.如图,∠MAN=52°,过射线AM上一点C作CP∥AN,依次作出∠BCP的角平分线CB,CB2,∠Bn﹣1CP的角平分线CB,其中点B、B1、B2、....Bn﹣1、Bn,都在射线AN上,若∠PCBn=1°时,则n=___.
26.如图,己知,点在上,点为平面内一点,,过点作平分平分,若,则__________.
27.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为__度.
28.如图,已知直线,直线分别是截线,,分别平分.则_______.
29.如图,于C,E是上一点,,平分平分,则:与之间的数最关系为______.
30.如图,,平分,平分,若设,则______度(用x,y的代数式表示),若平分,平分,可得,平分,平分,可得…,依次平分下去,则_____度.
31.已知,,将一副三角板按照如图方式摆放在平行线之间,且线段BC落在直线MN上,线段DE落在直线PQ上,其中,,CO平分,EO平分,两条角平分线相交与点O,则________.
32.如图,已知,,平分,则________.
33.如图,点P、Q分别在一组平行直线、上,在两直线间取一点E使得,点F、G分别在、的角平分线上,且点F、G均在平行直线、之间,则__________.
参考答案
1.A
【分析】
由平行线的性质可得,再由角平分线性质可得,利用邻补角可求的度数.
【详解】
解:,,
,
平分交于点,
,
.
故选:A.
【点拨】本题主要考查平行线的性质及角平分线的定义,解答的关键是熟记并灵活运用平行线的性质.
2.C
【分析】
根据折叠的性质可得:,由等边对等角得出,再依据三角形内角和得出,根据三角形外角和定理可得,最后依据矩形及平行线的性质即可得出答案.
【详解】
解:∵将矩形ABCD沿着EF折叠,
∴,
∴,
∵,
∴,
∴,
∴,
∵四边形ABCD为矩形,
∴ADBC,
∴,
故选:C.
【点拨】题目主要考查折叠的性质、三角形外角和定理及平行线的性质等知识点,熟练掌握各知识点并融会贯通是解题关键.
3.B
【分析】
首先利用平行线的性质得出∠BMF=110°,∠FNB=80°,再利用翻折变换的性质得出∠FMN=∠BMN=55°,∠FNM=∠MNB=40°,进而求出∠B的度数,进而即可求解.
【详解】
解:∵MF∥AD,FN∥DC,∠A=110°,∠C=80°,
∴∠BMF=110°,∠FNB=80°,
∵将△BMN沿MN翻折得△FMN,
∴∠FMN=∠BMN=55°,∠FNM=∠MNB=40°,
∴∠D=∠B=180°−55°−40°=85°,
故选:B.
【点拨】此题主要考查了平行线的性质,折叠的性质以及多边形内角和定理以及翻折变换的性质,得出∠FMN=∠BMN,∠FNM=∠MNB是解题关键.
4.D
【分析】
作辅助线,构建三角形,根据平行线的性质可得∠MAB=∠BAC=64°,根据三角形外角的性质可得结论.
【详解】
解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°-116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2-∠1=116°-20°=96°,
∴∠ADC=180°-96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
【点拨】本题主要考查了平行线的性质,三角形外角性质的综合应用,解题时注意:两直线平行,同旁内角互补.
5.A
【分析】
根据AB∥CD可得∠BOD=∠ABO=40°,利用平角得到∠COB=140°,再根据角平分线的定义得到∠BOE=70°,则③正确;利用OP⊥CD,AB∥CD,∠ABO=40°,可得∠POB=50°,∠BOF=20°,∠FOD=20°,进而可得OF平分∠BOD,则①正确;由∠EOB=70°,∠POB=50°,∠POE=20°,由∠BOF=∠POF-∠POB=20°,进而可得∠POE=∠BOF,则②正确;由②可知∠POB=50°,∠FOD=20°,则④不正确.
【详解】
③∵AB∥CD,
∴∠BOD=∠ABO=40°,
∴∠COB=180°-40°=140°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=×140°=70°,
故③正确;
①∵OP⊥CD,
∴∠POD=90°,
又∵AB∥CD,
∴∠BPO=90°,
又∵∠ABO=40°,
∴∠POB=90°-40°=50°,
∴∠BOF=∠POF-∠POB=70°-50°=20°,
∠FOD=40°-20°=20°,
∴OF平分∠BOD,
故①正确;
②∵∠EOB=70°,∠POB=90°-40°=50°,
∴∠POE=70°-50°=20°,
又∵∠BOF=∠POF-∠POB=70°-50°=20°,
∴∠POE=∠BOF,
故②正确;
④由①可知∠POB=90°-40°=50°,
∠FOD=40°-20°=20°,
故∠POB≠2∠DOF,
故④不正确.
故结论正确的是①②③,
故选A.
【点拨】本题考查了平行线的性质,解题的关键是要注意将垂直、平行、角平分线的定义结合应用,弄清图中线段和角的关系,再进行解答.
6.D
【分析】
由折叠的性质可得∠B1NM=∠BNM=65°,再根据平角的定义可得∠B1NC,故可判断①;根据平行线的性质可得∠AMN=115°,由折叠得∠A1MN=115°,依据∠AMN+∠A1MN-180°=50°可判断②;由∠B1NM+∠A1MN=180°可判断③;根据直角三角形的两个锐角互余可得④.
【详解】
解:在长方形纸片ABCD中,∠A=90°,AD∥BC,
∴∠BNM+∠AMN=180°,
∵∠BNM=65°,
∴∠AMN=115°,
由折叠的性质可得:∠B1NM=∠BNM=65°,∠AMN=∠A1MN=115°,
∵∠BNM+∠B1NM+∠B1NC=180°,
∴∠B1NC=50°;故①正确;
∵∠AMN=∠A1MN=115°,
∴∠A1ME=∠AMN+∠A1MN-180°=50°,故②正确;
∵∠A1MN=115°,∠B1NM=65°,
∴∠B1NM+∠A1MN=180°,
∴A1M∥B1N,故③正确;
∵∠A1=∠A=90°,
∴∠A1ME+∠A1EM=90°,
∵∠A1ME=50°,
∴∠DEB1=∠A1EM=40°,故④正确;
故选D.
【点拨】本题主要考查折叠的性质、平行线的性质与判定及直角三角形的两个锐角互余,熟练掌握折叠的性质、平行线的性质与判定及直角三角形的两个锐角互余是解题的关键.
7.B
【分析】
先根据EC=EA,∠ACE=30°得出∠CAE=30°,再由三角形外角的性质得出∠AED的度数,最后利用平行线的性质即可得出结论.
【详解】
解:∵EC=EA.∠ACE=30°,
∴∠CAE=∠ACE=30°,
∴∠AED=∠CAE+∠ACE=30°+30°=60°.
∵ABCD,
∴∠BAF=∠AED=60°.
故选:B.
【点拨】本题考查的是等腰三角形的性质,三角形的外角性质及平行线的性质,熟练掌握相关图形的性质是解决本题的关键.
8.B
【分析】
由折叠的性质可得∠DEF=∠D′EF,因为∠AED′=50°,结合平角可求得∠DEF=∠D′EF=65°,再结合平行可求得和的度数,则即可求得答案.
【详解】
解:,
,
长方形纸片沿EF折叠后,点D、C分别落在、的位置,
,
∵AD∥BC,∥,
∴,
∴,
故选:B.
【点拨】本题主要考查平行线的性质及折叠的性质,掌握两直线平行内错角相等,同旁内角互补是解题的关键.
9.C
【分析】
先由平行线的性质得到∠ACB=∠5+∠1+∠2,再由三角形内角和定理和角平分线的定义求出m即可.
【详解】
解:过C作CH∥MN,
∴∠6=∠5,∠7=∠1+∠2,
∵∠ACB=∠6+∠7,
∴∠ACB=∠5+∠1+∠2,
∵∠D=52°,
∴∠1+∠5+∠3=180°−52°=128°,
由题意可得GD为∠AGB的角平分线,BD为∠CBN的角平分线,
∴∠1=∠2,∠3=∠4,
∴m°=∠1+∠2+∠5=2∠1+∠5,∠4=∠1+∠D=∠1+52°,
∴∠3=∠4=∠1+52°,
∴∠1+∠5+∠3=∠1+∠5+∠1+52°=2∠1+∠5+52°=m°+52°,
∴m°+52°=128°,
∴m°=76°.
故选:C.
【点拨】本题主要考查平行线的性质和角平分线的定义,关键是对知识的掌握和灵活运用.
10.B
【分析】
根据角平分线的性质可得,,,再利用平角定义可得∠BCF=90°,进而可得①正确;首先计算出∠ACB的度数,再利用平行线的性质可得∠2的度数,从而可得∠1的度数;利用三角形内角和计算出∠3的度数,然后计算出∠ACE的度数,可分析出③错误;根据∠3和∠4的度数可得④正确.
【详解】
解:如图,
∵BC平分∠ACD,CF平分∠ACG,
∴
∵∠ACG+∠ACD=180°,
∴∠ACF+∠ACB=90°,
∴CB⊥CF,故①正确,
∵CD∥AB,∠BAC=50°,
∴∠ACG=50°,
∴∠ACF=∠4=25°,
∴∠ACB=90°-25°=65°,
∴∠BCD=65°,
∵CD∥AB,
∴∠2=∠BCD=65°,
∵∠1=∠2,
∴∠1=65°,故②正确;
∵∠BCD=65°,
∴∠ACB=65°,
∵∠1=∠2=65°,
∴∠3=50°,
∴∠ACE=15°,
∴③∠ACE=2∠4错误;
∵∠4=25°,∠3=50°,
∴∠3=2∠4,故④正确,
故选:B.
【点拨】此题主要考查了平行线的性质,以及角平分线的性质,关键是理清图中角之间的和差关系.
11.B
【分析】
利用平行线的性质以及翻折不变性解决问题即可.
【详解】
解:如图,//,
,
将一条上下两边互相平行的纸带折叠
,
,
故选:B.
【点拨】本题考查了平行线的性质、翻折变换等知识,解题关键是熟练掌握基本知识.
12.B
【分析】
根据平行线的性质、角平分线的定义和垂直定义进行求解判断即可.
【详解】
解:∵AB∥CD,∠ABO=50°,
∴∠ABO+∠BOC=180°,∠ABO=∠BOD=50°,
∴∠BOC=180°﹣∠ABO=130°,
∵OE平分∠BOC,OF平分∠BOD,
∴∠BOE=∠COE=∠BOC=65°,故①错误;
∠BOF=∠DOF=∠BOD=25°,
∴∠EOF=∠BOE+∠BOF=65°+25°=90°,
∴OF⊥OE,故②正确;
∵OP⊥CD,
∴∠POC=∠POD=90°,
∴∠POE=90°﹣∠COE=90°﹣65°=25°,
∠POB=90°﹣∠BOD=90°﹣50°=40°,
∴∠POE=∠BOF,故③正确;
∠POB≠2∠DOF,故④错误,
综上,正确结论有②③共2个,
故选:B.
【点拨】本题考查平行线的性质、角平分线的定义和垂直定义,熟练掌握这些知识的联系和运用是解答的关键.
13.C
【分析】
根据平行线的性质得到∠AEF+∠EFC=180°,∠BEF+∠EFD=180°,∠AEN=∠ENF,根据角平分线的定义得到∠BEM=∠FEM,∠EFM=∠DFM,求得∠FEM+∠EFM=90°,根据垂直的定义得到EM⊥FM,根据平行线的性质得到∠ENF=∠MFD,等量代换得到∠MFD=40°.
【详解】
解:∵AB//CD,
∴∠BEF+∠EFD=180°,∠AEN=∠ENF,
∵EM平分∠BEF,FM平分∠EFD,
∴∠BEM=∠FEM,∠EFM=∠DFM,
∴∠FEM+∠EFM=90°,
∴∠M=90°,
∴EM⊥FM,
∵NE⊥EM,
∴EN//MF,
∴∠ENF=∠MFD,
∵∠AEN=40°,
∴∠ENF=∠AEN=40°,
∴∠MFD=40°,
故选:C.
【点拨】此题考查了平行线的判定和性质,根据平行线的判定定理证得EN∥MF是解本题的关键.
14.C
【分析】
根据平行线的性质、角平分线的性质和三角形内角和定理计算即可;
【详解】
∵CE⊥直线c于点E,∠1=24°,
∴,
∵a∥b,
∴,
又∵BC平分∠ABD,
∴,
∴;
故答案选C.
【点拨】本题主要考查了平行线的性质、角平分线的性质和三角形内角和定理,准确计算是解题的关键.
15.C
【分析】
根据四边形ABCD是长方形,可得AD∥BC,得到∠BEG+α=180°,∠CFH+β=180°,进而得到∠BEG+∠CFH=360°-(α+β)=136°,由折叠性质可知,∠BEG=∠GEM,∠CFH=∠HFM,进而得到∠BEM+∠CFM=272°,根据平角的定义列式得到∠MEF+∠MFE=88°,再根据三角形的内角和即可得解.
【详解】
解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠BEG+α=180°,∠CFH+β=180°,
∴∠BEG=180°-α,∠CFH=180°-β,
∵α+β=224°,
∴∠BEG+∠CFH=360°-(α+β)=136°,
由折叠可知:
∠BEG=∠GEM,∠CFH=∠HFM,
∴∠BEM+∠CFM=2(∠BEG+∠CFH)=272°,
∴∠MEF+∠MFE=360°-(∠BEM+∠CFM)=360°-272°=88°,
∴∠EMF=180°-(∠MEF+∠MFE)=92°,
故选:C.
【点拨】本题考查了平行线的性质,解决本题的关键是熟练掌握平行线的性质及三角形的内角和.
16.A
【分析】
①证明AB∥CD,可做判断;
②根据平行线的判定和性质可做判断;
③根据AF∥ED得内错角相等和同位角相等,再由角平分线的定义得∠ADE=∠CDE,从而可做判断.
【详解】
解:①∵AB⊥BC,DC⊥BC,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
故①正确;
②∵AB∥CD,
∴∠AFD+∠BAF=180°,
∵∠BAF=∠EDF,
∴∠AFD+∠EDF=180°,
∴AF∥DE,
故②正确;
③∵AF∥ED,
∴∠DAF=∠ADE,∠F=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F,
故③正确;
故选:A.
【点拨】本题考查了平行线的判定与性质,角平分线的定义,熟知平行线的判定定理与性质是解题的关键.
17.B
【分析】
根据平行线的性质求出,根据角平分线定义和平行线的性质求出,推出,再根据平行线的性质判断即可.
【详解】
∵,
∴,∴正确;
∵,
∴,
∵平分,平分,
∴,,
∴,
∴,
∴,
∴根据已知不能推出,∴错误;错误;
∵,,
∴,
∵,
∴,
∴,∴正确;
即正确的有个,
故选:.
【点拨】本题考查了平行线的性质和判定,角平分线定义的应用,能灵活运用平行线的性质和判定进行推理是解此题的关键.
18.
【分析】
先根据平行线的性质得到,结合已知∠EFG+∠EGD=150°,解得∠EGD=,再根据折叠的性质解得,结合两直线平行,同旁内角互补得到,据此整理得,进而解题.
【详解】
解:
∠EFG+∠EGD=150°,
∠EGD=
折叠
故答案为:.
【点拨】本题考查折叠的性质、平行线的性质等知识,两直线平行,同旁内角互补,掌握相关知识是解题关键.
19.6或10
【分析】
先利用平行线的性质和等角对等边的性质得到AB=AD,再根据点E在D的左边和右边分别求解即可;
【详解】
∵平分,
∴,
∵,
∴,
∴,
∴是等腰三角形,
∴,
当点E在线段AD上时,
∵,,
∴,
当点E在线段AD延长线上时,
∵,,
∴;
故答案是:6或10.
【点拨】本题主要考查了平行线的性质,角平分线的定义,等角对等边,先证出AB=AD是解题的关键.
20.22.5
【分析】
由平行线的性质可知,由角平分线的定义得,进而可求∠E的度数.
【详解】
解:为正方形,
,,
,
平分,
,
又,
,
故答案为:22.5.
【点拨】本题考查了正方形的性质,平行线的性质,角平分线的定义,熟练掌握正方形的性质是解答本题的关键.
21.92°
【分析】
延长AB交PD与点M,过点C作CNAB,根据角平分线可设∠ABF=∠FBC=x,∠CDP=∠EDP=y,根据平行线的性质可得∠AMD=∠EDP=y,再根据三角形的外角性质可得y-x=44°,根据平行线的性质可得∠NCD=180°-2y,∠NCB=2x,最后根据∠BCD=∠NCD+∠NCB即可求得答案.
【详解】
解:如图,延长AB交PD与点M,过点C作CNAB,
∵BF平分∠ABC,DG平分∠EDC,
∴设∠ABF=∠FBC=x,∠CDP=∠EDP=y,
∴∠MBP=∠ABF=x,
∵ABDE,
∴∠AMD=∠EDP=y,
∵∠AMD=∠BPD+∠MBP,∠BPD=44°,
∴y=44°+x,
∴y-x=44°,
∵ABDE,CNAB,
∴CNDE,
∴∠CDE+∠NCD=180°,
∴∠NCD=180°-∠CDE=180°-2y,
∵CNAB,
∴∠NCB=∠ABC=2x,
∴∠BCD=∠NCD+∠NCB
=180°-2y+2x
=180°-2(y-x)
=180°-2×44°
=92°,
故答案为:92°.
【点拨】本题考查了平行线的性质及平行公理的推理,三角形的外角性质,角平分线的定义,正确作出辅助线并熟练掌握平行线的性质是解决本题的关键.
22.①②③
【分析】
根据平行线的判定与性质和角平分线的定义逐一进行判断即可.
【详解】
解:如图,
∵ACBD,
∵∠2=∠3
∵BC平分∠ABD,
∴∠1=∠2,
∴∠1=∠3,
∵CE平分∠DCM,
∴∠4=∠5,
∵BC⊥CE.
∴∠4+∠6=90°,
∴∠5+∠6=90°,
∵∠3+∠5=90°,
∴∠3=∠6,
∴CB平分∠ACD,故①正确;
∴∠1=∠6,
ABCD,故②正确;
∴四边形ABCD是平行四边形,
∴∠A=∠BDC,故③正确;
如图,点P是线段BE上任意一点,
∵AB与PC不平行,CD与PM不平行,
∴∠BAP≠∠APC,∠PCD≠∠CPM,
∴∠APM≠∠BAP+∠PCD.故④不正确.
所以正确的是①②③.
故答案为:①②③.
【点拨】本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
23.①②
【分析】
求出∠EBD+∠ABC=90°,∠DBG+∠CBG=90°,求出∠ABC=∠GBC,根据角平分线的定义即可判断①;根据平行线的性质得出∠ABC=∠BCG,求出∠ACB=∠GBC,根据平行线的判定即可判断②;根据余角的定义即可判断③;根据平行线的性质得出∠EBG=∠A=α,求出∠EBD=∠EBG=α,根据平行线的性质得出∠EBD+∠BDF=180°,即可判断④.
【详解】
∵BD⊥BC,
∴∠DBC=90°,
∴∠EBD+∠ABC=180°﹣90°=90°,∠DBG+∠CBG=90°,
∵BD平分∠EBG,
∴∠EBD=∠DBG,
∴∠ABC=∠GBC,
即BC平分∠ABG,故①正确;
∵AE∥CF,
∴∠ABC=∠BCG,
∵CB平分∠ACF,
∴∠ACB=∠BCG,
∵∠ABC=∠GBC,
∴∠ACB=∠GBC,
∴AC∥BG,故②正确;
与∠DBE互余的角有∠ABC,∠CBG,∠ACB,∠BCG,共4个,故③错误;
∵AC∥BG,∠A=α,
∴∠EBG=∠A=α,
∵∠EBD=∠DBG,
∴∠EBD=∠EBG=α,
∵AB∥CF,
∴∠EBD+∠BDF=180°,
∴∠BDF=180°﹣∠EBD=180°﹣α,
若,
则,
解得
则
,矛盾,
故④错误;
故答案为:①②.
【点拨】本题考查了平行线的性质和判定,角平分线的定义等知识点,能灵活运用定理进行推理是解此题的关键.
24.85°
【分析】
延长CO,交FE的延长线与点M,容易求出∠CMF=65°,根据三角形的外角求出∠MOE=10°,再根据邻补角及角平分线的定义求解即可.
【详解】
解:延长CO,交FE的延长线与点M,
∵∠BCD=50°,
∴∠ACD=180°-∠BCD=130°,
∵CO平分∠ACD,
∴∠ACM=∠ACD=65°,
∵AB∥EF,
∴∠CMF=∠ACM=65°,
∵∠QEF=∠CMF+∠MOE,∠QEF=75°,
∴∠MOE=75°-65°=10°,
∴∠COE=180°-∠MOE=170°,
∵OI、OH分别平分∠COG、∠EOG,
∴∠IOH=∠IOG+∠GOH=∠COE=85°,
故答案为:85°.
【点拨】本题考查了平行线的性质,角平分线的定义,熟练掌握性质定理及作出正确的辅助线是解题的关键.
25.6
【分析】
根据角平分线的定义和平行线的性质求得的度数规律,然后代入求解.
【详解】
解:,
,
平分,
,
又平分,
,
.
,
,,
,
解得:,
故答案为:6.
【点拨】本题考查角平分线的定义,平行线的性质,掌握两直线平行,同位角相等,理解角平分线的概念,并通过探索发现题目数量间蕴含的规律是解题关键.
26.
【分析】
设,则,通过角的关系转化,可得,三角形内角和定理可得,求得目标角,再根据已知条件,求得即可求得.
【详解】
设
平分
,
平分
在中
,
即
解得
故答案为:
【点拨】本题考查了角平分线的定义,垂直的定义,三角形内角和定理,平行线的性质,找到是解题的关键.
27.59或121
【分析】
分两种情况:①当射线GP⊥EG于点G时,∠PGE=90°,②当射线GP′⊥EG于点G时,∠P′GE=90°,根据平行线的判定与性质和角平分线定义即可求出∠PGF的度数.
【详解】
解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF==31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
【点拨】本题主要考查了平行线的性质和角平分线的定义,准确计算是解题的关键.
28.165°
【分析】
过点E作,结合可得,根据角平分线的定义可得,,再根据平行线的性质可得,,由此即可求得答案.
【详解】
解:如图,过点E作,
又∵,
∴,
∵分别平分,,
∴,,
∵,
∴,
∵,
∴,
∴,
故答案为:165°.
【点拨】本题考查了平行线的判定与性质,角平分线的定义,熟练掌握平行线的判定与性质是解决本题的关键.
29.2∠H+∠ACF=180°
【分析】
延长EC,交DH于K,根据三角形外角的性质,平行线的性质即可得到90°+∠ACE=45°+∠ACE+∠H,从而求得∠ACE,进而即可求得∠H与∠ACF之间的数量关系.
【详解】
解:延长EC,交DH于K,
∵∠EKD=∠HEC+∠H,∠ECD=∠EKD+∠HDC,
∴∠ECD=∠HEC+∠HDC+∠H,
∵DF∥AB,
∴∠B=∠BDG,
∵EH平分∠BEC,DH平分∠BDG,
∴∠HEC=∠BEC,∠HDC=∠B,
∵∠BEC=∠A+∠ACE,
∴∠HEC=∠A+∠ACE,
∴∠ECD=∠A+∠ACE+∠B+∠H,
∵AC⊥BD,
∴∠A+∠B=90°,
∴∠ECD=45°+∠ACE+∠H,
∵AC⊥BD,
∴∠ECD=90°+∠ACE,
∴90°+∠ACE=45°+∠ACE+∠H,
∴90°+∠ACE=2∠H,
∴90°+(90°-∠ACF)=2∠H,即2∠H+∠ACF=180°,
故答案为:2∠H+∠ACF=180°.
【点拨】本题考查了平行线的性质,角平分线的定义以及三角形外角的性质,是基础题.
30.
【分析】
过点P1作PG∥AB∥CD,根据平行线的性质:两直线平行,内错角相等即可证得,再根据角平分线的定义总结规律可得.
【详解】
解:过点作∥AB,可得∥CD,
设,,
∴,,
∴;
同理可得:,,...,
∵平分,平分,
∴,
,
...,
∴,
故答案为:,.
【点拨】本题考查了平行线性质的应用和角平分线的定义,解题的关键是学会添加常用辅助线,构造平行线解决问题,学会探究规律,利用规律解决问题,属于中考常考题型.
31.52.5
【分析】
延长CO交PQ于点F,根据∠COE=∠CFE+∠OEF,结合平行线的性质,角的平分线的定义计算;
【详解】
延长CO交PQ于点F,则∠COE=∠CFE+∠OEF,
∵,,CO平分,EO平分,
∴∠BCF=30°,∠OEF=22.5°,
∵,
∴∠BCF=∠CFE,
∴∠COE=30°+22.5°=52.5°,
故答案为:52.5°.
【点拨】本题考查了平行线的性质,角的平分线的定义,三角形外角定理,延长构造三角形外角,活用平行线的性质是解题的关键.
32.64°.
【分析】
由角平分线的性质和平行线的性质,即可求出答案.
【详解】
解:∵AD∥BC,∠B=32°,
∴∠ADB=∠B=32°.
∵DB平分∠ADE,
∴∠ADE=2∠ADB=64°,
∵AD∥BC,
∴∠DEC=∠ADE=64°.
故答案为:64°.
【点拨】本题考查了平行线的性质和角平分线的性质,解题的关键是熟练掌握所学的知识进行解题.
33.35°
【分析】
过点F作,过点G作,利用平行线的性质和角平分线的定义即可求解.
【详解】
过点F作,过点G作,
∵平分,平分,
设,,
∵
∴,
∴,
∵,
∴,
∴,,,
∴
故.
【点拨】本题考查平行线的性质,根据题意作出平行线是解题的关键.
数学人教版第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线导学案及答案: 这是一份数学人教版第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线导学案及答案,共35页。学案主要包含了单选题,填空题等内容,欢迎下载使用。
初中人教版5.2.1 平行线导学案: 这是一份初中人教版5.2.1 平行线导学案,共38页。学案主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线学案: 这是一份人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线学案,共59页。学案主要包含了单选题,解答题等内容,欢迎下载使用。













