数学人教版第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线导学案及答案

这是一份数学人教版第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线导学案及答案，共35页。学案主要包含了单选题，填空题等内容，欢迎下载使用。
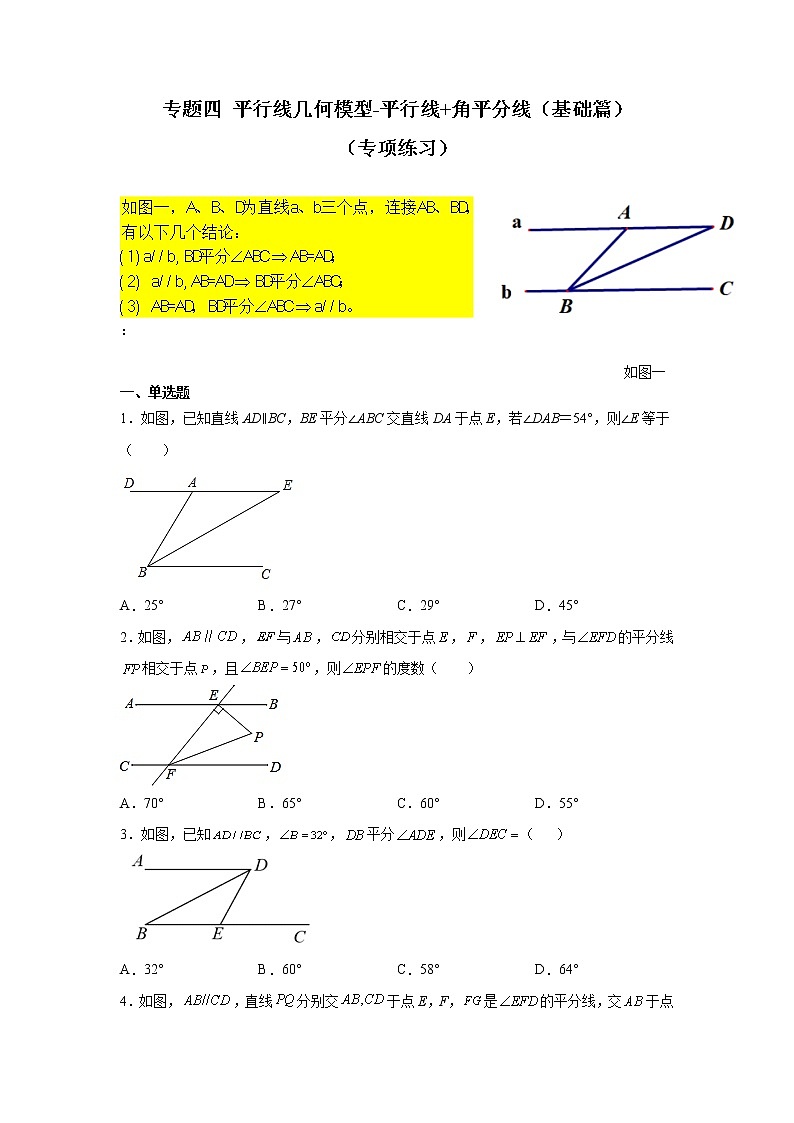
专题四 平行线几何模型-平行线+角平分线（基础篇）
（专项练习）

：

如图一
一、单选题
1．如图，已知直线AD∥BC，BE平分∠ABC交直线DA于点E，若∠DAB＝54°，则∠E等于（ ）

A．25° B．27° C．29° D．45°
2．如图，，与，分别相交于点，，，与的平分线相交于点，且，则的度数（ ）

A．70° B．65° C．60° D．55°
3．如图，已知，，平分，则（ ）

A．32° B．60° C．58° D．64°
4．如图，，直线分别交于点E，F，是的平分线，交于点G，若，那么等于（ ）

A． B． C． D．
5．如图，，平分交于点，，，，分别是，延长线上的点，和的平分线交于点．下列结论：
①； ②；
③平分； ④．
其中正确的有（ ）

A．个 B．个 C．个 D．个
6．如图，，平分，，则的度数为（ ）

A． B． C． D．
7．如图，已知，平分，，则的度数是（ ）

A． B． C． D．
8．如图，直线AB∥CD，EF分别交AB、CD于E、F两点，作∠BEF、∠DFE的平分线相交于点K；作∠BEK、∠DFK的平分线相交于点K1；依此类推，作∠BEK1、∠DFK2的平分线相交于点K2，…，作∠BEKn﹣1、∠DFKn﹣1的平分线相交于点Kn，则∠Kn的与∠K的关系为（　　）

A． ∠Kn＝∠K B．∠Kn＝∠K
B． C．∠Kn＝∠K D．∠Kn＝∠K
9．如图，直线AB∥CD，BE平分∠ABD，若∠DBE＝20°，∠DEB＝80°，求∠CDE的度数是（　　）

A．50° B．60° C．70° D．80°
10．如图，AB∥CD，∠FGB＝146°，FG平分∠EFD，则∠AEF的度数等（　　）

A．34° B．68° C．46° D．92°
11．如图，AB∥CD，直线EF分别交AB、CD于点E、F，FH平分∠EFD，若∠1＝110°，则∠2的度数为（　　）

A．45° B．40° C．55° D．35°
12．如图，，直线分别交直线，于点，，平分，若，则的度数为（ ）

A． B． C． D．
13．如图，，平分，，则的度数是（ ）

A． B． C． D．
14．如图，直线AB∥CD，点P在直线AB、CD之间，点E、Q分别在AB、CD上．连接PE、PQ，∠AEP＜90°，EF平分∠PEB交CD于点F，PQ∥EF．∠EPQ＝100°，则∠CQP的度数是（ ）

A．80° B．70° C．60° D．50°
15．如图，已知，的两个顶点分别在直线，上，，交于点，若平分，．则的度数为（ ）

A． B． C． D．
16．如图，ABCD，∠FEB=70°，∠EFD的角平分线FG交AB于点G，则∠GFD的度数为（ ）

A．63° B．53° C．65° D．55°


二、填空题
17．如图，AC平分∠DAB，∠1＝∠2，试说明．

证明：∵AC平分∠DAB（_______），
∴∠1＝∠______（________），
又∵∠1＝∠2（________），
∴∠2＝∠______（________），
∴AB______（________）．
18．如图，将一副三角板按如图所示放置，，，，且，则下列结论中：①；②若平分，则有；③将三角形绕点旋转，使得点落在线段上，则此时；④若，则．其中结论正确的选项有______．（写出所有正确结论的序号）

19．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=40°，则∠AEC=_____度．

20．如图，，，BE平分交AD于点E，连接CE，AF交CD的延长线于点F，，若，，则的度数为______．

21．如图，已知ABCD，BE平分∠ABC，DE平分∠ADC，若∠ABC =m°，∠ADC =n°，则∠E=_________°．

22．如图，BD平分，，，要使，则______°．

23．如图，正方形ABCD中，BD为对角线，且BE为∠ABD的角平分线，并交CD延长线于点E，则∠E＝______°．

24．如图，AD是∠EAC的平分线，AD∥BC，∠B＝40°，则∠DAC的度数为____．

25．如图，OP平分∠AOB，∠AOP=15°，PC∥OA，PD⊥OA于点D，PC=6，则PD=___________．

26．如图①，已知，，的交点为，现作如下操作：第一次操作，分别作和的平分线，交点为；第二次操作，分别作和的平分线，交点为；第三次操作，分别作和的平分线，交点为……第次操作，分别作和的平分线，交点为．如图②，若，则的度数是__________．

27．如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝40°，则下列结论：①∠BOE＝70°；②OF平分∠BOD；③∠1＝∠2；④∠POB＝2∠3．其中正确的结论有______．（填序号）

28．已知：AB∥CD，点C在点D的右侧，BE平分∠ABC，DE平分∠ADC，BE，DE所在直线交于点E，∠ADC＝70°．

（1）∠CDE＝________度 ；
（2）若∠ABC＝n°，则∠BED的度数是________（用含n的式子表示）
29．如图，，，为射线上一点，平分，、交于点，点在线段延长线上时，连接，若，，则的度数为__________．

30．如图，已知∠A＝（60﹣x）°，∠ADC＝（120+x）°，∠CDB＝∠CBD，BE平分∠CBF，若∠DBE＝59°，则∠DFB＝___．

31．如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②∠BFD＝45°；③∠ADC＝∠GCD；④CA平分∠BCG．其中正确的结论是______（填序号）．

32．如图，已知AB∥CE，∠B＝50°，CE平分∠ACD，则∠ACD＝__°

33．已知，，，点，在上，平分，且，下列结论正确得是：__________．

①； ②；
③； ④若，则.
34．已知：如图，平分，，，，则___．









参考答案
1．B
【分析】
根据两直线平行，内错角相等可求∠ABC=54°，再根据角平分线的性质可求∠EBC=27°，再根据两直线平行，内错角相等可求∠E．
【详解】
解：∵AD∥BC，
∴∠ABC=∠DAB=54°，∠EBC=∠E，
∵BE平分∠ABC，
∴∠EBC=∠ABC=27°，
∴∠E=27°．
故选：B．
【点拨】本题考查了平行线的性质，角平分线，关键是求出∠EBC=27°．
2．A
【分析】
利用平行线的性质与垂直的性质求解 再利用角平分线的含义求解 再利用三角形的内角和定理可得答案.
【详解】
解： ，


平分，


故选A
【点拨】本题考查的是垂直的定义，平行线的性质，角平分线的定义，三角形的内角和定理，熟悉以上知识，掌握基本的逻辑推理是解题的关键.
3．D
【分析】
先根据平行线的性质（两直线平行，内错角相等），可得∠ADB=∠B，再利用角平分线的性质可得：∠ADE=2∠ADB=64°，最后再利用平行线的性质（两直线平行，内错角相等）即可求出答案．
【详解】
解：∵AD∥BC，∠B=32°，
∴∠ADB=∠B=32° ．
∵DB平分∠ADE，
∴∠ADE=2∠ADB=64°，
∵AD∥BC，
∴∠DEC=∠ADE=64°．
故选：D．
【点拨】题目主要考查了平行线的性质和角平分线的性质，解题的关键是熟练掌握平行线的性质，找出题中所需的角与已知角之间的关系．
4．C
【分析】
由，，即可求得的度数，又由是的平分线，即可求得的度数，然后由，根据两直线平行，同旁内角互补，即可求得的度数．
【详解】
解：∵
∴
∵，
∴，
是的平分线，
，
∵，
∴
．
故选：C．
【点拨】本题考查了平行线的性质与邻补角的定义，角平分线的定义，掌握两直线平行，同旁内角互补定理的应用是解题的关键．
5．C
【分析】
根据，，可得∠CED=∠1，从而∠C=90°，可得①正确；由①可得∠BAD=∠AND，从而∠BAD+∠ADC=180°，又由∠AEB≠∠BAD，可得②错误；根据∠DAE+∠ADE=90°，，且平分，可得∠ADE=∠2，从而得到③正确；由，可得∠EAM+∠EDN=360°-90°=270°，再由和的平分线交于点，可得∠EAF+∠EDF=135°，然后根据四边形的内角和，可得④正确．
【详解】
解：∵，，
∴∠AEB+∠CED=90°，∠1+∠AEB=90°，
∴∠CED=∠1，
∵，
∴∠CED+∠2=90°，
∴∠C=180°-（∠CED+∠2）=90°，
即DC⊥BC，
∴，故①正确；
∴∠BAD=∠ADN，
∵∠ADN+∠ADC=180°，
∴∠BAD+∠ADC=180°，
∵∠AEB≠∠BAD，
∴，故②错误；
∵∠DAE+∠ADE=90°，，且平分，
∴∠ADE=∠2，
∴平分，故③正确；
∵，
∴∠EAM+∠EDN=360°-90°=270°，
∵和的平分线交于点，
∴∠EAF+∠EDF= （∠EAM+∠EDN）=135°，
∵，
∴∠AED=90°，
∴∠F=360°-（∠AED+∠EAF+∠EDF）=135°，故④正确；
故正确的有①③④，共3个，
故选：C．
【点拨】本题主要考查了平行线的判定，角平分线的定义，三角形的内角和与四边形的内角和，熟练掌握相关知识点是解题的关键．
6．B
【分析】
由两直线平行内错角相等求出，再由平分求出，最后由邻补角互补即可求出的度数．
【详解】
解：∵，
∴，
∵平分，
∴，
∴，
故选：B．
【点拨】本题考查了平行线的性质、角平分线的定义、邻补角的概念等，属于基础题，计算过程中细心即可．
7．D
【分析】
由题意易得，则有，然后根据平行线的性质可求解．
【详解】
解：∵，，
∴，
∵平分，
∴，
∴，
∵，
∴；
故选D．
【点拨】本题主要考查平行线的性质及角平分线的定义，熟练掌握平行线的性质及角平分线的定义是解题的关键．
8．A
【分析】
过K作KG//AB，可得KG//CD，可得出两队内错角相等，由EK、FK分别为∠BEF与∠EFD的平分线，再由AB//CD，可以求出∠BEK+∠DFK的度数，即可求出∠EKF的度数，由此类推即可得到∠Kn的度数.
【详解】
解：如图，过K作KG//AB，可得KG//CD，

∴∠BEK＝∠EKG，∠GKF＝∠KFD，
∵EK、FK分别为∠BEF与∠EFD的平分线，
∴∠BEK＝∠FEK，∠EFK＝∠DFK，
∵AB//CD，
∴∠BEK+∠FEK+∠EFK+∠DFK＝180°，即2（∠BEK+∠DFK）＝180°，
∴∠BEK+∠DFK＝90°，
则∠EKF＝∠EKG+∠GKF＝90°；
∵∠BEK、∠DFK的平分线相交于点K1，
∴∠BEK1＝∠KEK1，∠KFK1＝∠DFK1，
∵∠BEK+∠FEK+∠EFK+∠DFK＝180°，即2（∠BEK+∠KFD）＝180°，
∴∠BEK+∠KFD＝90°，即∠KEK1+∠KFK1＝45°，
∴∠K1＝180°﹣（∠KEF+∠EFK）﹣（∠KEK1+∠KFK1）＝×90°＝45°，
同理可得，
归纳总结得：∠Kn＝×90°＝∠EKF．
故选A．
【点拨】本题主要考查了平行线的性质，角平分线的性质，解题的关键在于能够熟练掌握平行线的性质和角平分线的性质.
9．B
【分析】
延长，交于点,根据角平分线的定义以及已知条件可得，由三角形的外角性质可求，最后由平行线的性质即可求解．
【详解】
延长，交于点,

BE平分∠ABD，,
,
,∠DEB＝80°，
,
,
,
故选B．
【点拨】本题考查了角平分线的定义，平行线的性质，三角形的外角性质，掌握以上知识是解题的关键．
10．B
【分析】
先根据平行线的性质可得∠DFG=34°，再根据角平分线的定义可得∠EFD=2∠DFG=68°，然后根据平行线的性质即可得．
【详解】
∵AB//CD,∠FGB=146°，
∴∠DFG=180°−∠FGB=34°，
∵FG平分∠EFD，
∴∠EFD=2∠DFG=68°，
又∵AB//CD，
∴∠AEF=∠EFD=68°，
故选：B．
【点拨】本题考查了平行线的性质、角平分线的定义，熟练掌握平行线的性质是解题关键．
11．D
【分析】
根据对顶角相等求出∠3，再根据两直线平行，同旁内角互补求出∠DFE，然后根据角平分线的定义求出∠DFH，再根据两直线平行，内错角相等解答．
【详解】
解：∵∠1=110°，
∴∠3=∠1=110°，
∵AB∥CD，
∴∠DFE=180°-∠3=180°-110°=70°，
∵HF平分∠EFD，
∴∠DFH=∠DFE=×70°=35°，
∵AB∥CD，
∴∠2=∠DFH=35°．
故选：D．
【点拨】本题考查了平行线的性质，角平分线的定义，对顶角相等的性质，是基础题，熟记各性质并准确识图是解题的关键．
12．C
【分析】
先由两直线平行得到，然后根据角平分线求出∠BEG，再根据两直线平行内交错相等即可得到∠2的值．
【详解】
解：∵，
∴，
∵平分，
∴，
又∵，
∴，
故选：C．
【点拨】本题主要考查了平行线的性质，角平分线的性质，熟练掌握两直线平行内错角相等是解题的关键．
13．A
【分析】
由平行线的性质，得到，由角平分线定义，得到，即可求出的度数．
【详解】
解：∵，，
∴，
∵平分，
∴，
∴的度数是：；
故选：A．
【点拨】本题考查了平行线的性质，角平分线的定义，平角的定义，解题的关键是掌握平行线的性质，正确得到．
14．A
【分析】
延长QP交AB于点G．利用角平分线的性质和平行线的性质，得到∠GQC、∠BGP、∠PEF、∠BEF的相等关系，再利用三角形的外角与内角的关系及平角关系求出∠EGP即可．
【详解】
解：延长QP交AB于点G．

∵EF平分∠PEB，
∴2∠PEF＝2∠BEF＝∠PEB．
∵PQ∥EF，
∴∠BEF＝∠BGP．
∵2∠BEF＋∠GEP＝180°①，
又∵∠EPQ＝∠EGP＋∠GEP，
即∠BEF＋∠GEP＝100°②．
①﹣②，得∠BEF＝∠BGP＝80°．
∵AB∥CD，
∴∠CQP＝∠BGP＝80°．
故选：A．
【点拨】本题考查了平行线的性质、角平分线的性质及三角形的外角与不相邻的内角间关系等知识点，利用2∠BEF＋∠GEP＝180°和∠BEF＋∠GEP＝100°求出∠BGP的度数是解题关键
15．B
【分析】
先利用平行线的性质得到，再根据角平分线得到，最后由直角三角形两锐角互余，即可求解．
【详解】
∵，，
∴ ，
∵平分，
∴,
∵在中，，
∴，
∴
故选：B
【点拨】本题主要考查了平行线的性质，角平分线的定义及直角三角形两锐角的关系，解题的关键是熟练掌握平行线的性质，角平分线的定义及直角三角形两锐角互余．
16．D
【分析】
先根据平行线的性质求出∠DFE的度数，再根据角平分线的定义即可求解．
【详解】
解：∵ABCD，∠FEB=70°，
∴∠EFD=180°-∠FEB=110°，
∵FG是∠EFD的平分线，
∴∠GFD=∠EFD=55°．
故选D．
【点拨】本题考查了平行线的性质，熟练掌握平行线的性质是解答本题的关键．平行线的性质：①两直线平行同位角相等，②两直线平行内错角相等，③两直线平行同旁内角互补．在运用平行线的性质定理时，一定要找准同位角，内错角和同旁内角．
17．已知 3 角平分线的定义 已知 3 等量代换 CD 内错角相等，两直线平行
【分析】
根据平行线证明对书写过程的要求和格式填写即可.
【详解】
证明：∵AC平分∠DAB(已知)，
∴∠1＝∠ 3 (角平分线的定义)，
又∵∠1＝∠2(已知)，
∴∠2＝∠ 3 (等量代换)，
∴AB∥CD (内错角相等，两直线平行)．
故答案为：已知；3；角平分线的定义；已知；3；等量代换；CD；内错角相等，两直线平行
【点拨】本题主要考查平行线证明的书写，正确的逻辑推理和书写格式是解题的关键.
18．②③④
【分析】
①根据同角的余角相等得∠1=∠3，但不一定得45°；②都是根据角平分线的定义、内错角相等，两条直线平行，可得结论；③根据对顶角相等和三角形的外角等于不相邻的两个内角得和，可得结论；④根据三角形内角和定理及同角的余角相等，可得结论．
【详解】
解：①如图，
∵∠CAB=∠DAE=90°，
即∠1+∠2=∠3+∠2+90°，
∴∠1=∠3≠45°，
故①不正确；
②∵AD平分∠CAB，
∴∠1=∠2=45°，
∵∠1=∠3，
∴∠3=45°，
又∵∠C=∠B=45°，
∴∠3=∠B，
∴BC∥AE，
故②正确；
③将三角形ADE绕点A旋转，使得点D落在线段AC上，

则∠4=∠ADE-∠ACB=60°-45°=15°，
故③正确；
④∵∠3=2∠2，∠1=∠3，
∴∠1=2∠2，∠1+∠2=90°，
∴3∠2=90°，
∴∠2=30°，
∴∠3=60°，
又∠E=30°，
设DE与AB交于点F，则∠AFE=90°，
∵∠B=45°，
∴∠4=45°，
∴∠C=∠4，
故④正确，
故答案为：②③④．
【点拨】本题主要考查了同角的余角相等、角平分线定义、平行线的判定的运用，解题关键是熟练掌握同角的余角相等及平行线的判定．
19．70
【分析】
根据平行线性质求出∠CAB的度数，根据角平分线求出∠EAB的度数，再根据平行线性质求出∠AEC的度数即可．
【详解】
解：∵ABCD，
∴∠C+∠CAB=180°，
∵∠C=40°，
∴∠CAB=180°-40°=140°，
∵AE平分∠CAB，
∴∠EAB=70°，
∵ABCD，
∴∠AEC=∠EAB=70°，
故答案为70．
【点拨】本题考查角平分线的定义和平行线的性质，解题的关键是熟练掌握两条平行线被第三条直线所截，同旁内角互补．
20．80°
【分析】
先根据，，得出，可证AD∥BC，再证∠BAD=∠BCD，得出∠AEB=∠F，然后证∠ABC=2∠CBE=2∠F，得出∠ADC=2∠F，利用三角形内角和得出∠CED=180°-∠EDC-∠ECD=180°-2∠F-3∠F=180°-5∠F，根据平角得出∠AEB+∠CED=180°-∠BEC=180°-80°=100°，列方程∠F+180°-5∠F=100°求出∠F=20°即可．
【详解】
解：∵，
∴∠ABC+∠BCD=180°，
∵
∴，
∴AD∥BC，
∵，
∴∠BAD+∠ADC=180°，∠BAF+∠F=180°，
∵∠ADC+∠BCD=180°，
∴∠BAD=∠BCD，
∵，
∴，
∵∠BAF=∠BAD+∠DAF，
∴∠BAF+∠AEB=180°，
∴∠AEB=∠F，
∵AD∥BC，
∴∠CBE=∠AEB，
∵BE平分，
∴∠ABC=2∠CBE=2∠F，
∴∠ADC=2∠F，
∵，
在△CED中，∠CED=180°-∠EDC-∠ECD=180°-2∠F-3∠F=180°-5∠F，
∵，
∴∠AEB+∠CED=180°-∠BEC=180°-80°=100°，
∴∠F+180°-5∠F=100°，
解得∠F=20°，
∴，
故答案为80°．
【点拨】本题考查平行线的判定与性质，三角形内角和，角平分线定义，平角，解一元一次方程，掌握平行线的判定与性质，三角形内角和，角平分线定义，平角，解一元一次方程，关键是证出∠ADC=2∠F．
21．
【分析】
作EF∥AB，证明AB∥ EF∥CD，进而得到∠BED=∠ABE+∠CDE，根据角平分线定义得到，即可求出．
【详解】
解：如图，作EF∥AB，
∵AB∥CD，
∴AB∥ EF∥CD，
∴∠ABE=∠BEF，∠CDE=∠DEF，
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE，
∵BE平分∠ABC，DE平分∠ADC，
∴，
∴ ．

故答案为：
【点拨】本题考查了平行线性质，角平分线的定义，熟知角平分线的性质和平行公理的推论，根据题意添加辅助线是解题关键．
22．20
【分析】
利用角平分线的定义求解再由可得再列方程求解即可.
【详解】
解： BD平分，，

由，
而，

解得：
所以当时，，
故答案为：
【点拨】本题考查的是角平分线的定义，平行线的判定与性质，一元一次方程的应用，掌握平行线的判定与性质是解本题的关键.
23．22.5
【分析】
由平行线的性质可知，由角平分线的定义得，进而可求∠E的度数．
【详解】
解：为正方形，
，，
，
平分，
，
又，
，
故答案为：22.5．
【点拨】本题考查了正方形的性质，平行线的性质，角平分线的定义，熟练掌握正方形的性质是解答本题的关键．
24．40°
【分析】
根据平行线的性质可得∠EAD=∠B，根据角平分线的定义可得∠DAC=∠EAD，即可得答案．
【详解】
∵AD∥BC，∠B＝40°，
∴∠EAD=∠B=40°，
∵AD是∠EAC的平分线，
∴∠DAC=∠EAD=40°，
故答案为：40°
【点拨】本题考查平行线的性质及角平分线的定义，两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；熟练掌握平行线的性质是解题关键．
25．3
【分析】
过点P作PE⊥OB，垂足为E，根据平行线性质，角的平分线性质，得到PE=PD，∠PCE=30°，运用30°角的所对直角边等于斜边的一半计算即可．
【详解】
过点P作PE⊥OB，垂足为E，

∵OP平分∠AOB，∠AOP=15°，PD⊥OA，
∴PD=PE，∠BOP=15°，
∵PC∥OA，
∴∠CPO=∠AOP =15°，
∴∠PCE=30°，
∵PC=6，
∴PE=3，
∴PD=3，
故答案为：3．
【点拨】本题考查了角的平分线定义与性质，平行线的性质，三角形外角和性质，直角三角形的性质，熟练掌握平行线，直角三角形的性质是解题的关键．
26．
【分析】
先过作，根据，得出，再根据平行线的性质，得出，，进而得到；先根据和的平分线交点为，运用图①的结论，得出；同理可得；根据和的平分线，交点为，得出；据此得到规律，最后求得的度数即可．
【详解】
解：如图①，过作，

，
，
，，
，
，
由此可得：
如图②，和的平分线交点为，


，
和的平分线交点为，



，
和的平分线，交点为，



，

以此类推，，
∴，
当时，．
故答案为：．

【点拨】本题主要考查了角平分线的定义以及平行线性质：两直线平行，内错角相等的运用．解决问题的关键是作平行线构造内错角，解题时注意：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
27．①②③
【分析】
根据平行线的性质和∠ABO=40°，由两直线平行，同旁内角互补，可计算出∠BOC的度数，再根据角平分线的性质，可计算出∠BOC的度数，根据角平分线的性质可得出∠BOE的度数，可判断①是否正确．根据OF⊥OE，由∠BOE的度数计算出∠BOF的度数，根据两直线平行，内错角相等的性质，得到∠BOD的度数，可计算出∠3的度数，可得出结论②是否正确，由②中的结论可判断③是否正确．根据平行线的性质，可得到∠OPB=90°，可计算出∠POB的度数，可得出④结论是否正确．
【详解】
解：∵AB∥CD，∠ABO＝40°，
∴∠BOC＝180°﹣∠ABO＝180°﹣40°＝140°，
∵OE平分∠BOC，
∴∠B0E＝∠BOC＝＝70°，
故结论①正确；
∵OF⊥OE，∠B0E＝70°，
∴∠BOF＝90°﹣70°＝20°，
∵AB∥CD，∠ABO＝40°，
∴∠BOD＝∠ABO＝40°，
∴∠FOD＝∠BOD﹣∠BOF＝20°，
∴∠BOF＝∠DOF，
∴OF平分∠BOD，
故结论②正确；
由②的结论可得，
∴∠1＝∠2＝20°，
故结论③正确；
∵OP⊥CD，
∴∠OPB＝90°，
∴∠POB＝90°﹣∠ABO＝50°，
∵2∠3＝2×20°＝40°，
∴∠POB≠2∠3，
故结论④错误．
故答案为：①②③．
【点拨】本题考查了平行线的性质、角平分线性质的应用，合理应用平行线的性质是解决本题关键．
28．35° n°＋35°
【分析】
（1）直接根据角平分线的定义解答即可；
（2）如图，过点E作EF∥AB，然后说明AB∥CD∥EF，再根据平行的性质可得∠BED＝∠FEB＋∠FED＝n°＋35°，最后根据角的和差即可解答．
【详解】
（1）∵DE平分∠ADC，∠ADC＝70°，
∴∠CDE＝∠ADC＝35°，
故填：35°；
（2）如图，过点E作EF∥AB，

∵AB∥CD，
∴AB∥CD∥EF，
∴∠FEB＝∠ABE＝n°，∠FED＝∠CDE＝35°，
∴∠BED＝∠FEB＋∠FED＝n°＋35°，
故填：n°＋35°．
【点拨】本题主要考查了角平分线的定义、平行公理、平行线的性质等知识点，灵活应用平行线的性质成为解答本题的关键．
29．66°
【分析】
先求出∠CDE=12°，再证明AD//BC，求出∠ADC=156°，然后根据角平分线的性质得出∠DAE的度数，即可求得∠DEF的度数．
【详解】
解：∵，
∴∠DCE=∠B=24°，
∵，，
∴∠DCE=2∠CDE=24°，
∴∠CDE=12°，
∵，
∴，
∴AD//BC，
∴∠ADC=∠DCE=24°，∠BAD=180°-24°=156°，
∴∠ADE=24°+12°=36°，
∵AE平分∠BAD，
∴∠DAE=78°，
∴∠DEF=180°-∠DAE-∠ADE=180°-78°-36°=66°．
故答案为：66°．
【点拨】本题考查了平行线的性质与判定，角平分线的定义，能运用平行线的性质进行推理是解此题的关键．
30．
【分析】
根据题意可得，设，分别表示出，进而根据平行线的性质可得∠DFB．
【详解】
∠A＝（60﹣x）°，∠ADC＝（120+x）°，
，
，
，
，
，
BE平分∠CBF，
，
设，
∠DBE＝59°，
，
，
，
，
．
故答案为：．
【点拨】本题考查了平行线的判定与性质，角平分线的定义，证明是解题的关键．
31．①②③．
【分析】
由EG∥BC，且CG⊥EG于G，可得∠GEC＝∠BCA，由CD平分∠BCA，可得∠GEC＝∠BCA＝2∠DCB，可判定①；由CD，BE平分∠BCA，∠ABC，根据外角性质可得∠BFD＝∠BCF+∠CBF＝45°，可判定②；根据同角的余角性质可得∠GCE＝∠ABC，由角的和差∠GCD＝∠ABC+∠ACD=∠ADC，可判定③；由∠GCE+∠ACB＝90°，可得∠GCE与∠ACB互余，可得CA平分∠BCG不正确，可判定④．
【详解】
解:∵EG∥BC，且CG⊥EG于G，
∴∠BCG+∠G＝180°，
∵∠G＝90°，
∴∠BCG＝180°﹣∠G＝90°，
∵GE∥BC，
∴∠GEC＝∠BCA，
∵CD平分∠BCA，
∴∠GEC＝∠BCA＝2∠DCB，
∴①正确．
∵CD，BE平分∠BCA，∠ABC
∴∠BFD＝∠BCF+∠CBF＝（∠BCA+∠ABC）＝45°，
∴②正确．
∵∠GCE+∠ACB＝90°，∠ABC+∠ACB＝90°，
∴∠GCE＝∠ABC，
∵∠GCD＝∠GCE+∠ACD＝∠ABC+∠ACD，∠ADC＝∠ABC+∠BCD，
∴∠ADC＝∠GCD，
∴③正确．
∵∠GCE+∠ACB＝90°，
∴∠GCE与∠ACB互余，
∴CA平分∠BCG不正确，
∴④错误．
故答案为：①②③．
【点拨】本题考查平行线的性质，角平分线定义，垂线性质，角的和差，掌握平行线的性质，角平分线定义，垂线性质，角的和差是解题关键．
32．100
【分析】
根据平行线的性质和角平分线的性质计算即可；
【详解】
解：∵AB∥CE，∠B＝50°，
∴∠ECD＝∠B＝50°，
∵CE平分∠ACD，
∴∠ACD＝2∠ECD＝2×50°＝100°，
故答案为：100．
【点拨】本题主要考查了平行线的性质和角平分线的性质，准确计算是解题的关键．
33．①④
【分析】
①由BC∥OA，∠B=∠A=100°，∠AOB=∠ACB=180°-100°=80°，得到∠A+∠AOB=180°，得出OB∥AC．②OE平分∠BOF，得出∠FOE=∠BOE=∠BOF，∠FOC=∠AOC=∠AOF，从而计算出∠EOC=∠FOE+∠FOC=40°．③由∠OCB=∠AOC，∠OFB=∠AOF=2∠AOC，得出∠OCB：∠OFB=1：2．④由∠OEB=∠OCA=∠AOE=∠BOC，得到∠AOE-∠COE=∠BOC-∠COE，∠BOE=∠AOC，再得到∠BOE=∠FOE=∠FOC=∠AOC=∠AOB=20°，从而计算出∠OCA=∠BOC=3∠BOE=60°．
【详解】
解：∵BC∥OA，∠B=∠A=100°，
∴∠AOB=∠ACB=180°-100°=80°，
∴∠A+∠AOB=180°，
∴OB∥AC．故①正确；
∵OE平分∠BOF，
∴∠FOE=∠BOE=∠BOF，
∴∠FOC=∠AOC=∠AOF，
∴∠EOC=∠FOE+∠FOC=（∠BOF+∠AOF）=×80°=40°．故②错误；
∵∠OCB=∠AOC，∠OFB=∠AOF=2∠AOC，
∴∠OCB：∠OFB=1：2．故③错误；
∵∠OEB=∠OCA=∠AOE=∠BOC，
∴∠AOE-∠COE=∠BOC-∠COE，
∴∠BOE=∠AOC，
∴∠BOE=∠FOE=∠FOC=∠AOC=∠AOB=20°，
∴∠OCA=∠BOC=3∠BOE=60°．故④正确．
故答案为：①④．
【点拨】本题考查了平行线的性质及判定，以及角的计算，熟练掌握平行线的判定与性质是解本题的关键．
34．100°
【分析】
先由同位角相等，证得，进而证得，再由平行线的性质得出与的数量关系，然后由已知条件求得，最后用减去，即可求得答案．
【详解】
解：，







平分，


故答案为：．
【点拨】本题考查了平行线的判定与性质，解题的关键是熟练掌握相关判定定理与性质定理