2021学年2. 相似三角形的判定教课ppt课件

这是一份2021学年2. 相似三角形的判定教课ppt课件，共47页。PPT课件主要包含了相似比是多少，知识回顾，什么叫相似比，新课导入，相似比，相似的表示方法，还可以得到，∵DE∥BC，数学符号语言，练习二等内容，欢迎下载使用。
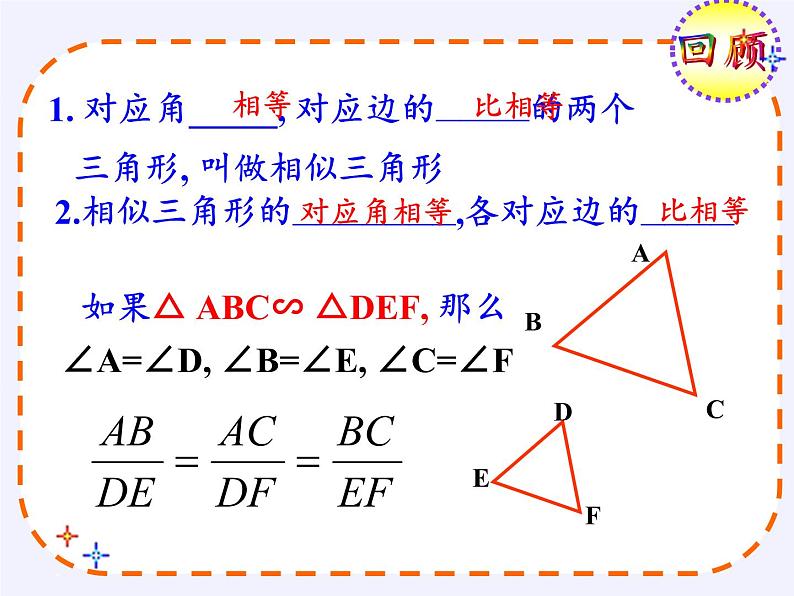
1. 对应角_____, 对应边的————的两个 三角形, 叫做相似三角形
2.相似三角形的———————,各对应边的————
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
１、两个全等三角形一定相似吗？为什么？
２、两个直角三角形一定相似吗？为什么？ 两个等腰直角三角形呢？
３、两个等腰三角形一定相似吗？为什么？ 两个等边三角形呢？
1、相似多边形的性质和判定
3、最简单的相似多边形是什么图形
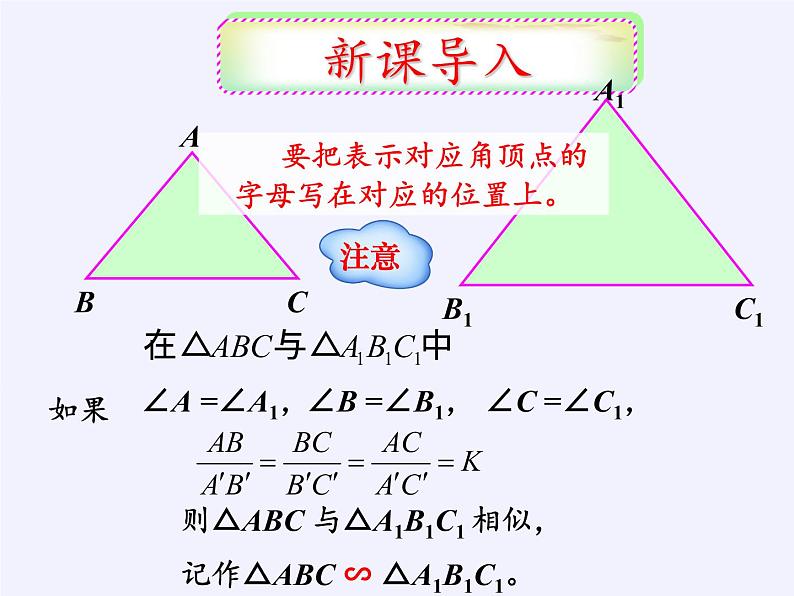
则△ABC 与△A1B1C1 相似，
记作△ABC ∽ △A1B1C1。
要把表示对应角顶点的字母写在对应的位置上。
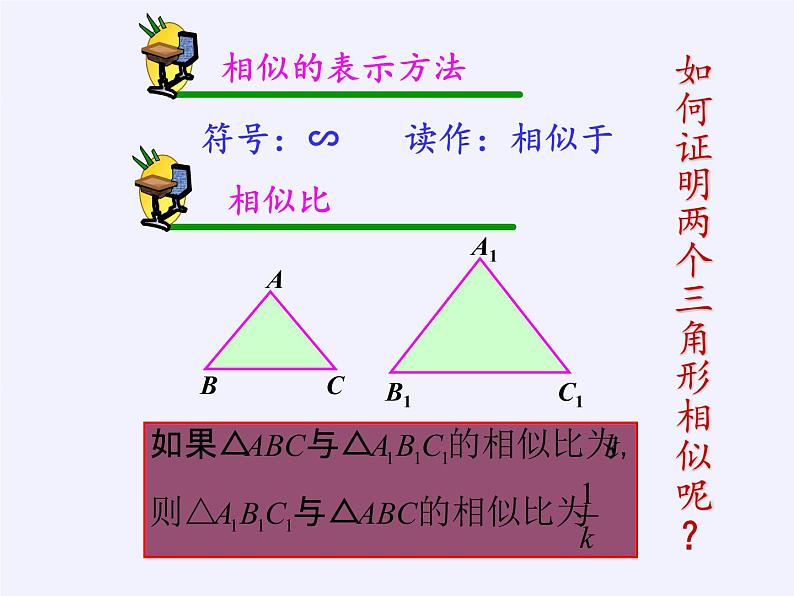
符号：∽ 读作：相似于
如何证明两个三角形相似呢？
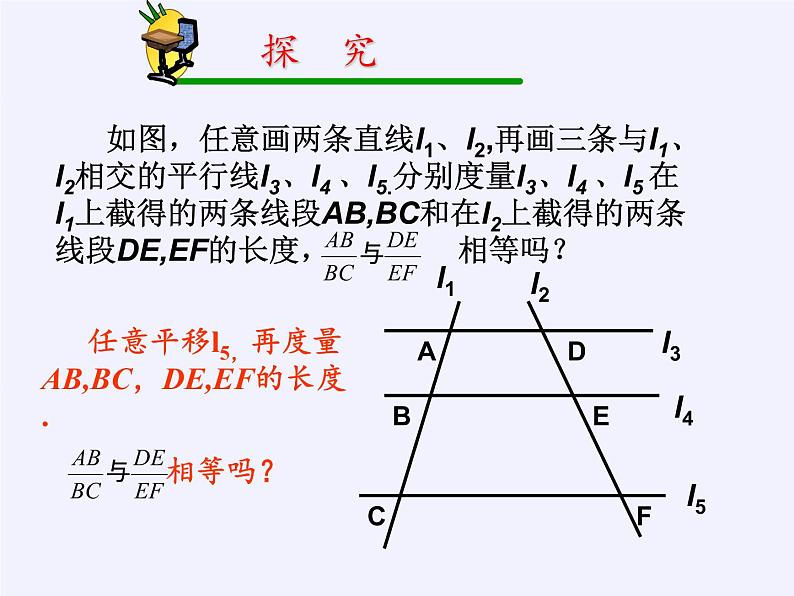
任意平移l5，再度量AB,BC，DE,EF的长度. 相等吗？
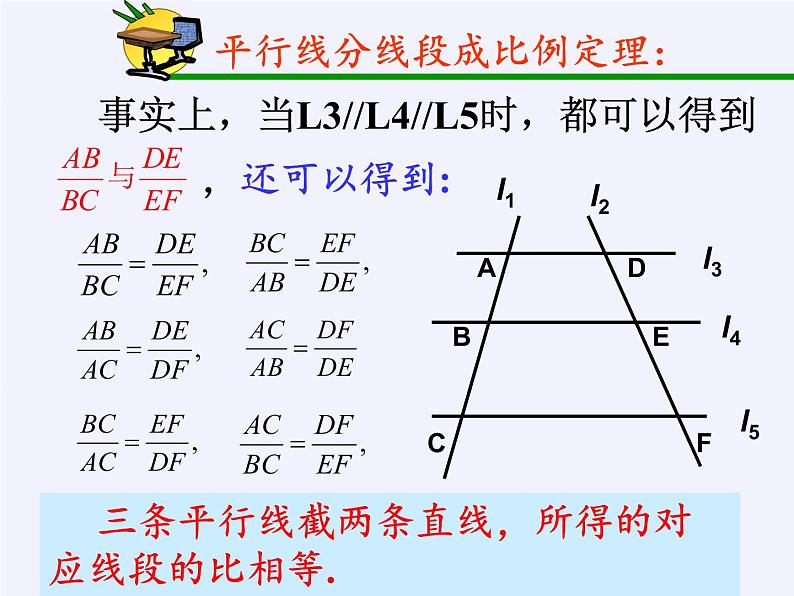
平行线分线段成比例定理：
三条平行线截两条直线，所得的对应线段的比相等.
平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段的比相等.
平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段的比相等
1、如图: 已知 DE∥BC, AB = 14, AC = 18 ， AE = 10，求：AD的长。
1、如图: 已知 DE∥BC, AB = 5, AC = 7 ， AD= 2，求：AE的长。
2、已知 ∠A =∠E=60°求：BD的长。
如图,在△ABC 中,DE//BC,DE分别交AB,AC 于点D,E, △ADE与△ABC有什么关系?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,∵DE//BC,∴∠ADE=∠B, ∠AED=∠C.
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
即:△ADE与△ABC中, ∠A=∠A,∠ADE=∠B, ∠AED=∠C.
相似三角形判定的预备定理
即：在△ABC中，如果DE∥BC，那么△ADE∽△ABC
你还能画出其他图形吗？
平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与三角形相似。
即：如果DE∥BC，那么△ADE∽△ABC
如果再作 MN∥DE ，共有多少对相似三角形？
请写出它们的对应边的比例式
已知：如图，AB∥EF ∥CD，
图中共有____对相似三角形。
△AOB∽ △FOE
如图，△ABC 中，DE∥BC，GF∥AB，DE、ＧＦ交于点Ｏ，则图中与△ABC相似的三角形共有多少个?请你写出来.
解： 与△ABC相似的三角形有3个:　　
△AＤＥ　 △ＧＦＣ　 △ＧＯＥ
如图在平行四边形ABCD中，E为AD上一点，连结CE并延长交BA的延长线于点F，请找出相似的三角形并表示出来。
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm, ∠BAC=450,∠ACB=400. (1)求∠AED和∠ADE的大小;(2)求DE的长.
∠AED=∠C=400.
在△ADE中, ∠ADE=1800-400-450=950.
如图，在△ABC中，DG∥EH∥FI∥BC，（1）请找出图中所有的相似三角形；（2）如果AD=1，DB=3，那么DG：BC=_____。
△ADG∽△AEH∽△AFI∽△ABC
1、如图,在 ABCD中，E是边BC上的一点，且BE:EC=3:2，连接AE、BD交于点F，则BE:AD=_____，BF:FD=_____。
2、如图，在△ABC中，∠C的平分线交AB于D，过点D作DE∥BC交AC于E，若AD:DB=3:2，则EC:BC=______。
4.如图：在△ABC中，点M是BC上任一点， MD∥AC，ME∥AB，
类似于判定三角形全等的方法，我们还能不能通过三边来判断两个三角形相似呢？
是否有△ABC∽△A’B’C’？
已知:如图△ABC和△ 中, 求证:△ABC∽△A`B`C`
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC , ∴
∴ .
因此 .
∴△ ∽△ABC
要证明△ABC∽△A’B’C’，可以先作一个与△ABC全等的三角形，证明它△A’B’C’与相似．这里所作的三角形是证明的中介，它把△ABC△A’B’C’联系起来．
△ABC∽△A’B’C’
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边对应的比相等,两三角形相似.
三角形相似判定定理之一
求证：∠BAD=∠CAE。
∴ΔABC∽ΔADE∴∠BAC=∠DAE∴∠BAC－∠DAC =∠DAE－∠DAC即∠BAD=∠CAE
　　类似于判定三角形全等的方法，我们能通过两边和夹角来判断两个三角形相似呢？
　　实际上，我们有利用两边和夹角判定两个三角形相似的方法．
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角相似.
对于△ABC和△A’B’C’, 如果 ,∠B=∠B’,这两个三角形一定相似吗?试着画画看.
例1:根据下列条件，判断△ABC与△A’B’C’是否相似，并说明理由．(1)∠A=1200,AB=7cm,AC=14cm.∠A’=1200,A’B’=3cm,A’C’=6cm.(2)AB=4 cm,BC=6cm,AC=8cm,A’B’=12cm,B’C’=18cm,A’C’=21cm.
△ABC与△A’B’C‘的三组对应边的比不等，它们不相似．
要使两三角形相似，不改变的AC长，A’C’的长应改为多少？
1.根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由:
(1)∠A=400,AB=8,AC=15, ∠A’=400,A’B’=16,A’C’=30;
(2)AB=10cm,BC=8cm,AC=16cm,A’B’=16cm,B’C’=12.8cm,A’C’=25.6cm.
2.图中的两个三角形是否相似?
4:2=5:x=6:y4:x=5:2=6:y4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?
 平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似;
 两边对应成比例且夹角相等,两三角形相似.
 三边对应成比例,两三角形相似.