2020-2021学年3. 相似三角形的性质说课ppt课件

这是一份2020-2021学年3. 相似三角形的性质说课ppt课件，共19页。PPT课件主要包含了比一比，二往事新忆，新知猜想，填一填，随堂练习，你的收获是什么等内容，欢迎下载使用。
我相似三角形的性质 最多！
我全等三角形的性质最简单！
小兔说：全等三角形的对应边对应角相等，对应边上的高相等，对应边上的中线相等，还有对应角的角平分线也相等。
大象说：我也知道相似三角形的对应边成比例，对应角相等啊！对应边上的高？对应边上中线？对应角的角平分线？有什么关系呢？
1. 相似三角形的判定方法：
1.定义：三边对应成比例三角相等
4.两边成比例且夹角相等
对应角相等， 对应边成比例 相似三角形还有哪些性质？
2. 相似三角形的性质：
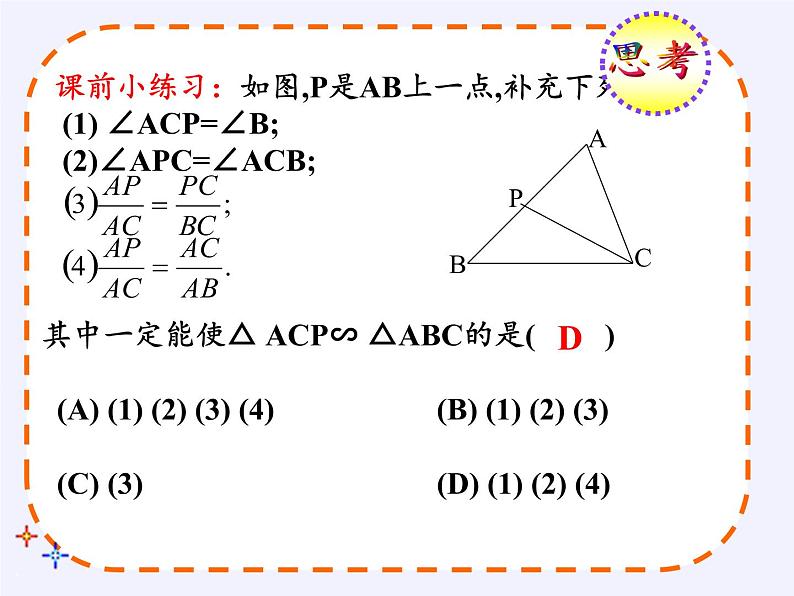
课前小练习：如图,P是AB上一点,补充下列条件: (1) ∠ACP=∠B; (2)∠APC=∠ACB;
其中一定能使△ ACP∽ △ABC的是( ) (A) (1) (2) (3) (4) (B) (1) (2) (3) (C) (3) (D) (1) (2) (4)
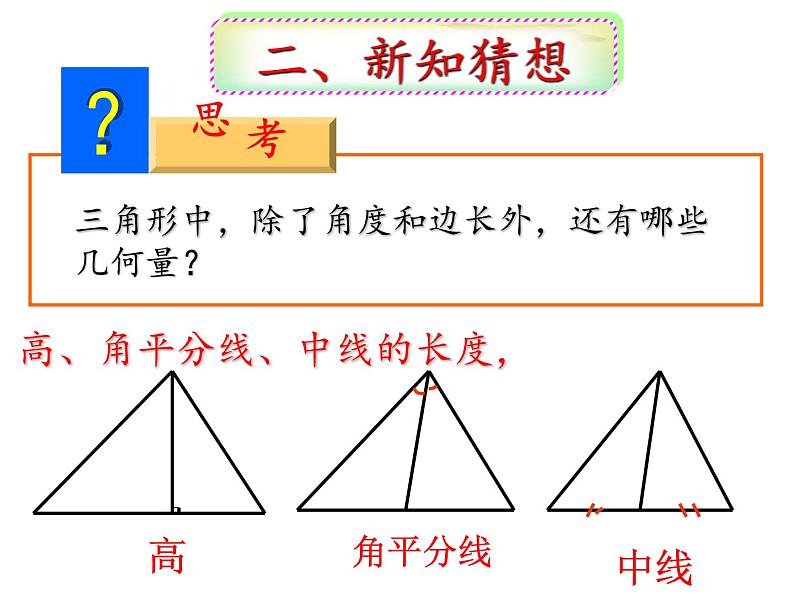
三角形中，除了角度和边长外，还有哪些几何量？
高、角平分线、中线的长度，
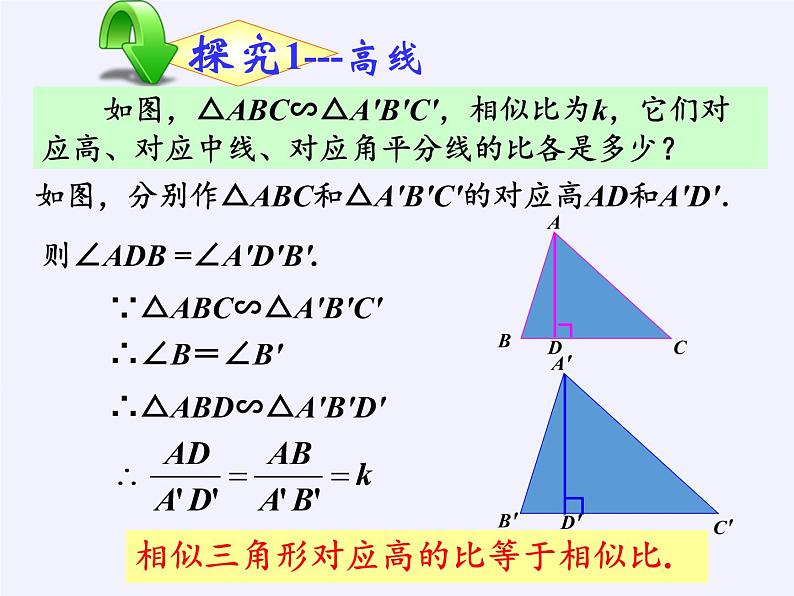
如图，△ABC∽△A'B'C'，相似比为k，它们对应高、对应中线、对应角平分线的比各是多少？
如图，分别作△ABC和△A'B'C'的对应高AD和A'D'．
则∠ADB =∠A'D'B'.
∵△ABC∽△A'B'C'
∴△ABD∽△A'B'D'
相似三角形对应高的比等于相似比.
如图，分别作△ABC和△ A'B'C'的对应中线AE和A'E'，
你能类比前面的方法证明吗？
相似三角形对应中线的比等于相似比.
如图，分别作△ABC和△ A'B'C'的对应角平分线AF和A'F'．
相似三角形对应角平分线的比等于相似比.
相似三角形对应线段的比等于相似比.
相似三角形对应高的比，对应中线的比，对应角平分线的比都等于相似比.
通过前面的思考、探索、推理，我们得到相似三角形有如下性质；
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
例1：已知△ABC∽ △A´B ´C ´，BD和B ´D ´分别是△ABC和△A´B´C´中线，且AB＝10，A´B´＝2，BD＝6。求B´D´的长。
解：∵　△ABC∽△A´B´C´
答：B´D´的长为1.2。
例2：已知△ABC∽△DEF，BG、EH分别是△ABC和 △DEF的角平分线，BC＝6cm,EF＝4cm,BG＝4.8cm.求EH的长。
解：∵ △ABC∽△DEF 　
∴　BC∶EF＝BG∶EH
答：EH的长为3.2cm。
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2．两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________.
3、已知△ABC∽△A´B´C´，AD、A ´D ´分别是对应边BC、B ´C ´上的高，若BC＝8cm,B ´C ´＝6cm,AD＝4cm,则A ´D ´等于（ ）A 16cm B 12 cm C 3 cm D 6 cm
4、两个相似三角形对应高的比为3∶7，它们的对应角平分线的比为（ ）A 7∶3 B 49∶9 C 9∶49 D 3∶7
相似三角形的性质①相似三角形的对应角相等,对应边成比例.②相似三角形对应中线的比,对应角平分线的比，对应高的比,都等于相似比.