初中数学华师大版九年级上册23.4 中位线课前预习ppt课件

这是一份初中数学华师大版九年级上册23.4 中位线课前预习ppt课件，共13页。PPT课件主要包含了平方厘米，解连结AO，连结BD，平行四边形，DF互相平分，思考题等内容，欢迎下载使用。

1、认识三角形的中位线，会画三角形的中位线；
2、理解三角形的中位线性质，会用中位线性质去解决相关问题；
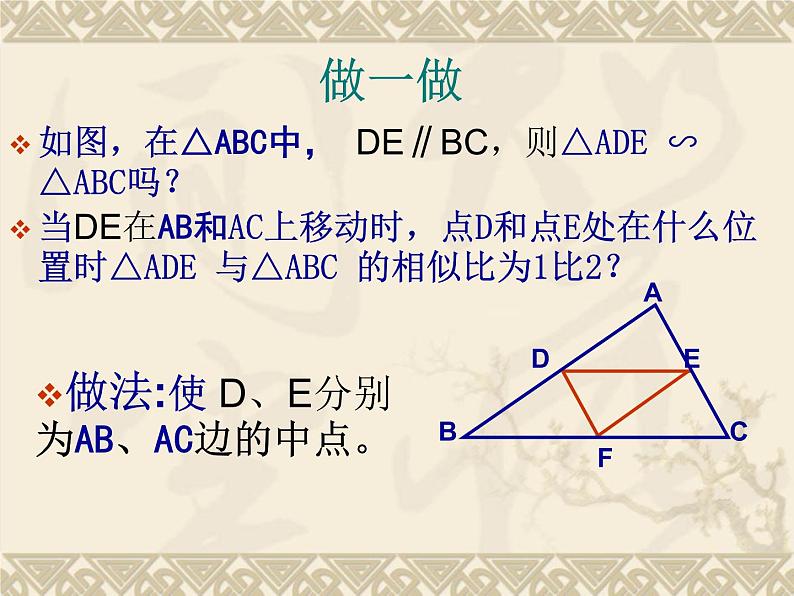
如图，在△ABC中， DE∥BC，则△ADE ∽ △ABC吗？当DE在AB和AC上移动时，点D和点E处在什么位置时△ADE 与△ABC 的相似比为1比2？
做法:使 D、E分别为AB、AC边的中点。
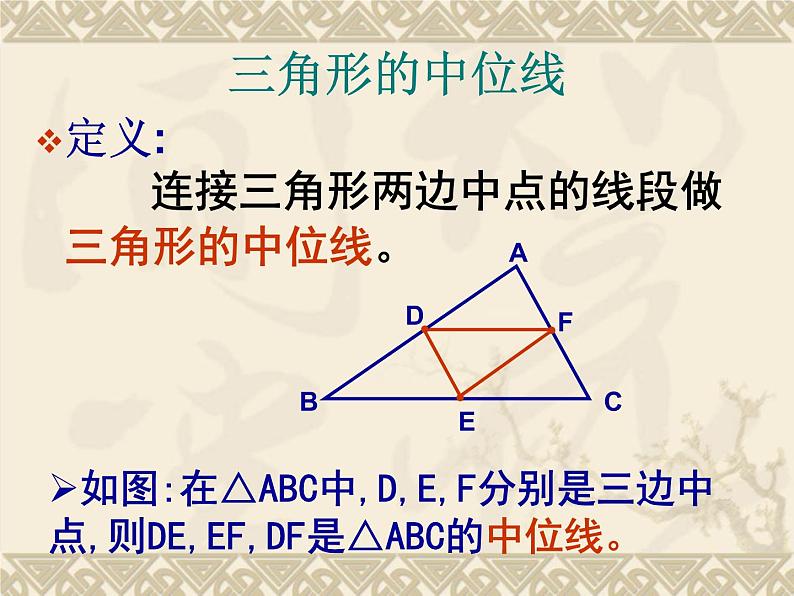
定义: 连接三角形两边中点的线段做三角形的中位线。
如图:在△ABC中,D,E,F分别是三边中点,则DE,EF,DF是△ABC的中位线。
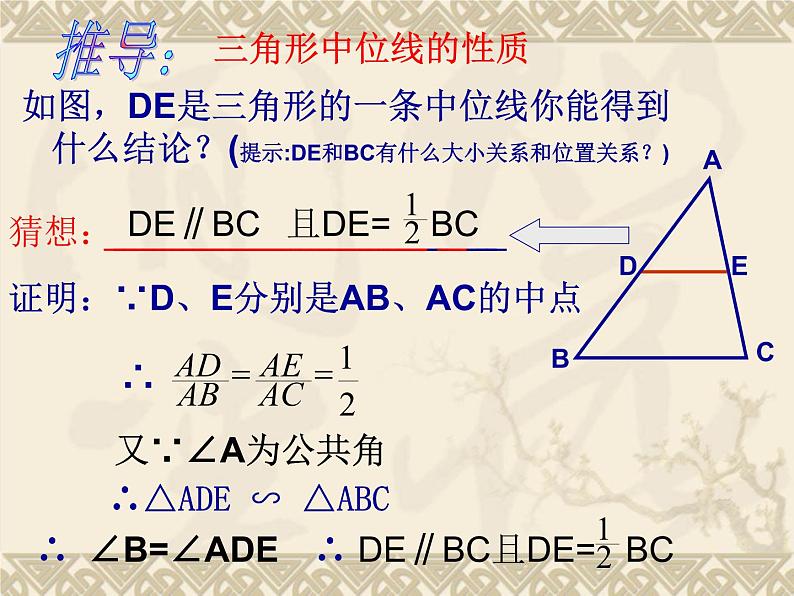
如图，DE是三角形的一条中位线你能得到什么结论？(提示:DE和BC有什么大小关系和位置关系？)
猜想：̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲ ̲
DE∥BC且DE= BC
证明：∵D、E分别是AB、AC的中点
∴△ADE ∽ △ABC
∴ DE∥BC且DE= BC
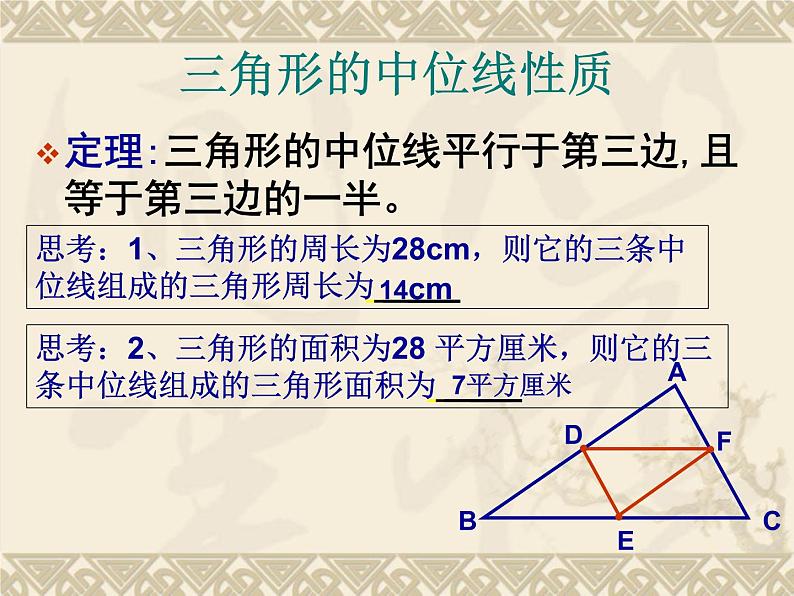
定理:三角形的中位线平行于第三边,且等于第三边的一半。
思考：1、三角形的周长为28cm，则它的三条中位线组成的三角形周长为̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲̲
思考：2、三角形的面积为28 平方厘米，则它的三条中位线组成的三角形面积为̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲̲
1、已知BD、CE是△ABC的中线，相交于O点，F、G分别是BO、CO的中点，求证：EF平行且等于DG
∵ BD、CE是△ABC的中线 F、G分别是BO、CO的中点
∴ EF∥OA GD∥OA EF= OA GD= OA
∴ EF= DG且EF∥ GD
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新四边形的形状有什么特征?
FG∥BD且FG= BD
四边形EFGH是平行四边形
∴ EH∥FG且EH= FG
∴四边形EHGF是平形四边形
∵ EH∥BD且EH= BD
1、平行四边形各边中点围成的四边形是̲ ̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲̲ 2、矩形各边中点围成的四边形是̲ ̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲3、菱形各边中点围成的四边形是̲ ̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲4、正方形各边中点围成的四边形是̲ ̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲5、等腰梯形各边中点围成的四边形是̲ ̲ ̲ ̲ ̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲̲ ̲ ̲
6、任意四边形各边中点围成的四边形是
2、求证三角形的一条中位线与第三边的中线互相平分
已知：如图所示，在△ABC中AD=DB，AF=FC，BE=EC
求证：AE、DF互相平分
∵ D、E、F分别为AB、BC、AC上中点
∴DE、EF为△ABC的中位线
DE ∥ AF、AD ∥EF
四边形ADEF是
如图所示， △ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G，求证：
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半。
任意四边形四边中点连线所组成的四边形是：平行四边行